W rozkładzie normalnym dane są symetrycznie rozłożone bez przechylenia. Po naniesieniu na wykres, dane mają kształt dzwonu, z większością wartości skupionych wokół centralnego regionu i zmniejszających się w miarę oddalania się od centrum.
Rozkłady normalne są również nazywane rozkładami gaussowskimi lub krzywymi dzwonowymi ze względu na ich kształt.

- Dlaczego rozkłady normalne mają znaczenie?
- Jakie są właściwości rozkładów normalnych?
- Jaki jest Twój wynik plagiatu?
- Empirical rule
- Twierdzenie o granicach centralnych
- Formuła krzywej normalnej
- Co to jest standardowy rozkład normalny?
- Odnajdywanie prawdopodobieństwa przy użyciu rozkładu z
- Często zadawane pytania dotyczące rozkładów normalnych
Dlaczego rozkłady normalne mają znaczenie?
Wszystkie rodzaje zmiennych w naukach przyrodniczych i społecznych mają rozkład normalny lub w przybliżeniu normalny. Wzrost, waga urodzeniowa, umiejętność czytania, satysfakcja z pracy lub wyniki SAT są tylko kilkoma przykładami takich zmiennych.
Ponieważ normalnie rozłożone zmienne są tak powszechne, wiele testów statystycznych jest zaprojektowanych dla normalnie rozłożonych populacji.
Zrozumienie właściwości rozkładów normalnych oznacza, że możesz używać statystyki wnioskowania do porównywania różnych grup i dokonywania szacunków na temat populacji przy użyciu próbek.
Jakie są właściwości rozkładów normalnych?
Rozkłady normalne mają kluczowe cechy, które łatwo zauważyć na wykresach:
- Średnia, mediana i tryb są dokładnie takie same.
- Rozkład jest symetryczny względem średniej – połowa wartości jest poniżej średniej, a połowa powyżej średniej.
- Rozkład może być opisany przez dwie wartości: średnią i odchylenie standardowe.


Średnia jest parametrem położenia, podczas gdy odchylenie standardowe jest parametrem skali.
Średnia określa, gdzie szczyt krzywej jest wyśrodkowany. Zwiększenie średniej powoduje przesunięcie krzywej w prawo, natomiast jej zmniejszenie powoduje przesunięcie krzywej w lewo.


Odchylenie standardowe rozciąga lub ściska krzywą. Małe odchylenie standardowe skutkuje wąską krzywą, natomiast duże odchylenie standardowe prowadzi do szerokiej krzywej.


Empirical rule
Reguła empiryczna, lub reguła 68-95-99.7 rule, tells you where most of your values lie in a normal distribution:
- Around 68% of values are within 1 standard deviation from the mean.
- Around 95% of values are within 2 standard deviations from the mean.
- Around 99.7% of values are within 3 standard deviations from the mean.
Postępując zgodnie z regułą empiryczną:
- Około 68% wyników znajduje się pomiędzy 1000 i 1300, 1 odchylenie standardowe powyżej i poniżej średniej.
- Około 95% wyników znajduje się pomiędzy 850 a 1450, 2 odchylenia standardowe powyżej i poniżej średniej.
- Około 99,7% wyników znajduje się pomiędzy 700 a 1600, 3 odchylenia standardowe powyżej i poniżej średniej.


Reguła empiryczna jest szybkim sposobem na zorientowanie się w danych i sprawdzenie, czy nie ma wartości odstających lub ekstremalnych, które nie podążają za tym wzorcem.
Jeśli dane z małych próbek nie podążają ściśle za tym wzorcem, inne rozkłady, takie jak rozkład t, mogą być bardziej odpowiednie. Po zidentyfikowaniu rozkładu zmiennej, można zastosować odpowiednie testy statystyczne.
Twierdzenie o granicach centralnych
Twierdzenie o granicach centralnych jest podstawą tego, jak rozkłady normalne działają w statystyce.
W badaniach, aby uzyskać dobre pojęcie o średniej populacji, idealnie byłoby zebrać dane z wielu losowych próbek w obrębie populacji. Rozkład próbkowy średniej jest rozkładem średnich z tych różnych próbek.
Twierdzenie o granicach centralnych pokazuje, co następuje:
- Prawo wielkich liczb: Wraz ze wzrostem wielkości próbki (lub liczby próbek), wtedy średnia z próbki zbliży się do średniej populacji.
- Przy wielu dużych próbkach, rozkład próbkowania średniej jest normalnie rozłożony, nawet jeśli twoja oryginalna zmienna nie jest normalnie rozłożona.
Parametryczne testy statystyczne zazwyczaj zakładają, że próbki pochodzą z normalnie rozłożonych populacji, ale centralne twierdzenie graniczne oznacza, że to założenie nie jest konieczne do spełnienia, gdy masz wystarczająco dużą próbkę.
Możesz użyć testów parametrycznych dla dużych próbek z populacji o dowolnym rozkładzie, tak długo jak inne ważne założenia są spełnione. Wielkość próbki 30 lub więcej jest ogólnie uważana za dużą.
Dla małych próbek, założenie normalności jest ważne, ponieważ rozkład próbkowania średniej nie jest znany. Aby uzyskać dokładne wyniki, musisz mieć pewność, że populacja jest normalnie rozłożona, zanim będziesz mógł użyć testów parametrycznych z małymi próbkami.
Formuła krzywej normalnej
Gdy masz już średnią i odchylenie standardowe rozkładu normalnego, możesz dopasować krzywą normalną do swoich danych za pomocą funkcji gęstości prawdopodobieństwa.


W funkcji gęstości prawdopodobieństwa obszar pod krzywą mówi nam o prawdopodobieństwie. Rozkład normalny jest rozkładem prawdopodobieństwa, więc całkowity obszar pod krzywą zawsze wynosi 1 lub 100%.
Wzór na normalną funkcję gęstości prawdopodobieństwa wygląda na dość skomplikowany. Ale aby go użyć, wystarczy znać średnią populacji i odchylenie standardowe.
Dla dowolnej wartości x, można wstawić średnią i odchylenie standardowe do wzoru, aby znaleźć gęstość prawdopodobieństwa zmiennej przyjmującej tę wartość x.
| Normalny wzór na gęstość prawdopodobieństwa | Wyjaśnienie |
|---|---|
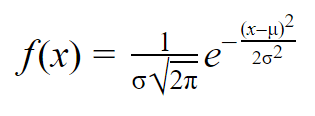 |
|
Na twoim wykresie funkcji gęstości prawdopodobieństwa prawdopodobieństwo jest zacienionym obszarem pod krzywą, który leży na prawo od miejsca, w którym twoje wyniki SAT są równe 1380.


Możesz znaleźć wartość prawdopodobieństwa tego wyniku, używając standardowego rozkładu normalnego.
Co to jest standardowy rozkład normalny?
Standardowy rozkład normalny, zwany również rozkładem z, jest specjalnym rozkładem normalnym, w którym średnia wynosi 0, a odchylenie standardowe 1.
Każdy rozkład normalny jest wersją standardowego rozkładu normalnego, który został rozciągnięty lub ściśnięty i przesunięty poziomo w prawo lub w lewo.


Podczas gdy pojedyncze obserwacje z rozkładów normalnych są określane jako x, są one określane jako z w rozkładzie z. Każdy rozkład normalny można przekształcić w standardowy rozkład normalny, zamieniając poszczególne wartości na z-współczynniki.
Z-współczynniki mówią, ile odchyleń standardowych od średniej leży każda wartość.


Trzeba znać tylko średnią i odchylenie standardowe rozkładu, aby znaleźć z-score danej wartości.
| Wzór na Z-score | Wyjaśnienie |
|---|---|
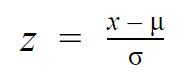 |
|
Z kilku powodów przekształcamy rozkłady normalne w standardowy rozkład normalny:
- Aby znaleźć prawdopodobieństwo, że obserwacje w rozkładzie wypadną powyżej lub poniżej danej wartości.
- Aby znaleźć prawdopodobieństwo, że średnia z próby znacząco różni się od znanej średniej populacji.
- Aby porównać wyniki na różnych rozkładach o różnych średnich i odchyleniach standardowych.
Odnajdywanie prawdopodobieństwa przy użyciu rozkładu z
Każdy wynik z jest związany z prawdopodobieństwem, lub wartością p, która mówi o prawdopodobieństwie wystąpienia wartości poniżej tego wyniku z. Jeśli przekształcisz indywidualną wartość w z-score, możesz znaleźć prawdopodobieństwo wystąpienia wszystkich wartości do tej wartości w rozkładzie normalnym.
Średnia naszego rozkładu wynosi 1150, a odchylenie standardowe 150. Wynik z-score mówi nam, ile odchyleń standardowych dzieli 1380 od średniej.
| Formuła | Obliczenia |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
Dla z-score równego 1.53, wartość p wynosi 0.937. Jest to prawdopodobieństwo, że wynik SAT wynosi 1380 lub mniej (93,7%), i jest to obszar pod krzywą na lewo od zacieniowanego obszaru.


Aby znaleźć zacieniowany obszar, należy odjąć 0.937 od 1, który jest całkowitym obszarem pod krzywą.
Prawdopodobieństwo x>1380 = 1 – 0,937 = 0,063
To oznacza, że jest prawdopodobne, że tylko 6,3% wyników SAT w twojej próbie przekracza 1380.
Często zadawane pytania dotyczące rozkładów normalnych
W rozkładzie normalnym, dane są symetrycznie rozłożone bez skośności. Większość wartości skupia się wokół centralnego regionu, a wartości zmniejszają się w miarę oddalania się od centrum.
Miary tendencji centralnej (średnia, tryb i mediana) są dokładnie takie same w rozkładzie normalnym.
Standardowy rozkład normalny, zwany również rozkładem z, jest specjalnym rozkładem normalnym, w którym średnia wynosi 0, a odchylenie standardowe 1.
Każdy rozkład normalny może być przekształcony w standardowy rozkład normalny przez przekształcenie poszczególnych wartości w z-rozkłady. W rozkładzie z, z-scores mówią ile odchyleń standardowych od średniej leży każda wartość.
Reguła empiryczna lub reguła 68-95-99,7 mówi, gdzie leży większość wartości w rozkładzie normalnym:
- Około 68% wartości znajduje się w granicach 1 odchylenia standardowego od średniej.
- Około 95% wartości znajduje się w granicach 2 odchyleń standardowych od średniej.
- Około 99,7% wartości mieści się w 3 odchyleniach standardowych od średniej.
Reguła empiryczna jest szybkim sposobem na uzyskanie przeglądu danych i sprawdzenie, czy nie ma wartości odstających lub skrajnych, które nie podążają za tym wzorcem.
Rozkład t jest sposobem opisania zbioru obserwacji, w którym większość obserwacji znajduje się blisko średniej, a pozostałe obserwacje tworzą ogony po obu stronach. Jest to rodzaj rozkładu normalnego używanego w przypadku mniejszej liczebności próby, gdy wariancja danych jest nieznana.
Rozkład t tworzy krzywą dzwonową, gdy jest naniesiony na wykres. Można go opisać matematycznie za pomocą średniej i odchylenia standardowego.
.

