El resultado en el análisis de regresión logística suele codificarse como 0 o 1, donde 1 indica que el resultado de interés está presente, y 0 indica que el resultado de interés está ausente. Si definimos p como la probabilidad de que el resultado sea 1, el modelo de regresión logística múltiple puede escribirse como sigue:
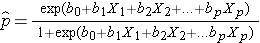
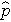es la probabilidad esperada de que el resultado esté presente; X1 a Xp son variables independientes distintas; y b0 a bp son los coeficientes de regresión. El modelo de regresión logística múltiple se escribe a veces de forma diferente. En la siguiente forma, el resultado es el logaritmo esperado de las probabilidades de que el resultado esté presente,
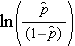
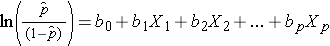
Nótese que el lado derecho de la ecuación anterior se parece a la ecuación de regresión lineal múltiple. Sin embargo, la técnica para estimar los coeficientes de regresión en un modelo de regresión logística es diferente de la utilizada para estimar los coeficientes de regresión en un modelo de regresión lineal múltiple. En la regresión logística, los coeficientes derivados del modelo (por ejemplo, b1) indican el cambio en las probabilidades logarítmicas esperadas en relación con un cambio de una unidad en X1, manteniendo todos los demás predictores constantes. Por lo tanto, el antilog de un coeficiente de regresión estimado, exp(bi), produce una razón de probabilidades, como se ilustra en el ejemplo siguiente.
Ejemplo de regresión logística – Asociación entre obesidad y ECV
Previamente analizamos los datos de un estudio diseñado para evaluar la asociación entre la obesidad (definida como IMC > 30) y la enfermedad cardiovascular incidente. Se recopilaron datos de participantes con edades comprendidas entre los 35 y los 65 años, y libres de enfermedad cardiovascular (ECV) al inicio del estudio. Se realizó un seguimiento de cada participante durante 10 años para detectar el desarrollo de enfermedades cardiovasculares. En la página 2 de este módulo se puede encontrar un resumen de los datos. El riesgo relativo no ajustado o bruto fue RR = 1,78, y la odds ratio no ajustada o bruta fue OR =1,93. También determinamos que la edad era un factor de confusión, y utilizando el método de Cochran-Mantel-Haenszel, estimamos un riesgo relativo ajustado de RRCMH =1,44 y una odds ratio ajustada de ORCMH =1,52. Ahora utilizaremos el análisis de regresión logística para evaluar la asociación entre la obesidad y la enfermedad cardiovascular incidente ajustando por edad.
El análisis de regresión logística revela lo siguiente:
|
Variable independiente |
Coeficiente de regresión |
Chi-cuadrado |
Valor P |
|---|---|---|---|
|
Intercepción |
-2.367 |
307.38 |
0.0001 |
|
Obesidad |
0,658 |
9,87 |
0.0017 |
El modelo de regresión logística simple relaciona la obesidad con las probabilidades logarítmicas de ECV incidente:
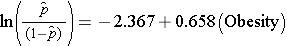
La obesidad es una variable indicadora en el modelo, codificada como sigue: 1=obeso y 0=no obeso. La probabilidad logarítmica de sufrir una ECV es 0,658 veces mayor en las personas obesas que en las no obesas. Si tomamos el antilog del coeficiente de regresión, exp(0,658) = 1,93, obtenemos la odds ratio cruda o no ajustada. Las probabilidades de desarrollar una ECV son 1,93 veces mayores entre las personas obesas en comparación con las no obesas. La asociación entre la obesidad y la ECV incidente es estadísticamente significativa (p=0,0017). Obsérvese que los estadísticos de prueba para evaluar la importancia de los parámetros de regresión en el análisis de regresión logística se basan en los estadísticos chi-cuadrado, a diferencia de los estadísticos t, como en el caso del análisis de regresión lineal. Esto se debe a que se utiliza una técnica de estimación diferente, llamada estimación de máxima verosimilitud, para estimar los parámetros de regresión (véase Hosmer y Lemeshow3 para los detalles técnicos).
Muchos paquetes informáticos estadísticos también generan odds ratios así como intervalos de confianza del 95% para los odds ratios como parte de su procedimiento de análisis de regresión logística. En este ejemplo, la estimación de la odds ratio es 1,93 y el intervalo de confianza del 95% es (1,281, 2,913).
Al examinar la asociación entre la obesidad y la ECV, determinamos previamente que la edad era un factor de confusión.El siguiente modelo de regresión logística múltiple estima la asociación entre la obesidad y la ECV incidente, ajustando por edad. En el modelo volvemos a considerar dos grupos de edad (menores de 50 años y mayores de 50 años). Para el análisis, el grupo de edad se codifica como sigue: 1=50 años o más y 0=menos de 50 años.
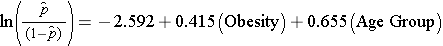
Si tomamos el antilog del coeficiente de regresión asociado a la obesidad, exp(0,415) = 1,52 obtenemos la odds ratio ajustada por edad. Las probabilidades de desarrollar una ECV son 1,52 veces mayores entre las personas obesas en comparación con las no obesas, ajustando por edad. En la sección 9.2 utilizamos el método Cochran-Mantel-Haenszel para generar una odds ratio ajustada por edad y encontramos lo siguiente:
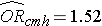
Esto ilustra cómo el análisis de regresión logística múltiple puede utilizarse para tener en cuenta los factores de confusión. Los modelos pueden ampliarse para tener en cuenta varias variables de confusión simultáneamente. El análisis de regresión logística múltiple también puede utilizarse para evaluar la confusión y la modificación del efecto, y los enfoques son idénticos a los utilizados en el análisis de regresión lineal múltiple. El análisis de regresión logística múltiple también puede utilizarse para examinar el impacto de múltiples factores de riesgo (en lugar de centrarse en un único factor de riesgo) en un resultado dicotómico.
Ejemplo – Factores de riesgo asociados con el bajo peso del bebé al nacer
Supongamos que los investigadores también están preocupados por los resultados adversos del embarazo, incluyendo la diabetes gestacional, la preeclampsia (es decir, la hipertensión inducida por el embarazo) y el parto prematuro. Recordemos que en el estudio participaron 832 mujeres embarazadas que proporcionaron datos demográficos y clínicos. En la muestra del estudio, 22 (2,7%) mujeres desarrollan preeclampsia, 35 (4,2%) desarrollan diabetes gestacional y 40 (4,8%) desarrollan parto prematuro. Supongamos que deseamos evaluar si existen diferencias en cada uno de estos resultados adversos del embarazo por raza/etnia, ajustados por la edad materna. Se realizaron tres análisis de regresión logística por separado que relacionaban cada resultado, considerado por separado, con las 3 variables ficticias o indicadores que reflejan la raza de la madre y su edad, en años. Los resultados son los siguientes.
|
Resultado: Preeclampsia |
Coeficiente de regresión |
Chi-cuadrado |
Valor P |
Razón de probabilidades (IC 95%) |
|---|---|---|---|---|
|
Intercepción |
-3.066 |
4.518 |
0.0335 |
– |
|
Raza negra |
2,191 |
12,640 |
0,0004 |
8.948 (2,673, 29,949) |
|
Raza hispana |
-0,1053 |
0,0325 |
0,8570 |
0.900 (0,286, 2,829) |
|
Otra raza |
0,0586 |
0,0021 |
0.9046 |
1,060 (0,104, 3,698) |
|
Edad de las madres (años) |
-0,0252 |
0.3574 |
0,5500 |
0,975 (0,898, 1,059) |
La única diferencia estadísticamente significativa en cuanto a la preeclampsia se da entre las madres negras y las blancas.
Las madres negras tienen casi 9 veces más probabilidades de desarrollar preeclampsia que las blancas, ajustadas por la edad materna. El intervalo de confianza del 95% para el odds ratio que compara a las mujeres negras con las blancas que desarrollan preeclampsia es muy amplio (2,673 a 29,949). Esto se debe al hecho de que hay un pequeño número de eventos de resultado (sólo 22 mujeres desarrollan preeclampsia en la muestra total) y un pequeño número de mujeres de raza negra en el estudio. Por lo tanto, esta asociación debe interpretarse con precaución.
Si bien el odds ratio es estadísticamente significativo, el intervalo de confianza sugiere que la magnitud del efecto podría ser desde un aumento de 2,6 veces hasta un aumento de 29,9 veces. Se necesita un estudio más amplio para generar una estimación más precisa del efecto.
|
Diabetes gestacional |
Coeficiente de regresión |
Chi-cuadrado |
Valor P |
Razón de probabilidades (IC 95%) |
|---|---|---|---|---|
|
Intercepción |
-5.823 |
22,968 |
0,0001 |
– |
|
Raza negra |
1,621 |
6.660 |
0,0099 |
5,056 (1,477, 17,312) |
|
Raza hispana |
0,581 |
1.766 |
0,1839 |
1,787 (0,759, 4,207) |
|
Otra raza |
1,348 |
5.917 |
0,0150 |
3,848 (1,299, 11,395) |
|
Edad de la madre (años) |
0,071 |
4.314 |
0,0378 |
1,073 (1,004, 1,147) |
Con respecto a la diabetes gestacional, existen diferencias estadísticamente significativas entre las madres negras y las blancas (p=0,0099) y entre las madres que se identifican como de otra raza en comparación con las blancas (p=0,0150), ajustadas por la edad de la madre. La edad de la madre también es estadísticamente significativa (p=0,0378), siendo las mujeres de mayor edad más propensas a desarrollar diabetes gestacional, ajustado por raza/etnia.
|
Resultado: Parto prematuro |
Coeficiente de regresión |
Chi-cuadrado |
Valor P |
Odds Ratio (95% CI) |
|---|---|---|---|---|
|
Intercepción |
-1.443 |
1.602 |
0.2056 |
– |
|
Raza negra |
-0,082 |
0,015 |
0.9039 |
0,921 (0,244, 3,483) |
|
Raza hispana |
-1,564 |
9.497 |
0,0021 |
0,209 (0,077, 0,566) |
|
Otra raza |
0.548 |
1,124 |
0,2890 |
1,730 (0,628,4,767) |
|
Edad de la madre (años.) |
00,037 |
1,198 |
0,2737 |
0,963 (0,901, 1,030) |
Respecto al parto prematuro, la única diferencia estadísticamente significativa es entre las madres hispanas y las blancas (p=0,0021). Las madres hispanas tienen un 80% menos de probabilidades de desarrollar un parto prematuro que las madres blancas (odds ratio = 0,209), ajustado por la edad de la madre.
Los métodos multivariables son complejos desde el punto de vista computacional y generalmente requieren el uso de un paquete informático estadístico. Los métodos multivariables pueden utilizarse para evaluar y ajustar los factores de confusión, para determinar si existe una modificación del efecto o para evaluar las relaciones de varios factores de exposición o de riesgo sobre un resultado simultáneamente. Los análisis multivariables son complejos y siempre deben planificarse para reflejar relaciones biológicamente plausibles. Aunque es relativamente fácil considerar una variable adicional en un modelo de regresión lineal múltiple o logística múltiple, sólo deben incluirse las variables que sean clínicamente significativas.
Es importante recordar que los modelos multivariables sólo pueden ajustar o dar cuenta de las diferencias en las variables de confusión que se midieron en el estudio. Además, los modelos multivariables sólo deben utilizarse para tener en cuenta los factores de confusión cuando hay algún solapamiento en la distribución del factor de confusión en cada uno de los grupos de factores de riesgo.
Los análisis estratificados son muy informativos, pero si las muestras en estratos específicos son demasiado pequeñas, los análisis pueden carecer de precisión. Al planificar los estudios, los investigadores deben prestar mucha atención a los posibles modificadores del efecto. Si se sospecha que una asociación entre una exposición o un factor de riesgo es diferente en grupos específicos, el estudio debe diseñarse para garantizar un número suficiente de participantes en cada uno de esos grupos. Deben utilizarse fórmulas de tamaño de la muestra para determinar el número de sujetos necesarios en cada estrato para garantizar una precisión o potencia adecuada en el análisis.
Volver al principio | página anterior | página siguiente