Výsledek v logistické regresní analýze je často kódován jako 0 nebo 1, kde 1 znamená, že výsledek zájmu je přítomen, a 0 znamená, že výsledek zájmu chybí. Pokud definujeme p jako pravděpodobnost, že výsledek je 1, lze model vícenásobné logistické regrese zapsat takto:
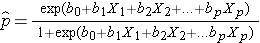
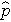je očekávaná pravděpodobnost, že výsledek je přítomen; X1 až Xp jsou různé nezávislé proměnné a b0 až bp jsou regresní koeficienty. Model vícenásobné logistické regrese se někdy zapisuje jinak. V následujícím tvaru je výsledek očekávaným logaritmem pravděpodobnosti, že výsledek je přítomen,
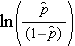
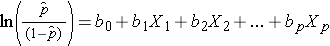
Všimněte si, že pravá strana výše uvedené rovnice vypadá jako rovnice vícenásobné lineární regrese. Technika odhadu regresních koeficientů v logistickém regresním modelu se však liší od techniky odhadu regresních koeficientů v modelu vícenásobné lineární regrese. V logistické regresi koeficienty odvozené z modelu (např. b1) udávají změnu očekávané logaritmické šance vzhledem k jednotkové změně X1 při zachování všech ostatních prediktorů konstantních. Proto antilog odhadnutého regresního koeficientu, exp(bi), vytváří poměr šancí, jak je znázorněno v příkladu níže.
Příklad logistické regrese – souvislost mezi obezitou a KVO
Předtím jsme analyzovali údaje ze studie určené k posouzení souvislosti mezi obezitou (definovanou jako BMI > 30) a incidencí kardiovaskulárního onemocnění. Údaje byly shromážděny od účastníků, kteří byli ve věku 35 až 65 let a na počátku studie netrpěli kardiovaskulárním onemocněním (KVO). Každý účastník byl sledován po dobu 10 let z hlediska rozvoje kardiovaskulárního onemocnění. Souhrn údajů naleznete na straně 2 tohoto modulu. Neupravené neboli hrubé relativní riziko bylo RR = 1,78 a neupravený neboli hrubý poměr šancí byl OR = 1,93. Rovněž jsme určili, že věk je matoucím faktorem, a pomocí Cochran-Mantel-Haenszelovy metody jsme odhadli upravené relativní riziko RRCMH =1,44 a upravený poměr šancí ORCMH =1,52. Ukázalo se, že věk je matoucím faktorem. Nyní použijeme logistickou regresní analýzu k posouzení souvislosti mezi obezitou a výskytem kardiovaskulárních onemocnění s úpravou na věk.
Z logistické regresní analýzy vyplývá následující:
|
Nezávislá proměnná |
Regresní koeficient |
Chi-kvadrát |
P-hodnota |
|---|---|---|---|
|
Intercept |
-2.367 |
307.38 |
0.0001 |
|
Obezita |
0,658 |
9,87 |
0.0017 |
Prostý logistický regresní model vztahuje obezitu k logaritmické šanci na výskyt KVO:
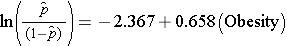
Obezita je v modelu indikátorovou proměnnou, kódovanou následovně: 1=obézní a 0=není obézní. Logaritmická šance na výskyt CVD je 0,658krát vyšší u obézních osob ve srovnání s neobézními. Pokud vezmeme antilog regresního koeficientu, exp(0,658) = 1,93, dostaneme hrubý nebo neupravený poměr šancí. Šance na vznik KVO je u obézních osob 1,93krát vyšší než u neobézních osob. Vztah mezi obezitou a výskytem KVO je statisticky významný (p=0,0017). Všimněte si, že testovací statistiky pro posouzení významnosti regresních parametrů v logistické regresní analýze jsou založeny na statistice chí-kvadrát, na rozdíl od statistiky t, jak tomu bylo v případě lineární regresní analýzy. Je to proto, že k odhadu regresních parametrů se používá jiná technika odhadu, která se nazývá odhad maximální věrohodnosti (technické podrobnosti viz Hosmer a Lemeshow3).
Mnoho statistických výpočetních balíků také v rámci postupu logistické regresní analýzy generuje poměry šancí a také 95% intervaly spolehlivosti pro poměry šancí. V tomto příkladu je odhad poměru šancí 1,93 a 95% interval spolehlivosti je (1,281, 2,913).
Při zkoumání souvislosti mezi obezitou a KVO jsme dříve určili, že věk je matoucím faktorem. následující model vícenásobné logistické regrese odhaduje souvislost mezi obezitou a výskytem KVO s úpravou na věk. V modelu opět uvažujeme dvě věkové skupiny (méně než 50 let a 50 let a více). Pro účely analýzy je věková skupina kódována následovně: 1=50 let a více a 0=méně než 50 let.
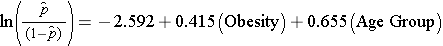
Pokud vezmeme antilog regresního koeficientu spojeného s obezitou, exp(0,415) = 1,52, dostaneme poměr šancí upravený podle věku. Šance na vznik KVO je u obézních osob 1,52krát vyšší ve srovnání s neobézními osobami, po úpravě na věk. V části 9.2 jsme použili Cochranovu-Mantelovu-Haenszelovu metodu k vytvoření poměru šancí upraveného podle věku a zjistili jsme následující:
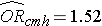
To ilustruje, jak lze použít vícenásobnou logistickou regresní analýzu k zohlednění zmatků. Modely lze rozšířit tak, aby zohledňovaly několik matoucích proměnných současně. Vícenásobnou logistickou regresní analýzu lze také použít k posouzení zmatení a modifikace účinku a přístupy jsou totožné s těmi, které se používají při vícenásobné lineární regresní analýze. Vícenásobnou logistickou regresní analýzu lze také použít ke zkoumání vlivu více rizikových faktorů (na rozdíl od zaměření se na jediný rizikový faktor) na dichotomický výsledek.
Příklad – Rizikové faktory spojené s nízkou porodní hmotností dítěte
Předpokládejme, že se zkoušející zabývají také nepříznivými výsledky těhotenství, včetně těhotenského diabetu, preeklampsie (tj. hypertenze vyvolané těhotenstvím) a předčasného porodu. Připomeňme, že studie se zúčastnilo 832 těhotných žen, které poskytly demografické a klinické údaje. Ve studovaném vzorku se u 22 (2,7 %) žen vyvinula preeklampsie, u 35 (4,2 %) gestační diabetes a u 40 (4,8 %) předčasný porod. Předpokládejme, že chceme posoudit, zda existují rozdíly v každém z těchto nepříznivých výsledků těhotenství podle rasy/etnické příslušnosti, upravené podle věku matky. Byly provedeny tři samostatné logistické regresní analýzy vztahující každý výsledek, posuzovaný samostatně, ke 3 dummy nebo indikátorovým proměnným odrážejícím rasu matky a věk matky v letech. Výsledky jsou uvedeny níže.
|
Výsledek: Preeklampsie |
Regresní koeficient |
Chi-kvadrát |
P-hodnota |
Odds Ratio (95% CI) |
|---|---|---|---|---|
|
Intercept |
-3.066 |
4.518 |
0.0335 |
– |
|
Černá rasa |
2,191 |
12,640 |
0,0004 |
8.948 (2,673, 29,949) |
|
Hispánská rasa |
-0,1053 |
0,0325 |
0,8570 |
0.900 (0,286, 2,829) |
|
Jiná rasa |
0,0586 |
0,0021 |
0.9046 |
1,060 (0,104, 3,698) |
|
Věk matky (let) |
-0,0252 |
0.3574 |
0,5500 |
0,975 (0,898, 1,059) |
Jediný statisticky významný rozdíl v preeklampsii je mezi černošskými a bílými matkami.
Černošské matky mají téměř 9krát vyšší pravděpodobnost vzniku preeklampsie než bílé matky, upraveno podle věku matky. Interval spolehlivosti 95 % pro poměr šancí srovnávající černošky a bělošky, u kterých se preeklampsie vyvine, je velmi široký (2,673 až 29,949). To je způsobeno tím, že ve studii je malý počet výsledných událostí (v celkovém vzorku se preeklampsie vyvinula pouze u 22 žen) a malý počet žen černé rasy. Tuto souvislost je tedy třeba interpretovat s opatrností.
Přestože je poměr šancí statisticky významný, interval spolehlivosti naznačuje, že velikost účinku může být od 2,6násobného zvýšení až po 29,9násobné zvýšení. K přesnějšímu odhadu účinku je zapotřebí rozsáhlejší studie.
|
Gestační diabetes |
Regresní koeficient |
Chi-square |
P-value |
Odds Ratio (95% CI) |
|---|---|---|---|---|
|
Intercept |
-5.823 |
22,968 |
0,0001 |
– |
|
Černá rasa |
1,621 |
6.660 |
0,0099 |
5,056 (1,477, 17,312) |
|
Hispánská rasa |
0,581 |
1.766 |
0,1839 |
1,787 (0,759, 4,207) |
|
Jiná rasa |
1,348 |
5.917 |
0,0150 |
3,848 (1,299, 11,395) |
|
Věk matky (let) |
0,071 |
4.314 |
0,0378 |
1,073 (1,004, 1,147) |
Pokud jde o těhotenský diabetes, existují statisticky významné rozdíly mezi černošskými a bílými matkami (p=0,0099) a mezi matkami, které se identifikují jako jiná rasa ve srovnání s běloškami (p=0,0150), upraveno podle věku matky. Věk matky je také statisticky významný (p=0,0378), u starších žen je vyšší pravděpodobnost vzniku těhotenské cukrovky, upraveno podle rasy/etnicity.
|
Výsledky: Předčasný porod |
Regresní koeficient |
Chi-kvadrát |
P-hodnota |
Odds Ratio (95% CI) |
|---|---|---|---|---|
|
Intercept |
-1.443 |
1.602 |
0.2056 |
– |
|
Černá rasa |
-0,082 |
0,015 |
0.9039 |
0,921 (0,244, 3,483) |
|
Hispánská rasa |
-1,564 |
9.497 |
0,0021 |
0,209 (0,077, 0,566) |
|
Jiná rasa |
0.548 |
1,124 |
0,2890 |
1,730 (0,628,4,767) |
|
Věk matky (v letech.) |
00,037 |
1,198 |
0,2737 |
0,963 (0,901, 1,030) |
Co se týče porodu před termínem, jediný statisticky významný rozdíl je mezi hispánskými a bílými matkami (p=0,0021). U hispánských matek je o 80 % nižší pravděpodobnost vzniku porodu před termínem než u bílých matek (poměr šancí = 0,209), upravený podle věku matky.
Multivariační metody jsou výpočetně složité a obvykle vyžadují použití statistického výpočetního balíku. Vícerozměrné metody lze použít k posouzení a úpravě zmatení, k určení, zda dochází k modifikaci účinku, nebo k posouzení vztahů několika expozičních nebo rizikových faktorů na výsledek současně. Vícerozměrné analýzy jsou složité a měly by být vždy plánovány tak, aby odrážely biologicky věrohodné vztahy. I když je relativně snadné zvážit další proměnnou ve vícenásobném lineárním nebo vícenásobném logistickém regresním modelu, měly by být zahrnuty pouze proměnné, které jsou klinicky významné.
Je důležité si uvědomit, že vícerozměrné modely mohou upravit nebo zohlednit pouze rozdíly v matoucích proměnných, které byly ve studii měřeny. Kromě toho by se multivariační modely měly používat k zohlednění matoucích proměnných pouze tehdy, pokud se distribuce matoucích proměnných v jednotlivých skupinách rizikových faktorů překrývá.
Stratifikované analýzy jsou velmi informativní, ale pokud jsou vzorky v určitých vrstvách příliš malé, mohou analýzy postrádat přesnost. Při plánování studií musí zkoušející věnovat pečlivou pozornost potenciálním modifikátorům účinku. Pokud existuje podezření, že souvislost mezi expozicí nebo rizikovým faktorem je ve specifických skupinách odlišná, musí být studie navržena tak, aby byl zajištěn dostatečný počet účastníků v každé z těchto skupin. Ke stanovení počtu subjektů potřebných v každé vrstvě, aby byla zajištěna dostatečná přesnost nebo síla analýzy, musí být použity vzorce pro velikost vzorku.
zpět na začátek | předchozí strana | další strana