Zjednodušený popis
Uvažujme nejprve o vazbě pí v ethenu z hlediska zjednodušené teorie MO (v tomto příkladu nebudeme brát v úvahu vazby sigma v molekule a budeme uvažovat pouze o vazbě π). Začneme se dvěma atomovými orbitaly: jedním nehybridizovaným 2p orbitalem od každého uhlíku. Každý z nich obsahuje jeden elektron. V teorii MO se tyto dva atomové matematicky spojí a vytvoří dva molekulové orbitaly pí, jeden nízkoenergetický vazebný orbital pí a jeden vysokoenergetický antivazebný orbital pí*.

Molekulární orbitaly pro ethen (ethylen)
Ve vazebném orbitalu pí spolu oba zastíněné laloky orbitalů p konstruktivně interagují, stejně jako dva nezastíněné laloky (nezapomeňte, že libovolná volba zastínění představuje matematická znaménka (+) a (-) pro matematickou vlnovou funkci popisující orbital). Mezi oběma jádry uhlíku v molekulovém orbitalu je zvýšená elektronová hustota – jedná se o vazebnou interakci.
V antivazebném orbitalu pi* s vyšší energií interaguje zastíněný lalok jednoho orbitalu p destruktivně s nezastíněným lalokem druhého orbitalu p, což vede k uzlu mezi oběma jádry a celkovému odpuzování mezi jádry uhlíku.
Znovu použijeme princip „budování“ a umístíme dva elektrony do vazebného molekulového orbitalu pi s nižší energií. Antivazebný orbital pi* zůstává prázdný.
Podrobnější MO popis ethenu
Teorie molekulových orbitalů byla velmi úspěšně aplikována na velké konjugované systémy, zejména ty, které obsahují řetězce atomů uhlíku se střídajícími se jednoduchými a dvojnými vazbami. Aproximace zavedená Hückelem v roce 1931 uvažuje pouze delokalizované p elektrony pohybující se v rámci \pi -vazby. Jedná se vlastně o sofistikovanější verzi modelu volných elektronů. Pro úvodní kurz organické chemie nemusíme použít celou Hückelovu matematiku, ale pro ty, kteří chtějí proniknout hlouběji, je zde uvedena podrobnější analýza.
Nejjednodušším uvažovaným uhlovodíkem, který vykazuje vazbu \pi, je ethen (ethylen), který se skládá ze čtyř atomů vodíku a dvou atomů uhlíku. Experimentálně víme, že úhly H-C-H a H-C-C v ethenu jsou přibližně 120°. Tento úhel naznačuje, že atomy uhlíku jsou sp2 hybridizované, což znamená, že singulárně obsazený orbital sp2 na jednom uhlíku se překrývá s singulárně obsazeným orbitalem s na každém H a singulárně obsazeným lalokem sp2 na druhém C. Každý uhlík tak tvoří sadu tří \sigma vazeb: dvě C-H (sp2 + s) a jednu C-C (sp2 + sp2) (část a) obrázku 13.1. níže).

Obrázek 13.1. (a) Vazbový rámec σ je tvořen překrytím dvou sad singulárně obsazených hybridních orbitalů uhlíku sp2 a čtyř singulárně obsazených orbitalů vodíku 1s za vzniku vazeb elektronových párů. Tím se využívá 10 z 12 valenčních elektronů k vytvoření celkem pěti σ vazeb (čtyři vazby C-H a jedna vazba C-C). (b) Na každém atomu uhlíku zůstává jeden singulárně obsazený nehybridizovaný orbital 2pz, který tvoří vazbu π uhlík-uhlík. (Poznámka: podle konvence je u planárních molekul osa kolmá na molekulovou rovinu osou z.)
Hückelova aproximace se používá k určení energií a tvarů \pi molekulových orbitalů v konjugovaných systémech. V rámci Hückelovy aproximace lze kovalentní vazby v těchto uhlovodících rozdělit do dvou nezávislých „rámců“: \sigma – vazebný rámec a \sigma – vazebný rámec. Vlnové funkce použité k popisu vazebných orbitalů v každém rámci vyplývají z různých kombinací atomových orbitalů. Metoda se omezuje na řešení konjugovaných uhlovodíků a konkrétně jsou zahrnuty pouze \pi elektronové molekulové orbitaly, protože ty určují obecné vlastnosti těchto molekul; sigma elektrony jsou ignorovány. Tento postup se označuje jako sigma-pi separabilita a je odůvodněn ortogonalitou \sigma a \pi orbitalů v planárních molekulách. Z tohoto důvodu je Hückelova metoda omezena na planární systémy. Hückelova aproximace předpokládá, že elektrony ve vazbách \pi „cítí“ elektrostatický potenciál způsobený celým vazebným rámcem \sigma v molekule (tj. zaměřuje se pouze na tvorbu vazeb \pi za předpokladu, že vazební rámec \sigma již byl vytvořen).
Konjugované systémy
Konjugovaný systém má oblast překrývajících se p-orbitálů, přemosťujících mezilehlé jednoduché vazby, které umožňují delokalizaci \pi elektronů přes všechny sousední zarovnané p-orbitály. Tyto elektrony \pi nepatří jediné vazbě nebo jedinému atomu, ale spíše skupině atomů.
Eten
Předtím, než se budeme zabývat Hückelovým zpracováním ethenu, je prospěšné zopakovat si obecný vazebný obraz molekuly. Vazba v ethenu zahrnuje sp^2 hybridizaci atomových orbitalů 2s , 2p_x a 2p_y na každém atomu uhlíku; orbitaly 2p_z zůstávají nedotčeny (obrázek 13.2).
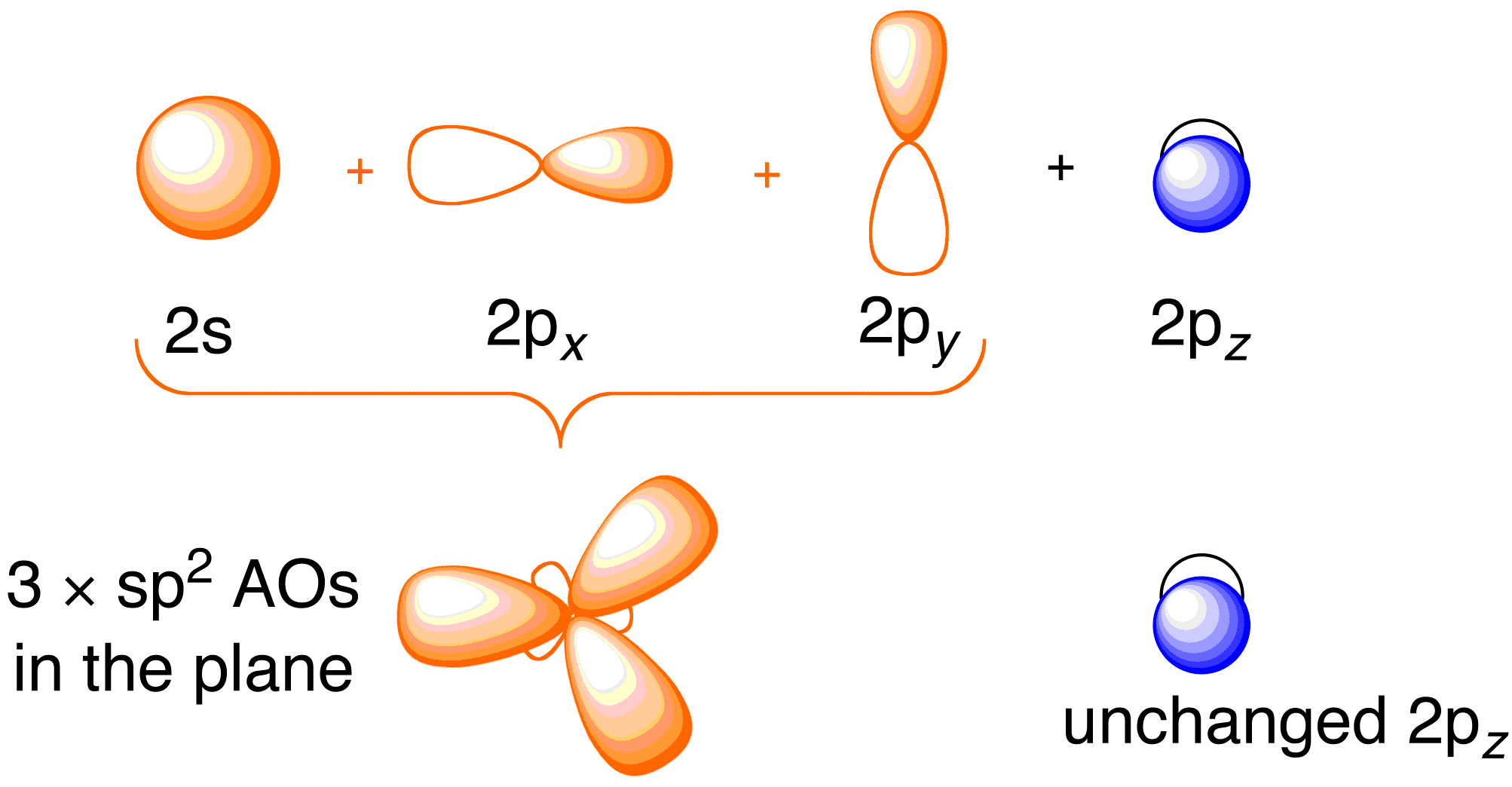
Obrázek 13.2. Hybridizace atomových orbitalů uhlíku za účelem získání hybridních orbitalů sp^2 pro vazbu s atomy vodíku v ethenu. Obrázek použit se svolením z ChemTube (CC-SA-BY-NC; Nick Greeves).
Použití hybridních orbitalů v zde popsaném přístupu k molekulovým orbitálům je pouze pohodlné a neodvolává se (přímo) na teorii valenční vazby. Identický popis lze získat použitím výhradně atomových orbitalů na uhlíku, ale interpretace výsledných vlnových funkcí je méně intuitivní. Například i-tý molekulový orbital lze popsat pomocí hybridních orbitalů
\
nebo pomocí atomových orbitalů.
\
kde \{a_i\} a \{c_i\} jsou koeficienty rozšíření. Obojí popis bude fungovat a oba přístupy jsou totožné, protože
\
kde \{c_i\} jsou koeficienty popisující hybridizovaný orbital.
Vazba vzniká smícháním elektronů v hybridních orbitalech sp^2 na uhlíku a elektronů v atomových orbitalech 1s čtyř atomů vodíku (obrázek 13.2. vlevo nahoře), což vede ke vzniku \sigma – vazebného rámce. Vazbový rámec \pi je výsledkem nehybridizovaných orbitalů 2p_z (obrázek 13.2. vpravo nahoře). Nezávislost těchto dvou rámců je demonstrována na výsledném diagramu molekulových orbitalů na obrázku níže; Hückelova teorie se zabývá pouze popisem molekulových orbitalů a energií \pi vazebného rámce.

Obrázek 13.3: Molekulové orbitaly prokazující sigma-pi separabilitu \pi vazebného rámce (modře) a \sigma vazebného rámce (červeně) ethylenu.
Hückelovo zpracování se zabývá pouze popisem molekulových orbitalů a energií \pi vazebného rámce.
Protože Hückelova teorie je speciální úvahou teorie molekulových orbitalů, lze molekulové orbitaly | \psi_i \kruhu popsat jako lineární kombinaci 2p_z atomových orbitalů \phi u uhlíku s jejich odpovídajícími koeficienty \{c_i\}:
\
Kompletní analýzu kvantové chemie pomocí Schrödingerovy rovnice (není nutná pro výuku organické chemie) naleznete na této stránce Libretexts.
Tyto molekulové orbitaly tvoří π-vazbový rámec, a protože každý uhlík přispívá do tohoto rámce jedním elektronem, je v základním stavu obsazen pouze nejnižší molekulový orbital ( | \psi_1 \rangle ) (obrázek ). Odpovídající elektronová konfigurace je pak \pi_1^2 .

Obrázek 13.4: Schematické znázornění rámce molekulových orbitalů \pi pro ethylen . Všimněte si, že antivazebný molekulový orbital má podle očekávání o jeden uzel více než vazebný molekulový orbital, protože má vyšší energii.
HOMO a LUMO jsou zkratky pro nejvýše obsazený molekulový orbital a nejnižší neobsazený molekulový orbital a často se označují jako hraniční orbitaly. Energetický rozdíl mezi HOMO a LUMO se označuje jako mezera HOMO-LUMO.
Vypočtené 3-D molekulové orbitaly \pi jsou znázorněny na obrázku 13.5.

Obrázek 13.5: Vypočtené molekulové orbitaly \pi pro ethylen . (Vlevo) vazebný orbital (ψ1) a (vpravo) antivazebný orbital (ψ2).
Přispěvatelé
- Seymour Blinder (emeritní profesor chemie a fyziky na Michiganské univerzitě v Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
.
