V normálním rozdělení jsou data rozložena symetricky bez zkreslení. Při vynesení do grafu mají data zvonovitý tvar, přičemž většina hodnot se shlukuje kolem centrální oblasti a s rostoucí vzdáleností od středu se zužuje.
Normální rozdělení se kvůli svému tvaru nazývá také Gaussovo rozdělení nebo zvonovitá křivka.

- Proč jsou normální rozdělení důležitá?
- Jaké jsou vlastnosti normálních rozdělení?
- Jaké je vaše skóre plagiátorství
- Empirické pravidlo
- Centrální limitní věta
- Formule normální křivky
- Co je to standardní normální rozdělení?
- Zjištění pravděpodobnosti pomocí z-rozdělení
- Často kladené otázky o normálním rozdělení
Proč jsou normální rozdělení důležitá?
Všechny druhy proměnných v přírodních a společenských vědách jsou normálně nebo přibližně normálně rozděleny. Výška, porodní hmotnost, schopnost číst, spokojenost s prací nebo skóre v testu SAT jsou jen některé příklady takových proměnných.
Protože jsou normálně rozložené proměnné tak běžné, mnoho statistických testů je navrženo pro normálně rozložené populace.
Poznání vlastností normálních rozdělení znamená, že můžete používat inferenční statistiku k porovnávání různých skupin a k odhadům o populacích pomocí vzorků.
Jaké jsou vlastnosti normálních rozdělení?
Normální rozdělení má klíčové vlastnosti, které lze snadno rozpoznat v grafech:
- Průměr, medián a modus jsou přesně stejné.
- Rozdělení je symetrické kolem průměru – polovina hodnot spadá pod průměr a polovina nad průměr.
- Rozdělení lze popsat dvěma hodnotami: průměrem a směrodatnou odchylkou.


Střední hodnota je parametr umístění, zatímco směrodatná odchylka je parametr měřítka.
Střední hodnota určuje, kde je vrchol křivky vystředěn. Zvyšování střední hodnoty posouvá křivku doprava, zatímco její snižování doleva.


Standardní odchylka křivku roztahuje nebo stlačuje. Malá směrodatná odchylka vede k úzké křivce, zatímco velká směrodatná odchylka vede k široké křivce.


Empirické pravidlo
Empirické pravidlo, nebo 68-95-99.7 pravidlo, říká, kde leží většina hodnot v normálním rozdělení:
- Přibližně 68 % hodnot se nachází do 1 směrodatné odchylky od průměru.
- Přibližně 95 % hodnot se nachází do 2 směrodatných odchylek od průměru.
- Přibližně 99,7 % hodnot se nachází do 3 směrodatných odchylek od průměru.
Podle empirického pravidla:
- Přibližně 68 % skóre je mezi 1000 a 1300, 1 směrodatná odchylka nad a pod průměrem.
- Přibližně 95 % výsledků je mezi 850 a 1450, 2 směrodatné odchylky nad a pod průměrem.
- Přibližně 99,7 % výsledků je mezi 700 a 1600, 3 směrodatné odchylky nad a pod průměrem.


Empirické pravidlo je rychlý způsob, jak získat přehled o datech a zkontrolovat, zda nejsou odlehlé nebo extrémní hodnoty, které se neřídí tímto vzorem.
Pokud se data z malých vzorků přesně neřídí tímto vzorem, mohou být vhodnější jiná rozdělení, například t-rozdělení. Jakmile určíte rozdělení vaší proměnné, můžete použít vhodné statistické testy.
Centrální limitní věta
Centrální limitní věta je základem toho, jak ve statistice fungují normální rozdělení.
Abyste ve výzkumu získali dobrou představu o průměru populace, měli byste v ideálním případě shromáždit data z více náhodných vzorků v rámci populace. Výběrové rozdělení střední hodnoty je rozdělení středních hodnot těchto různých vzorků.
Centrální limitní věta ukazuje následující:
- Zákon velkých čísel: S rostoucí velikostí vzorku (neboli počtem vzorků) se pak výběrový průměr bude blížit průměru populace.
- Při více velkých vzorcích je výběrové rozdělení průměru normálně rozděleno, i když vaše původní proměnná není normálně rozdělena.
Parametrické statistické testy obvykle předpokládají, že vzorky pocházejí z normálně rozdělených populací, ale centrální limitní věta znamená, že tento předpoklad není nutné splnit, pokud máte dostatečně velký vzorek.
Parametrické testy můžete použít pro velké vzorky z populací s jakýmkoli typem rozdělení, pokud jsou splněny další důležité předpoklady. Za velký vzorek se obecně považuje vzorek o velikosti 30 nebo více.
U malých vzorků je předpoklad normality důležitý, protože není známo výběrové rozdělení střední hodnoty. Pro přesné výsledky si musíte být jisti, že populace je normálně rozdělena, než budete moci použít parametrické testy s malými vzorky.
Formule normální křivky
Jakmile máte střední hodnotu a směrodatnou odchylku normálního rozdělení, můžete na data dosadit normální křivku pomocí funkce hustoty pravděpodobnosti.


Ve funkci hustoty pravděpodobnosti vám plocha pod křivkou udává pravděpodobnost. Normální rozdělení je rozdělením pravděpodobnosti, takže celková plocha pod křivkou je vždy 1 neboli 100 %.
Vzorec pro normální funkci hustoty pravděpodobnosti vypadá poměrně složitě. K jeho použití však stačí znát populační průměr a směrodatnou odchylku.
Pro libovolnou hodnotu x můžete do vzorce dosadit průměr a směrodatnou odchylku a zjistit hustotu pravděpodobnosti proměnné, která nabývá dané hodnoty x.
| Normální vzorec hustoty pravděpodobnosti | Vysvětlení |
|---|---|
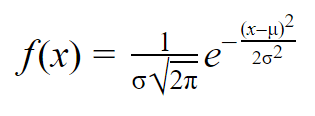 |
|
Na grafu funkce hustoty pravděpodobnosti je pravděpodobnost zastíněná oblast pod křivkou, která leží napravo od místa, kde se skóre SAT rovná 1380.


Můžete najít hodnotu pravděpodobnosti tohoto skóre pomocí standardního normálního rozdělení.
Co je to standardní normální rozdělení?
Standardní normální rozdělení, nazývané také z-rozdělení, je speciální normální rozdělení, kde střední hodnota je 0 a směrodatná odchylka je 1.
Každé normální rozdělení je verzí standardního normálního rozdělení, které bylo roztaženo nebo stlačeno a posunuto vodorovně doprava nebo doleva.


Když se jednotlivá pozorování z normálního rozdělení označují jako x, v z-rozdělení se označují jako z. Každé normální rozdělení lze převést na standardní normální rozdělení tak, že jednotlivé hodnoty převedeme na z-skóre.
Z-skóre říká, kolik směrodatných odchylek od průměru leží každá hodnota.


Pro zjištění z-skóre hodnoty stačí znát průměr a směrodatnou odchylku rozdělení.
| Vzorec pro Z-skóre | Vysvětlení |
|---|---|
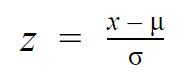 |
|
Normální rozdělení převádíme na standardní normální rozdělení z několika důvodů:
- Chceme-li zjistit pravděpodobnost, že pozorování v rozdělení spadají nad nebo pod danou hodnotu.
- K nalezení pravděpodobnosti, že se výběrový průměr významně liší od známého populačního průměru.
- K porovnání výsledků na různých rozděleních s různými průměry a směrodatnými odchylkami.
Zjištění pravděpodobnosti pomocí z-rozdělení
Každému z-rozdělení je přiřazena pravděpodobnost neboli p-hodnota, která udává pravděpodobnost výskytu hodnot pod daným z-rozdělením. Pokud převedete jednotlivou hodnotu na z-skóre, můžete pak v normálním rozdělení zjistit pravděpodobnost výskytu všech hodnot do této hodnoty.
Střední hodnota našeho rozdělení je 1150 a směrodatná odchylka 150. Z-skóre vám řekne, o kolik směrodatných odchylek je hodnota 1380 vzdálena od průměru.
| Formule | Výpočet |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1. Jaký je výsledek?53 |
Pro z-skóre 1,53 je p-hodnota 0,937. V případě, že je z-skóre 1,53, je p-hodnota 0,937. To je pravděpodobnost, že skóre testu SAT je 1380 nebo méně (93,7 %), a je to plocha pod křivkou vlevo od stínované oblasti.


Pro zjištění stínované oblasti odečtete 0. To je pravděpodobnost, že skóre testu SAT je 1380 nebo méně.937 od 1, což je celková plocha pod křivkou.
Pravděpodobnost x>1380 = 1 – 0,937 = 0,063
To znamená, že je pravděpodobné, že pouze 6,3 % výsledků SAT ve vašem vzorku přesahuje 1380.
Často kladené otázky o normálním rozdělení
V normálním rozdělení jsou data symetricky rozdělena bez zkreslení. Většina hodnot se shlukuje kolem centrální oblasti, přičemž se vzdáleností od středu se hodnoty zužují.
Míry centrální tendence (průměr, modus a medián) jsou v normálním rozdělení naprosto stejné.
Standardní normální rozdělení, nazývané také z-rozdělení, je speciální normální rozdělení, kde průměr je 0 a směrodatná odchylka je 1.
Každé normální rozdělení lze převést na standardní normální rozdělení tak, že jednotlivé hodnoty převedeme na z-rozdělení. V z-rozdělení z-skóre říká, kolik směrodatných odchylek od průměru leží každá hodnota.
Empirické pravidlo neboli pravidlo 68-95-99,7 říká, kde leží většina hodnot v normálním rozdělení:
- Přibližně 68 % hodnot leží do 1 směrodatné odchylky od průměru.
- Přibližně 95 % hodnot leží do 2 směrodatných odchylek od průměru.
- Přibližně 99,7 % hodnot je v rozmezí 3 směrodatných odchylek od průměru.
Empirické pravidlo je rychlý způsob, jak získat přehled o datech a zkontrolovat případné odlehlé nebo extrémní hodnoty, které se neřídí tímto vzorcem.
T-distribuce je způsob popisu souboru pozorování, kde většina pozorování spadá blízko průměru a zbytek pozorování tvoří chvosty na obou stranách. Je to typ normálního rozdělení, který se používá pro menší výběry, kde není znám rozptyl v datech.
Při vynesení do grafu tvoří t-rozdělení zvonovou křivku. Matematicky ho lze popsat pomocí střední hodnoty a směrodatné odchylky.
.

