Trojúhelník s jedním pravým úhlem se nazývá pravoúhlý trojúhelník. Strana protilehlá pravému úhlu se nazývá přepona trojúhelníku. Zbývající dvě strany se nazývají nohy. Ostatní dva úhly nemají žádný zvláštní název, ale jsou vždy komplementární. Chápete proč? Celkový součet úhlů trojúhelníku je 180 stupňů a pravý úhel má 90 stupňů, takže součet ostatních dvou musí být 90 stupňů.
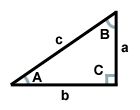
Výše uvedený trojúhelník má stranu c jako přeponu, strany a a b jako odvěsny a úhel C jako pravý úhel. Úhly A aB jsou komplementární.
Existují dva typy pravoúhlých trojúhelníků, které by měl každý matematik dobře znát. Jedním z nich je pravoúhlý trojúhelník, který vznikne, když z vrcholu rovnostranného trojúhelníku vyneseme výšku a vytvoříme dva shodné pravoúhlé trojúhelníky. Úhly tohoto trojúhelníku budou 30, 60 a 90 stupňů, což dalo trojúhelníku jeho název: trojúhelník 30-60-90. Poměr délek stran v takových trojúhelnících je vždy stejný: má-li rameno naproti úhlu 30 stupňů délku x, bude mít rameno naproti úhlu 60 stupňů délku x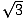
a přepona napříč od pravého úhlu bude mít délku 2x. Zde je zobrazen trojúhelník 30-60-90.
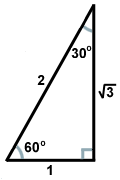
Druhý běžný pravoúhlý trojúhelník vznikne tak, že dvojice trojúhelníků vznikne, když úhlopříčka rozdělí čtverec na dva trojúhelníky. Každý z těchto trojúhelníků je shodný a má úhly o rozměrech 45, 45 a 90 stupňů. Jestliže rameny protilehlých úhlů 45 stupňů mají délku x, přepona má délku x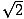
. Tento poměr platí pro všechny trojúhelníky 45-45-90. Trojúhelníky 45-45-90 se také často nazývají rovnoramenné pravoúhlé trojúhelníky.
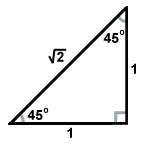
Jednou z posledních vlastností, kterou je třeba si uvědomit, je, že odvěsny pravoúhlého trojúhelníku jsou zároveň jeho výškami. Plocha pravoúhlého trojúhelníku je tedy polovinou součinu délek jeho ramen.