I en normalfordeling er data symmetrisk fordelt uden skævhed. Når dataene plottes på en graf, følger de en klokkeform, hvor de fleste værdier samler sig omkring et centralt område og aftager, efterhånden som de bevæger sig længere væk fra centrum.
Normalfordelinger kaldes også for Gauss-fordelinger eller klokkekurver på grund af deres form.

Hvorfor er normalfordelinger vigtige?
Alle former for variabler inden for natur- og samfundsvidenskab er normalt eller tilnærmelsesvis normalfordelte. Højde, fødselsvægt, læsefærdigheder, jobtilfredshed eller SAT-scoringer er blot nogle få eksempler på sådanne variabler.
Da normalfordelte variabler er så almindelige, er mange statistiske test designet til normalfordelte populationer.
Ved at forstå egenskaberne ved normalfordelinger kan du bruge inferensstatistik til at sammenligne forskellige grupper og foretage skøn over populationer ved hjælp af stikprøver.
Hvad er egenskaberne ved normalfordelinger?
Normalfordelinger har vigtige egenskaber, som er nemme at få øje på i grafer:
- Middelværdien, medianen og modus er nøjagtig de samme.
- Fordelingen er symmetrisk omkring middelværdien – halvdelen af værdierne falder under middelværdien og halvdelen over middelværdien.
- Fordelingen kan beskrives ved hjælp af to værdier: middelværdien og standardafvigelsen.


Middelværdien er beliggenhedsparameteren, mens standardafvigelsen er skalaparameteren.
Middelværdien bestemmer, hvor kurvens top er centreret. En forøgelse af middelværdien flytter kurven til højre, mens en forringelse flytter kurven til venstre.


Standardafvigelsen strækker eller klemmer kurven. En lille standardafvigelse resulterer i en smal kurve, mens en stor standardafvigelse fører til en bred kurve.


Empirisk regel
Den empiriske regel, eller 68-95-99.7-reglen, fortæller dig, hvor de fleste af dine værdier ligger i en normalfordeling:
- Omkring 68% af værdierne ligger inden for 1 standardafvigelse fra middelværdien.
- Omkring 95% af værdierne ligger inden for 2 standardafvigelser fra middelværdien.
- Omkring 99,7% af værdierne ligger inden for 3 standardafvigelser fra middelværdien.
Ved anvendelse af den empiriske regel:
- Omkring 68% af scoren ligger mellem 1000 og 1300, 1 standardafvigelse over og under gennemsnittet.
- Omkring 95 % af scorerne ligger mellem 850 og 1450, 2 standardafvigelser over og under middelværdien.
- Omkring 99,7 % af scorerne ligger mellem 700 og 1600, 3 standardafvigelser over og under middelværdien.


Den empiriske regel er en hurtig måde at få et overblik over dine data på og kontrollere for eventuelle outliers eller ekstreme værdier, der ikke følger dette mønster.
Hvis data fra små stikprøver ikke følger dette mønster nøje, kan andre fordelinger som t-fordelingen være mere hensigtsmæssige. Når du har identificeret fordelingen af din variabel, kan du anvende passende statistiske test.
Central grænsesætning
Den centrale grænsesætning er grundlaget for, hvordan normalfordelinger fungerer i statistik.
For at få et godt indtryk af en populations middelværdi skal man i forskning ideelt set indsamle data fra flere tilfældige stikprøver inden for populationen for at få et godt indtryk af en populations middelværdi. En stikprøvefordeling af middelværdien er fordelingen af middelværdierne for disse forskellige stikprøver.
Den centrale grænsesætning viser følgende:
- Lov of Large Numbers: Når du øger stikprøvestørrelsen (eller antallet af stikprøver), vil stikprøvens gennemsnit nærme sig populationens gennemsnit.
- Med flere store stikprøver er stikprøvefordelingen af gennemsnittet normalfordelt, selv om din oprindelige variabel ikke er normalfordelt.
Parametriske statistiske test antager typisk, at stikprøverne kommer fra normalfordelte populationer, men det centrale grænsesætningen betyder, at det ikke er nødvendigt at opfylde denne antagelse, når du har en tilstrækkelig stor stikprøve.
Du kan bruge parametriske test til store stikprøver fra populationer med enhver form for fordeling, så længe andre vigtige antagelser er opfyldt. En stikprøvestørrelse på 30 eller mere betragtes generelt som stor.
For små stikprøver er antagelsen om normalitet vigtig, fordi stikprøvefordelingen af middelværdien ikke er kendt. For at få nøjagtige resultater skal du være sikker på, at populationen er normalfordelt, før du kan bruge parametriske test med små stikprøver.
Formel for normalkurven
Når du har middelværdien og standardafvigelsen for en normalfordeling, kan du tilpasse en normalkurve til dine data ved hjælp af en sandsynlighedsdensitetsfunktion.


I en sandsynlighedsdensitetsfunktion fortæller arealet under kurven om sandsynligheden. Normalfordelingen er en sandsynlighedsfordeling, så det samlede areal under kurven er altid 1 eller 100 %.
Formlen for den normale sandsynlighedstæthedsfunktion ser ret kompliceret ud. Men for at bruge den behøver du kun at kende populationens middelværdi og standardafvigelse.
For en hvilken som helst værdi af x kan du indsætte middelværdien og standardafvigelsen i formlen for at finde sandsynlighedstætheden for den variabel, der antager den pågældende værdi af x.
| Normal sandsynlighedsdensitetsformel | Forklaring |
|---|---|
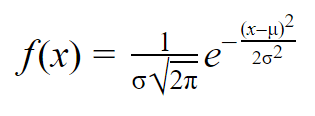 |
|
På din graf over sandsynlighedsdensitetsfunktionen er sandsynligheden det skraverede område under kurven, der ligger til højre for det sted, hvor din SAT-score er lig med 1380.


Du kan finde sandsynlighedsværdien for denne score ved hjælp af standardnormalfordelingen.
Hvad er standardnormalfordelingen?
Standardnormalfordelingen, også kaldet z-fordelingen, er en særlig normalfordeling, hvor middelværdien er 0, og standardafvigelsen er 1.
Alle normalfordelinger er en version af standardnormalfordelingen, der er blevet strakt eller presset og flyttet vandret til højre eller venstre.


Mens de enkelte observationer fra normalfordelinger betegnes som x, betegnes de som z i z-fordelingen. Enhver normalfordeling kan omdannes til standardnormalfordelingen ved at omdanne de enkelte værdier til z-scorer.
Z-scorer fortæller, hvor mange standardafvigelser fra middelværdien hver værdi ligger.


Du behøver kun at kende middelværdien og standardafvigelsen for din fordeling for at finde z-scoren for en værdi.
| Z-score Formel | Forklaring |
|---|---|
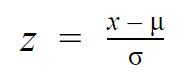 |
|
Vi omdanner normalfordelinger til standardnormalfordelingen af flere grunde:
- For at finde sandsynligheden for, at observationer i en fordeling falder over eller under en given værdi.
- For at finde sandsynligheden for, at et stikprøvegennemsnit afviger signifikant fra et kendt populationsgennemsnit.
- For at sammenligne resultater på forskellige fordelinger med forskellige gennemsnit og standardafvigelser.
Find sandsynlighed ved hjælp af z-fordelingen
Hver z-score er forbundet med en sandsynlighed, eller p-værdi, der fortæller dig sandsynligheden for, at der forekommer værdier under den pågældende z-score. Hvis du konverterer en individuel værdi til en z-score, kan du derefter finde sandsynligheden for, at alle værdier op til denne værdi forekommer i en normalfordeling.
Middelværdien af vores fordeling er 1150, og standardafvigelsen er 150. Z-scoren fortæller dig, hvor mange standardafvigelser 1380 er fra middelværdien.
| Formel | Beregning |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
For en z-score på 1,53 er p-værdien 0,937. Det er sandsynligheden for, at SAT-scoren er 1380 eller mindre (93,7 %), og det er arealet under kurven til venstre for det skraverede område.


For at finde det skraverede område tager man 0.937 fra 1, som er det samlede areal under kurven.
Sandsynligheden for x>1380 = 1 – 0,937 = 0,063
Det betyder, at det er sandsynligt, at kun 6,3 % af SAT-scorerne i din stikprøve overstiger 1380.
Hyppigt stillede spørgsmål om normalfordelinger
I en normalfordeling er data symmetrisk fordelt uden skævhed. De fleste værdier samler sig omkring et centralt område, og værdierne aftager i takt med, at de bevæger sig længere væk fra centrum.
Målene for central tendens (middelværdi, modus og median) er nøjagtig de samme i en normalfordeling.
Standardnormalfordelingen, også kaldet z-fordelingen, er en særlig normalfordeling, hvor middelværdien er 0 og standardafvigelsen er 1.
Alle normalfordelinger kan omdannes til standardnormalfordelingen ved at omdanne de enkelte værdier til z-værdier. I en z-fordeling fortæller z-scorerne, hvor mange standardafvigelser væk fra middelværdien hver værdi ligger.
Den empiriske regel, eller 68-95-99,7-reglen, fortæller dig, hvor de fleste værdier ligger i en normalfordeling:
- Omkring 68 % af værdierne ligger inden for 1 standardafvigelse fra middelværdien.
- Omkring 95 % af værdierne ligger inden for 2 standardafvigelser fra middelværdien.
- Omkring 99,7 % af værdierne ligger inden for 3 standardafvigelser fra gennemsnittet.
Den empiriske regel er en hurtig måde at få et overblik over dine data på og kontrollere, om der er outliers eller ekstreme værdier, der ikke følger dette mønster.
T-fordelingen er en måde at beskrive et sæt observationer på, hvor de fleste observationer falder tæt på middelværdien, og resten af observationerne udgør halerne på hver side. Det er en type normalfordeling, der anvendes til mindre stikprøver, hvor variansen i dataene er ukendt.
T-fordelingen danner en klokkeformet kurve, når den plottes på en graf. Den kan beskrives matematisk ved hjælp af middelværdien og standardafvigelsen.

