Logistisk regressionsanalyse

Udfaldet i logistisk regressionsanalyse er ofte kodet som 0 eller 1, hvor 1 angiver, at det ønskede udfald er til stede, og 0 angiver, at det ønskede udfald er fraværende. Hvis vi definerer p som sandsynligheden for, at resultatet er 1, kan den multiple logistiske regressionsmodel skrives som følger:

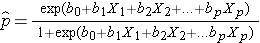
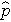er den forventede sandsynlighed for, at resultatet er til stede; X1 til Xp er særskilte uafhængige variabler; og b0 til bp er regressionskoefficienterne. Den multiple logistiske regressionsmodel skrives undertiden på en anden måde. I følgende form er udfaldet den forventede logaritme af sandsynligheden for, at udfaldet er til stede,

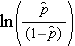
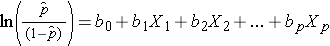
Bemærk, at højre side af ligningen ovenfor ligner den multiple lineære regressionsligning. Teknikken til estimering af regressionskoefficienterne i en logistisk regressionsmodel er imidlertid forskellig fra den teknik, der anvendes til at estimere regressionskoefficienterne i en multipel lineær regressionsmodel. I logistisk regression angiver de koefficienter, der er afledt af modellen (f.eks. b1), ændringen i de forventede log odds i forhold til en ændring på én enhed i X1, idet alle andre prædiktorer holdes konstante. Derfor giver antilog af en estimeret regressionskoefficient, exp(bi), et odds ratio, som illustreret i eksemplet nedenfor.

Eksempel på logistisk regression – sammenhæng mellem fedme og CVD

Vi har tidligere analyseret data fra en undersøgelse, der er designet til at vurdere sammenhængen mellem fedme (defineret som BMI > 30) og tilfældig kardiovaskulær sygdom. Data blev indsamlet fra deltagere, der var mellem 35 og 65 år, og som var fri for hjerte-kar-sygdomme (CVD) ved baseline. Hver deltager blev fulgt i 10 år med henblik på udvikling af kardiovaskulær sygdom. Et resumé af dataene findes på side 2 i dette modul. Den ujusterede eller rå relative risiko var RR = 1,78, og den ujusterede eller rå odds ratio var OR = 1,93. Vi fastslog også, at alder var en confounder, og ved hjælp af Cochran-Mantel-Haenszel-metoden estimerede vi en justeret relativ risiko på RRCMH =1,44 og et justeret odds ratio på ORCMH =1,52. Vi vil nu bruge logistisk regressionsanalyse til at vurdere sammenhængen mellem fedme og incidente kardiovaskulær sygdom justeret for alder.

Den logistiske regressionsanalyse afslører følgende:

Uafhængig variabel	Regressionskoefficient	Chi-kvadrat	P-værdi
Intercept	-2.367	307.38	0.0001
Obesity	0,658	9,87	0.0017

Den simple logistiske regressionsmodel relaterer fedme til log odds for incidente CVD:

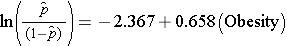
Fedme er en indikatorvariabel i modellen, der er kodet som følger: 1=overvægtig og 0=ikke overvægtig. Log-oddset for incidente CVD er 0,658 gange højere hos personer, der er overvægtige, sammenlignet med personer, der ikke er overvægtige. Hvis vi tager antilog af regressionskoefficienten, exp(0,658) = 1,93, får vi det rå eller ujusterede odds ratio. Oddset for at udvikle CVD er 1,93 gange højere blandt overvægtige personer sammenlignet med ikke-overvægtige personer. Sammenhængen mellem fedme og tilfældig CVD er statistisk signifikant (p=0,0017). Bemærk, at teststatistikken til vurdering af regressionsparametrenes signifikans i logistisk regressionsanalyse er baseret på chi-kvadratstatistik i modsætning til t-statistik, som det var tilfældet med lineær regressionsanalyse. Dette skyldes, at der anvendes en anden estimationsteknik, kaldet maximum likelihood estimation, til at estimere regressionsparametrene (se Hosmer og Lemeshow3 for tekniske detaljer).

Mange statistiske datapakker genererer også odds ratio’er samt 95 % konfidensintervaller for odds ratio’erne som en del af deres logistiske regressionsanalyseprocedure. I dette eksempel er estimatet af odds ratio 1,93, og 95 % konfidensintervallet er (1,281, 2,913).

Ved undersøgelsen af sammenhængen mellem fedme og CVD har vi tidligere fastslået, at alder var en confounder.Den følgende multiple logistiske regressionsmodel estimerer sammenhængen mellem fedme og tilfældig CVD, idet der justeres for alder. I modellen tager vi igen hensyn til to aldersgrupper (mindre end 50 år og 50 år og derover). I analysen er aldersgruppen kodet på følgende måde: 1=50 år og derover og 0=mindre end 50 år.

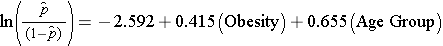
Hvis vi tager antilogen af regressionskoefficienten forbundet med fedme, exp(0,415) = 1,52, får vi odds ratio justeret for alder. Oddset for at udvikle CVD er 1,52 gange højere blandt overvægtige personer sammenlignet med ikke-overvægtige personer, justeret for alder. I afsnit 9.2 anvendte vi Cochran-Mantel-Haenszel-metoden til at generere et odds ratio justeret for alder og fandt følgende:

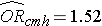
Dette illustrerer, hvordan multipel logistisk regressionsanalyse kan anvendes til at tage højde for forvirrende faktorer. Modellerne kan udvides til at tage højde for flere forstyrrende variabler samtidig. Multipel logistisk regressionsanalyse kan også anvendes til at vurdere confounding og effektmodifikation, og fremgangsmåderne er identiske med dem, der anvendes i multipel lineær regressionsanalyse. Multipel logistisk regressionsanalyse kan også anvendes til at undersøge virkningen af flere risikofaktorer (i modsætning til at fokusere på en enkelt risikofaktor) på et dikotomt udfald.

Eksempel – risikofaktorer forbundet med lav fødselsvægt hos spædbørn

Sæt, at undersøgerne også beskæftiger sig med negative graviditetsudfald, herunder gestationel diabetes, præeklampsi (dvs. graviditetsinduceret hypertension) og for tidlig fødsel. Husk på, at undersøgelsen omfattede 832 gravide kvinder, der leverer demografiske og kliniske data. I undersøgelsens stikprøve udvikler 22 (2,7 %) kvinder præeklampsi, 35 (4,2 %) udvikler svangerskabsdiabetes og 40 (4,8 %) udvikler præterm fødsel. Lad os antage, at vi ønsker at vurdere, om der er forskelle i hvert af disse negative graviditetsudfald efter race/etnicitet, justeret for moderens alder. Der blev gennemført tre separate logistiske regressionsanalyser, der relaterede hvert resultat, betragtet separat, til de tre dummy- eller indikatorvariabler, der afspejler moderens race og moderens alder i år. Resultaterne er anført nedenfor.

Udgang: Præeklampsi	Regressionskoefficient	Chi-square	P-værdi	Odds Ratio (95% CI)
Intercept	-3.066	4.518	0.0335	–
Sort race	2.191	12.640	0.0004	8.948 (2.673, 29.949)
Hispanisk race	-0.1053	0.0325	0.8570	0.8570	0.900 (0,286, 2,829)
Andre race	0,0586	0,0021	0,0021	0.9046	1.060 (0.104, 3.698)
Mødrenes alder (år)	-0.0252	0.3574	0,5500	0,975 (0,898, 1,059)

Den eneste statistisk signifikante forskel i præeklampsi er mellem sorte og hvide mødre.

Sorte mødre har næsten 9 gange større risiko for at udvikle præeklampsi end hvide mødre, justeret for mødrenes alder. 95 % konfidensintervallet for odds ratio ved sammenligning af sorte versus hvide kvinder, der udvikler præeklampsi, er meget bredt (2,673 til 29,949). Dette skyldes det faktum, at der er et lille antal udfaldsbegivenheder (kun 22 kvinder udvikler præeklampsi i den samlede stikprøve) og et lille antal kvinder af sort race i undersøgelsen. Derfor bør denne association fortolkes med forsigtighed.

Mens odds ratio er statistisk signifikant, antyder konfidensintervallet, at størrelsen af effekten kan være alt fra en 2,6-dobbelt stigning til en 29,9-dobbelt stigning. Der er behov for en større undersøgelse for at generere et mere præcist estimat af effekten.

Gestationel diabetes	Regressionskoefficient	Chi-square	P-værdi	Odds Ratio (95% CI)
Intercept	-5.823	22,968	0,0001	–
Sort race	1,621	6.660	0,0099	5,056 (1,477, 17,312)
Hispanisk race	0,581	1.766	0.1839	1.787 (0.759, 4.207)
Andre race	1.348	5.917	0.0150	3.848 (1.299, 11.395)
Moderens alder (år)	0.071	4.314	0,0378	1,073 (1,004, 1,147)

Med hensyn til svangerskabsdiabetes er der statistisk signifikante forskelle mellem sorte og hvide mødre (p=0,0099) og mellem mødre, der identificerer sig selv som anden race sammenlignet med hvide (p=0,0150), justeret for moderens alder. Moderens alder er også statistisk signifikant (p=0,0378), idet ældre kvinder har større sandsynlighed for at udvikle svangerskabsdiabetes, justeret for race/etnicitet.

Resultat: For tidlig fødsel	Regressionskoefficient	Chi-kvadrat	P-værdi	Odds Ratio (95% CI)
Intercept	-1.443	1.602	0.2056	–
Sort race	-0,082	0,015	0,015	0.9039	0,921 (0,244, 3,483)
Hispanisk race	-1,564	9.497	0,0021	0,209 (0,077, 0,566)
Andre race	0.548	1.124	0.2890	1.730 (0.628,4.767)
Moderens alder (åre.)	00,037	1,198	0,2737	0,963 (0,901, 1,030)

Med hensyn til fødsel før termin er den eneste statistisk signifikante forskel mellem latinamerikanske og hvide mødre (p=0,0021). Hispaniske mødre har 80 % mindre sandsynlighed for at udvikle præterm fødsel end hvide mødre (odds ratio = 0,209), justeret for moderens alder.

Multivariable metoder er beregningsteknisk komplekse og kræver generelt brug af en statistisk datapakke. Multivariable metoder kan bruges til at vurdere og justere for forvirring, til at afgøre, om der er effekt modifikation, eller til at vurdere forholdet mellem flere eksponerings- eller risikofaktorer på et resultat samtidig. Multivariable analyser er komplekse og bør altid planlægges, så de afspejler biologisk plausible forhold. Selv om det er relativt nemt at overveje en ekstra variabel i en multipel lineær eller multipel logistisk regressionsmodel, bør kun variabler, der er klinisk meningsfulde, medtages.

Det er vigtigt at huske, at multivariable modeller kun kan justere eller tage højde for forskelle i forstyrrende variabler, der blev målt i undersøgelsen. Desuden bør multivariable modeller kun anvendes til at tage højde for forvirring, når der er et vist overlap i fordelingen af den forvirrende faktor i hver af risikofaktorgrupperne.

Stratificerede analyser er meget informative, men hvis prøverne i specifikke strata er for små, kan analyserne mangle præcision. Ved planlægning af undersøgelser skal investigatorerne være omhyggelige med at være opmærksomme på potentielle effektmodifikatorer. Hvis der er mistanke om, at en sammenhæng mellem en eksponering eller en risikofaktor er forskellig i bestemte grupper, skal undersøgelsen udformes således, at der sikres et tilstrækkeligt antal deltagere i hver af disse grupper. Der skal anvendes stikprøvestørrelsesformler til at bestemme det antal forsøgspersoner, der kræves i hvert stratum for at sikre tilstrækkelig præcision eller effekt i analysen.

retur til toppen | forrige side | næste side