Enkle beskrivelse
Lad os først se på pi-bindingen i ethen ud fra et forenklet MO-teoretisk synspunkt (i dette eksempel ser vi bort fra sigma-bindingerne i molekylet og tænker kun på π-bindingen). Vi starter med to atomorbitaler: en uhybridiseret 2p-orbital fra hvert kulstof. Hver indeholder en enkelt elektron. I MO-teorien kombineres de to atomare matematisk for at danne to pi-molekylære orbitaler, et pi-bindingsorbital med lav energi og et pi*-antibindingsorbital med høj energi.

Molekylorbitaler for ethen (ethylen)
I den bindende pi-orbital interagerer de to skraverede lapper af p-orbitalerne konstruktivt med hinanden, ligesom de to u-skraverede lapper (husk, at det vilkårlige valg af skravering repræsenterer matematiske (+) og (-) tegn for den matematiske bølgefunktion, der beskriver orbitalet). Der er øget elektrontæthed mellem de to kulstofkerner i den molekylære orbital – det er en bindingsvekselvirkning.
I den højere energimæssige antibindende pi*-orbital vekselvirker den skraverede lobe af den ene p-orbital destruktivt med den uskraverede lobe af den anden p-orbital, hvilket fører til et knudepunkt mellem de to kerner og en generel frastødning mellem kulstofkernerne.
Igen ved hjælp af “opbygningsprincippet” placerer vi de to elektroner i den lavere energimæssige, bindende pi-molekylorbital. Den antibindende pi*-orbital forbliver tom.
Mere detaljeret MO-beskrivelse af ethen
Molekylorbitalteori er med stor succes blevet anvendt på store konjugerede systemer, især dem, der indeholder kæder af kulstofatomer med skiftevis enkelt- og dobbeltbindinger. En tilnærmelse, der blev indført af Hückel i 1931, tager kun hensyn til de delokaliserede p-elektroner, der bevæger sig i en ramme af \pi -bindinger. Dette er i virkeligheden en mere sofistikeret udgave af en model med frie elektroner. I et introduktionskursus i organisk kemi er det ikke nødvendigt at bruge hele Hückels matematik, men for dem, der gerne vil dykke dybere ned, gives en mere detaljeret analyse her.
Den enkleste kulbrinte, der udviser \pi-binding, er ethen (ethylen), som består af fire hydrogenatomer og to kulstofatomer. Eksperimentelt ved vi, at H-C-H- og H-C-C-C-vinklerne i ethen er ca. 120°. Denne vinkel tyder på, at kulstofatomerne er sp2-hybridiserede, hvilket betyder, at et enkelt besat sp2-orbital på det ene kulstof overlapper med et enkelt besat s-orbital på hvert H og en enkelt besat sp2-lob på det andet C. Hvert kulstof danner således et sæt af tre \sigmabindinger: to C-H (sp2 + s) og et C-C (sp2 + sp2) (del (a) af figur 13.1. nedenfor).

Figur 13.1. (a) Den σ-bundne ramme er dannet ved overlapning af to sæt enkeltbesatte kulstof sp2 hybridorbitaler og fire enkeltbesatte hydrogen 1s orbitaler for at danne elektronparbindinger. Herved anvendes 10 af de 12 valenselektroner til at danne i alt fem σ-bindinger (fire C-H-bindinger og en C-C-binding). (b) En enkelt besat uhybridiseret 2pz-orbital forbliver på hvert kulstofatom for at danne en π-binding mellem kulstof og kulstof. (Bemærk: Ved plane molekyler er den akse, der er vinkelret på molekylplanet, konventionelt set z-aksen.)
Hückel-approksimationen anvendes til at bestemme energierne og formen af \pi-molekylorbitalerne i konjugerede systemer. Inden for Hückel-approksimationen kan den kovalente binding i disse kulbrinter opdeles i to uafhængige “rammer”: \sigma -bindingsrammen og \sigma -bindingsrammen. De bølgefunktioner, der anvendes til at beskrive bindingsorbitalerne i hver ramme, er resultatet af forskellige kombinationer af atomorbitaler. Metoden begrænser sig til at behandle konjugerede kulbrinter, og specifikt er kun \pi-elektronernes molekylære orbitaler medtaget, fordi disse bestemmer de generelle egenskaber ved disse molekyler; sigma-elektronerne er ignoreret. Dette kaldes sigma-pi-separabilitet og er begrundet i ortogonaliteten mellem \sigma- og \pi-orbitalerne i plane molekyler. Af denne grund er Hückel-metoden begrænset til planare systemer. Hückel-approximationen antager, at elektronerne i \pi-bindingerne “føler” et elektrostatisk potentiale som følge af hele \sigma-bindingsrammen i molekylet (dvs. den fokuserer kun på dannelsen af \pi-bindinger, da \sigma-bindingsrammen allerede er blevet dannet).
Konjugerede systemer
Et konjugeret system har et område med overlappende p-orbitaler, der bygger bro over de indbyrdes forbundne enkeltbindinger, og som tillader en delokalisering af \pi-elektroner på tværs af alle de tilstødende justerede p-orbitaler. Disse \pi-elektroner tilhører ikke en enkelt binding eller et enkelt atom, men snarere en gruppe af atomer.
Ethen
Hvor vi overvejer Hückel-behandlingen for ethen, er det en fordel at gennemgå det generelle bindingsbillede af molekylet. Bindingen i ethen indebærer sp^2-hybridisering af 2s , 2p_x og 2p_y-atomorbitalerne på hvert kulstofatom; 2p_z-orbitalerne forbliver uberørte (figur 13.2).
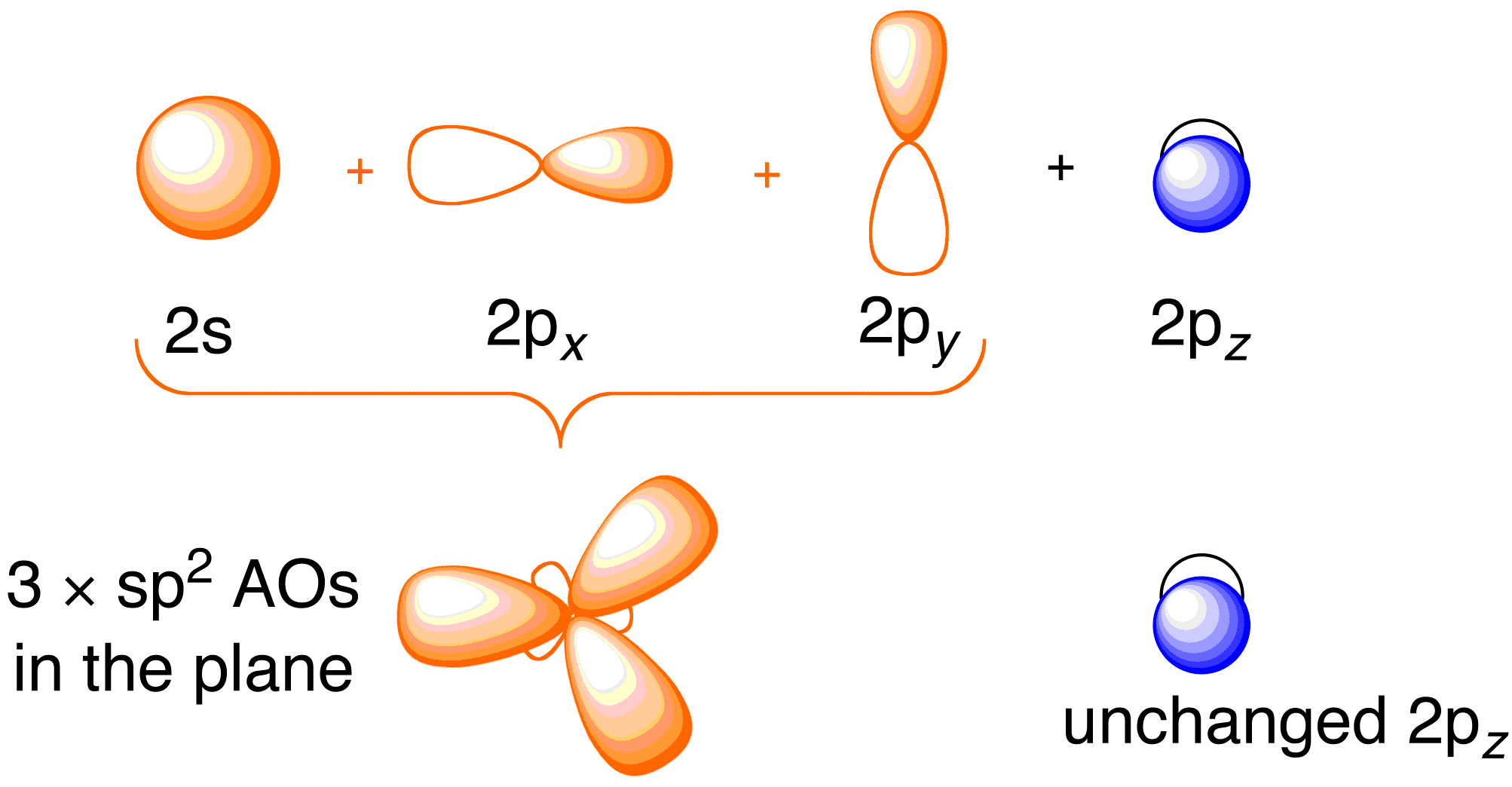
Figur 13.2. Hybridisering af kulstofatomorbitalerne for at give sp^2-hybridorbitaler til binding til hydrogenatomer i ethen. Billede anvendt med tilladelse fra ChemTube (CC-SA-BY-NC; Nick Greeves).
Brugen af hybridorbitaler i den molekylære orbitaltilgang, der beskrives her, er blot en bekvemmelighed og påberåber sig ikke valensbindingsteori (direkte). En identisk beskrivelse kan udtrækkes ved udelukkende atombaserede orbitaler på kulstof, men fortolkningen af de resulterende bølgefunktioner er mindre intuitiv. F.eks. kan den i’te molekylære orbital beskrives via hybridorbitaler
\
eller via atomorbitaler.
\
hvor \{a_i\} og \{c_i\} er koefficienter for ekspansionen. Begge beskrivelser vil fungere, og begge er identiske fremgangsmåder, da
\
hvor \{c_i\} er koefficienter, der beskriver den hybridiserede orbital.
Bindingen sker via blandingen af elektronerne i sp^2-hybridorbitalerne på kulstof og elektronerne i 1s atomorbitalerne på de fire brintatomer (figur 13.2. ovenfor til venstre), hvilket resulterer i \sigma -bindingsrammen. \pi -bindingsrammen er resultatet af de uhybridiserede 2p_z-orbitaler (figur 13.2. ovenfor, til højre). Uafhængigheden af disse to rammer fremgår af det resulterende molekylære orbitaldiagram i figuren nedenfor; Hückel-teorien beskæftiger sig kun med at beskrive de molekylære orbitaler og energier i \pi-bindingsrammen.

Figur 13.3: Molekylære orbitaler, der demonstrerer sigma-pi-adskilleligheden af \pi -bindingsrammen (blå) og \sigma -bindingsrammerne (rød) for ethylen.
Hückel-behandlingen beskæftiger sig kun med at beskrive de molekylære orbitaler og energier i \pi-bindingsrammen.
Da Hückel-teorien er en særlig betragtning af molekylorbitalteorien, kan molekylorbitalerne | \psi_i \rangle beskrives som en lineær kombination af 2p_z-atomorbitalerne \phi ved carbon med deres tilsvarende \{c_i\}-koefficienter:
\
For den komplette kvantekemiske analyse ved hjælp af Schrödinger-ligningen (ikke påkrævet i organisk kemi), se denne Libretexts-side.
Disse molekylære orbitaler danner π-bindingsrammen, og da hvert kulstof bidrager med én elektron til denne ramme, er kun den laveste molekylære orbital ( | \psi_1 \rangle ) besat (figur ) i grundtilstanden. Den tilsvarende elektronkonfiguration er så \pi_1^2 .

Figur 13.4: Skematisk repræsentation af \pi-molekylorbitalrammen for ethylen . Bemærk, at den antibindende molekylorbital har én knude mere end den bindende molekylorbital som forventet, da den har en højere energi.
HOMO og LUMO er akronymer for henholdsvis højeste besatte molekylorbital og laveste ubesatte molekylorbital og omtales ofte som grænseorbitaler. Energiforskellen mellem HOMO og LUMO betegnes HOMO-LUMO-gapet.
De 3D-beregnede \pi-molekylorbitaler er vist i figur 13.5.

Figur 13.5: Beregnede \pi-molekylorbitaler for ethylen . (til venstre) den bindende orbital (ψ1) og (til højre) den antibindende (ψ2) orbital.
Medvirkende
- Seymour Blinder (professor emeritus i kemi og fysik ved University of Michigan, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
