En trekant med en retvinklet vinkel kaldes en retvinklet trekant. Den side, der ligger over for den rette vinkel, kaldes trekantens hypotenuse. De to andre sider kaldes ben. De to andre vinkler har ikke noget særligt navn, men de er altid komplementære. Kan du se hvorfor? Den samlede vinkelsummen i en trekant er 180 grader, og den rette vinkel er 90 grader, så de to andre må summen være 90 grader.
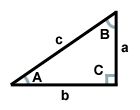
Den ovenstående trekant har siden c som hypotenuse, siderne a og b som ben og vinkel C som den rette vinkel. Vinklerne A og B er komplementære.
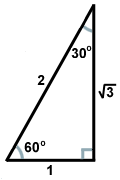
Der findes to typer af retvinklede trekanter, som enhver matematiker bør kende meget godt. Den ene er den retvinklede trekant, der dannes, når man trækker en højde fra et toppunkt i en ligesidet trekant, hvorved der dannes to kongruente retvinklede trekanter. Vinklerne i trekanten vil være 30, 60 og 90 grader, hvilket har givet trekanten sit navn: 30-60-90 trekanten. Forholdet mellem sidelængderne i sådanne trekanter er altid det samme: hvis benet over for den 30 graders vinkel er af længde x, vil benet over for den 60 graders vinkel være af længde x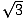
, og hypotenusen over for den rette vinkel vil være 2x. Her er en 30-60-90 trekant afbilledet nedenfor.
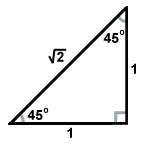
Den anden almindelige retvinklede trekant er resultatet af det trekantpar, der opstår, når en diagonal deler et kvadrat i to trekanter. Hver af disse trekanter er kongruente og har vinkler med målene 45, 45 og 90 grader. Hvis benene over for de 45 graders vinkler har en længde x, har hypotenusen en længde på x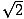
. Dette forhold gælder for alle 45-45-90 trekanter. 45-45-90 trekanter kaldes også ofte ligebenede retvinklede trekanter.
En sidste egenskab, der skal bemærkes, er, at benene i en retvinklet trekant også er højder i trekanten. Derfor er arealet af en retvinklet trekant halvdelen af produktet af længderne af benene.