Logistische Regressionsanalyse

Das Ergebnis in der logistischen Regressionsanalyse wird oft als 0 oder 1 kodiert, wobei 1 bedeutet, dass das interessierende Ergebnis vorhanden ist, und 0 bedeutet, dass das interessierende Ergebnis nicht vorhanden ist. Wenn wir p als die Wahrscheinlichkeit definieren, dass das Ergebnis 1 ist, kann das multiple logistische Regressionsmodell wie folgt geschrieben werden:

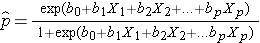
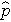ist die erwartete Wahrscheinlichkeit, dass das Ergebnis vorhanden ist; X1 bis Xp sind verschiedene unabhängige Variablen; und b0 bis bp sind die Regressionskoeffizienten. Das Modell der multiplen logistischen Regression wird manchmal anders geschrieben. In der folgenden Form ist das Ergebnis der erwartete Logarithmus der Wahrscheinlichkeit, dass das Ergebnis vorhanden ist,

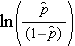
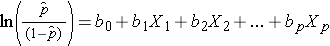
Beachten Sie, dass die rechte Seite der obigen Gleichung wie die multiple lineare Regressionsgleichung aussieht. Die Technik zur Schätzung der Regressionskoeffizienten in einem logistischen Regressionsmodell unterscheidet sich jedoch von derjenigen, die zur Schätzung der Regressionskoeffizienten in einem multiplen linearen Regressionsmodell verwendet wird. Bei der logistischen Regression geben die aus dem Modell abgeleiteten Koeffizienten (z. B. b1) die Änderung der erwarteten logarithmischen Chancen im Verhältnis zu einer Änderung von X1 um eine Einheit an, wobei alle anderen Prädiktoren konstant bleiben. Daher ergibt der Antilog eines geschätzten Regressionskoeffizienten, exp(bi), ein Odds Ratio, wie im folgenden Beispiel dargestellt.

Beispiel für logistische Regression – Zusammenhang zwischen Adipositas und kardiovaskulären Erkrankungen

Wir haben zuvor Daten aus einer Studie analysiert, die den Zusammenhang zwischen Adipositas (definiert als BMI > 30) und kardiovaskulären Erkrankungen untersuchen sollte. Die Daten wurden von Teilnehmern erhoben, die zwischen 35 und 65 Jahre alt waren und bei Studienbeginn keine Herz-Kreislauf-Erkrankungen aufwiesen. Jeder Teilnehmer wurde 10 Jahre lang hinsichtlich der Entwicklung von Herz-Kreislauf-Erkrankungen beobachtet. Eine Zusammenfassung der Daten finden Sie auf Seite 2 dieses Moduls. Das unbereinigte oder grobe relative Risiko betrug RR = 1,78, und das unbereinigte oder grobe Odds Ratio betrug OR = 1,93. Wir stellten außerdem fest, dass das Alter ein Störfaktor ist, und schätzten mithilfe der Cochran-Mantel-Haenszel-Methode ein bereinigtes relatives Risiko von RRCMH =1,44 und ein bereinigtes Odds Ratio von ORCMH =1,52. Wir werden nun eine logistische Regressionsanalyse verwenden, um den Zusammenhang zwischen Adipositas und dem Auftreten von Herz-Kreislauf-Erkrankungen unter Berücksichtigung des Alters zu bewerten.

Die logistische Regressionsanalyse zeigt Folgendes:

Unabhängige Variable	Regressionskoeffizient	Chi-square	P-value
Intercept	-2.367	307.38	0.0001
Fettsucht	0.658	9.87	0.0017

Das einfache logistische Regressionsmodell setzt Adipositas mit der logarithmischen Wahrscheinlichkeit eines CVD-Inzidenzereignisses in Beziehung:

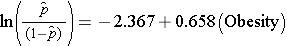
Adipositas ist eine Indikatorvariable in dem Modell, die wie folgt kodiert ist: 1=fettleibig und 0=nicht fettleibig. Die logarithmische Wahrscheinlichkeit, an einer CVD zu erkranken, ist bei fettleibigen Personen 0,658 Mal höher als bei nicht fettleibigen Personen. Nimmt man den Antilog des Regressionskoeffizienten, exp(0,658) = 1,93, so erhält man das rohe oder nicht bereinigte Odds Ratio. Die Wahrscheinlichkeit, an einer CVD zu erkranken, ist bei fettleibigen Personen 1,93 Mal höher als bei nicht fettleibigen Personen. Der Zusammenhang zwischen Fettleibigkeit und dem Auftreten von CVD ist statistisch signifikant (p=0,0017). Es ist zu beachten, dass die Teststatistiken zur Bewertung der Signifikanz der Regressionsparameter in der logistischen Regressionsanalyse auf Chi-Quadrat-Statistiken basieren, im Gegensatz zu t-Statistiken wie bei der linearen Regressionsanalyse. Dies liegt daran, dass zur Schätzung der Regressionsparameter ein anderes Schätzverfahren, die so genannte Maximum-Likelihood-Schätzung, verwendet wird (siehe Hosmer und Lemeshow3 für technische Einzelheiten).

Viele statistische Datenverarbeitungspakete erzeugen im Rahmen ihrer logistischen Regressionsanalyse auch Odds Ratios sowie 95%-Konfidenzintervalle für die Odds Ratios. In diesem Beispiel beträgt das geschätzte Odds Ratio 1,93 und das 95%-Konfidenzintervall (1,281, 2,913).

Bei der Untersuchung des Zusammenhangs zwischen Adipositas und CVD haben wir zuvor festgestellt, dass das Alter ein Störfaktor ist.

Das folgende Modell der multiplen logistischen Regression schätzt den Zusammenhang zwischen Adipositas und neu auftretender CVD unter Berücksichtigung des Alters. In dem Modell werden wiederum zwei Altersgruppen berücksichtigt (unter 50 Jahre und 50 Jahre und älter). Für die Analyse wird die Altersgruppe wie folgt kodiert: 1=50 Jahre und älter und 0=weniger als 50 Jahre.

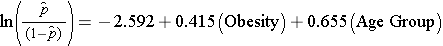
Nimmt man den Antilog des Regressionskoeffizienten in Verbindung mit Adipositas, exp(0,415) = 1,52, so erhält man das um das Alter bereinigte Odds Ratio. Die Wahrscheinlichkeit, an einer CVD zu erkranken, ist bei fettleibigen Personen im Vergleich zu nicht fettleibigen Personen 1,52-mal höher, wenn man das Alter berücksichtigt. In Abschnitt 9.2 haben wir die Cochran-Mantel-Haenszel-Methode angewandt, um ein altersbereinigtes Odds Ratio zu erstellen, und dabei Folgendes herausgefunden:

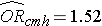
Dies veranschaulicht, wie die multiple logistische Regressionsanalyse zur Berücksichtigung von Störfaktoren verwendet werden kann. Die Modelle können erweitert werden, um mehrere Störvariablen gleichzeitig zu berücksichtigen. Die multiple logistische Regressionsanalyse kann auch zur Bewertung von Confounding und Effektmodifikation verwendet werden, und die Ansätze sind identisch mit denen der multiplen linearen Regressionsanalyse. Die multiple logistische Regressionsanalyse kann auch verwendet werden, um die Auswirkungen mehrerer Risikofaktoren (im Gegensatz zur Konzentration auf einen einzelnen Risikofaktor) auf ein dichotomes Ergebnis zu untersuchen.

Beispiel – Risikofaktoren im Zusammenhang mit niedrigem Geburtsgewicht

Angenommen, die Forscher befassen sich auch mit negativen Schwangerschaftsergebnissen wie Schwangerschaftsdiabetes, Präeklampsie (d. h. schwangerschaftsbedingter Bluthochdruck) und vorzeitigen Wehen. Es sei daran erinnert, dass an der Studie 832 schwangere Frauen teilnahmen, die demografische und klinische Daten lieferten. In der Stichprobe der Studie entwickelten 22 (2,7 %) Frauen eine Präeklampsie, 35 (4,2 %) einen Schwangerschaftsdiabetes und 40 (4,8 %) eine vorzeitige Geburt. Nehmen wir an, wir möchten beurteilen, ob es Unterschiede bei jeder dieser negativen Schwangerschaftsfolgen nach Rasse/ethnischer Zugehörigkeit gibt, bereinigt um das mütterliche Alter. Es wurden drei getrennte logistische Regressionsanalysen durchgeführt, die jedes Ergebnis, separat betrachtet, mit den drei Dummy- oder Indikatorvariablen in Beziehung setzten, die die Rasse der Mutter und das Alter der Mutter in Jahren widerspiegeln. Die Ergebnisse sind unten aufgeführt.

Ergebnis: Präeklampsie	Regressionskoeffizient	Chi-square	P-value	Odds Ratio (95% CI)
Intercept	-3.066	4.518	0.0335	–
Schwarze Rasse	2.191	12.640	0.0004	8.948 (2.673, 29.949)
Hispanische Rasse	-0.1053	0.0325	0.8570	0.900 (0.286, 2.829)
Andere Rasse	0.0586	0.0021	0.9046	1,060 (0,104, 3,698)
Alter der Mutter (Jg.)	-0,0252	0.3574	0,5500	0,975 (0,898, 1,059)

Der einzige statistisch signifikante Unterschied bei der Präeklampsie besteht zwischen schwarzen und weißen Müttern.

Schwarze Mütter haben eine fast 9-mal höhere Wahrscheinlichkeit, eine Präeklampsie zu entwickeln als weiße Mütter, bereinigt um das mütterliche Alter. Das 95 %-Konfidenzintervall für das Odds Ratio zwischen schwarzen und weißen Frauen, die eine Präeklampsie entwickeln, ist sehr breit (2,673 bis 29,949). Dies ist darauf zurückzuführen, dass es nur eine kleine Anzahl von Endpunkten gibt (nur 22 Frauen entwickeln eine Präeklampsie in der Gesamtstichprobe) und eine kleine Anzahl von Frauen schwarzer Hautfarbe in der Studie. Daher sollte diese Assoziation mit Vorsicht interpretiert werden.

Während das Odds Ratio statistisch signifikant ist, deutet das Konfidenzintervall darauf hin, dass das Ausmaß des Effekts zwischen einem 2,6-fachen und einem 29,9-fachen Anstieg liegen könnte. Eine größere Studie ist erforderlich, um eine genauere Schätzung der Wirkung zu erhalten.

Gestationsdiabetes	Regressionskoeffizient	Chi-Quadrat	P-Wert	Odds Ratio (95% CI)
Intercept	-5.823	22.968	0.0001	–
Schwarze Rasse	1.621	6.660	0,0099	5,056 (1,477, 17,312)
Hispanische Rasse	0,581	1.766	0,1839	1,787 (0,759, 4,207)
Andere Rasse	1,348	5.917	0.0150	3.848 (1.299, 11.395)
Alter der Mutter (Jg.)	0.071	4.314	0,0378	1,073 (1,004, 1,147)

In Bezug auf Schwangerschaftsdiabetes gibt es statistisch signifikante Unterschiede zwischen schwarzen und weißen Müttern (p=0,0099) und zwischen Müttern, die sich selbst als andere Rasse identifizieren, im Vergleich zu weißen (p=0,0150), bereinigt um das Alter der Mutter. Das Alter der Mutter ist ebenfalls statistisch signifikant (p=0,0378), wobei ältere Frauen mit größerer Wahrscheinlichkeit Schwangerschaftsdiabetes entwickeln, bereinigt um Rasse/Ethnizität.

Ergebnis: Frühgeburt	Regressionskoeffizient	Chi-square	P-value	Odds Ratio (95% CI)
Intercept	-1.443	1.602	0.2056	–
Schwarze Rasse	-0.082	0.015	0.9039	0,921 (0,244, 3,483)
Hispanische Rasse	-1,564	9.497	0.0021	0.209 (0.077, 0.566)
Andere Rasse	0.548	1.124	0.2890	1.730 (0.628,4.767)
Alter der Mutter (Jgst.)	00,037	1,198	0,2737	0,963 (0,901, 1,030)

Bezüglich der Wehen vor der Geburt besteht der einzige statistisch signifikante Unterschied zwischen hispanischen und weißen Müttern (p=0,0021). Bei hispanischen Müttern ist die Wahrscheinlichkeit, vorzeitige Wehen zu bekommen, um 80 % geringer als bei weißen Müttern (Odds Ratio = 0,209), bereinigt um das Alter der Mutter.

Multivariable Methoden sind rechnerisch komplex und erfordern in der Regel den Einsatz eines statistischen Datenverarbeitungsprogramms. Multivariable Methoden können verwendet werden, um Verunreinigungen zu bewerten und zu bereinigen, um festzustellen, ob es eine Veränderung des Effekts gibt, oder um die Beziehungen zwischen mehreren Expositions- oder Risikofaktoren auf ein Ergebnis gleichzeitig zu bewerten. Multivariable Analysen sind komplex und sollten immer so geplant werden, dass sie biologisch plausible Zusammenhänge widerspiegeln. Es ist zwar relativ einfach, eine zusätzliche Variable in einem multiplen linearen oder multiplen logistischen Regressionsmodell zu berücksichtigen, doch sollten nur Variablen einbezogen werden, die klinisch bedeutsam sind.

Es ist wichtig, daran zu denken, dass multivariable Modelle nur Unterschiede bei Störvariablen, die in der Studie gemessen wurden, anpassen oder berücksichtigen können. Außerdem sollten multivariable Modelle nur dann zur Berücksichtigung von Störfaktoren verwendet werden, wenn es eine gewisse Überschneidung in der Verteilung der Störfaktoren in den einzelnen Risikofaktorgruppen gibt.

Stratifizierte Analysen sind sehr informativ, aber wenn die Stichproben in bestimmten Schichten zu klein sind, können die Analysen ungenau sein. Bei der Planung von Studien müssen die Untersucher sorgfältig auf potenzielle Effektmodifikatoren achten. Wenn der Verdacht besteht, dass ein Zusammenhang zwischen einer Exposition oder einem Risikofaktor in bestimmten Gruppen unterschiedlich ist, muss die Studie so angelegt werden, dass eine ausreichende Anzahl von Teilnehmern in jeder dieser Gruppen gewährleistet ist. Es müssen Formeln für den Stichprobenumfang verwendet werden, um die Anzahl der Probanden zu bestimmen, die in jeder Schicht erforderlich sind, um eine angemessene Genauigkeit oder Aussagekraft der Analyse zu gewährleisten.

Zum Anfang zurückkehren | vorherige Seite | nächste Seite