Einfache Beschreibung
Betrachten wir zunächst die pi-Bindung in Ethen aus der Sicht einer vereinfachten MO-Theorie (in diesem Beispiel lassen wir die Sigma-Bindungen im Molekül außer Acht und denken nur an die π-Bindung). Wir beginnen mit zwei Atomorbitalen: ein unhybridisiertes 2p-Orbital von jedem Kohlenstoff. Jedes enthält ein einzelnes Elektron. In der MO-Theorie verbinden sich die beiden Atomorbitale mathematisch zu zwei pi-Molekülorbitalen, einem energiearmen pi-Bindungsorbital und einem energiereichen pi*-Antibindungsorbital.

Molekülorbitale für Ethen (Ethylen)
Im bindenden pi-Orbital stehen die beiden schattierten Lappen der p-Orbitale in konstruktiver Wechselwirkung miteinander, ebenso wie die beiden nicht schattierten Lappen (zur Erinnerung: die willkürliche Wahl der Schattierung steht für mathematische (+) und (-) Zeichen der mathematischen Wellenfunktion, die das Orbital beschreibt). Es besteht eine erhöhte Elektronendichte zwischen den beiden Kohlenstoffkernen im Molekülorbital – es handelt sich um eine bindende Wechselwirkung.
Im energiereichen, antibindenden pi*-Orbital interagiert der schattierte Lappen des einen p-Orbitals destruktiv mit dem nicht schattierten Lappen des zweiten p-Orbitals, was zu einem Knoten zwischen den beiden Kernen und einer allgemeinen Abstoßung zwischen den Kohlenstoffkernen führt.
Wiederum nach dem „Aufbauprinzip“ platzieren wir die beiden Elektronen in das energieärmere, bindende pi-Molekülorbital. Das antibindende pi*-Orbital bleibt leer.
Detailliertere MO-Beschreibung von Ethen
Die Molekülorbitaltheorie wurde sehr erfolgreich auf große konjugierte Systeme angewandt, insbesondere auf solche, die Ketten von Kohlenstoffatomen mit abwechselnden Einfach- und Doppelbindungen enthalten. Eine von Hückel 1931 eingeführte Näherung berücksichtigt nur die delokalisierten p-Elektronen, die sich in einem Rahmen von \pi -Bindungen bewegen. Dabei handelt es sich um eine verfeinerte Version eines Modells mit freien Elektronen. Für einen Einführungskurs in die organische Chemie brauchen wir nicht die gesamte Mathematik von Hückel zu verwenden, aber für diejenigen, die tiefer eindringen wollen, wird hier eine detailliertere Analyse gegeben.
Der einfachste Kohlenwasserstoff, der \pi-Bindungen aufweist, ist Ethen (Ethylen), das aus vier Wasserstoffatomen und zwei Kohlenstoffatomen besteht. Aus Experimenten wissen wir, dass die H-C-H- und H-C-C-Winkel in Ethen etwa 120° betragen. Dieser Winkel deutet darauf hin, dass die Kohlenstoffatome sp2-hybridisiert sind, was bedeutet, dass sich ein einfach besetztes sp2-Orbital auf einem Kohlenstoff mit einem einfach besetzten s-Orbital auf jedem H und einem einfach besetzten sp2-Lappen auf dem anderen C überlappt. (a) Das σ-gebundene Gerüst wird durch die Überlappung von zwei Gruppen einfach besetzter sp2-Hybridorbitale des Kohlenstoffs und vier einfach besetzten 1s-Orbitalen des Wasserstoffs gebildet, um Elektronenpaarbindungen zu bilden. Dabei werden 10 der 12 Valenzelektronen verwendet, um insgesamt fünf σ-Bindungen zu bilden (vier C-H-Bindungen und eine C-C-Bindung). (b) Ein einzeln besetztes unhybridisiertes 2pz-Orbital verbleibt an jedem Kohlenstoffatom, um eine Kohlenstoff-Kohlenstoff-π-Bindung zu bilden. (Anmerkung: Bei planaren Molekülen ist die Achse senkrecht zur Molekülebene die z-Achse.)
Die Hückel-Approximation wird zur Bestimmung der Energien und Formen der \pi-Molekülorbitale in konjugierten Systemen verwendet. Im Rahmen der Hückel-Approximation kann die kovalente Bindung in diesen Kohlenwasserstoffen in zwei unabhängige „Rahmen“ aufgeteilt werden: den \sigma -bindenden Rahmen und den \sigma -bindenden Rahmen. Die Wellenfunktionen, die zur Beschreibung der Bindungsorbitale in jedem Rahmen verwendet werden, ergeben sich aus unterschiedlichen Kombinationen von Atomorbitalen. Die Methode beschränkt sich auf konjugierte Kohlenwasserstoffe, und es werden nur \pi-Elektronen-Molekülorbitale berücksichtigt, da diese die allgemeinen Eigenschaften dieser Moleküle bestimmen; die Sigma-Elektronen werden ignoriert. Dies wird als Sigma-Pi-Trennbarkeit bezeichnet und ist durch die Orthogonalität von \sigma- und \pi-Orbitalen in planaren Molekülen begründet. Aus diesem Grund ist die Hückel-Methode auf planare Systeme beschränkt. Die Hückel-Approximation geht davon aus, dass die Elektronen in den \pi-Bindungen ein elektrostatisches Potenzial aufgrund des gesamten \sigma -Bindungsgerüsts im Molekül „spüren“ (d. h. sie konzentriert sich nur auf die Bildung von \pi-Bindungen, da das \sigma -Bindungsgerüst bereits gebildet wurde).
Konjugierte Systeme
Ein konjugiertes System hat einen Bereich von überlappenden p-Orbitalen, die die dazwischenliegenden Einfachbindungen überbrücken und eine Delokalisierung von \pi-Elektronen über alle benachbarten ausgerichteten p-Orbitale hinweg ermöglichen. Diese \pi-Elektronen gehören nicht zu einer einzelnen Bindung oder einem einzelnen Atom, sondern zu einer Gruppe von Atomen.
Ethen
Bevor wir die Hückel-Behandlung für Ethen betrachten, ist es nützlich, das allgemeine Bindungsbild des Moleküls zu überprüfen. Die Bindung in Ethen beinhaltet die sp^2-Hybridisierung der 2s , 2p_x und 2p_y Atomorbitale an jedem Kohlenstoffatom; die 2p_z Orbitale bleiben unberührt (Abbildung 13.2).
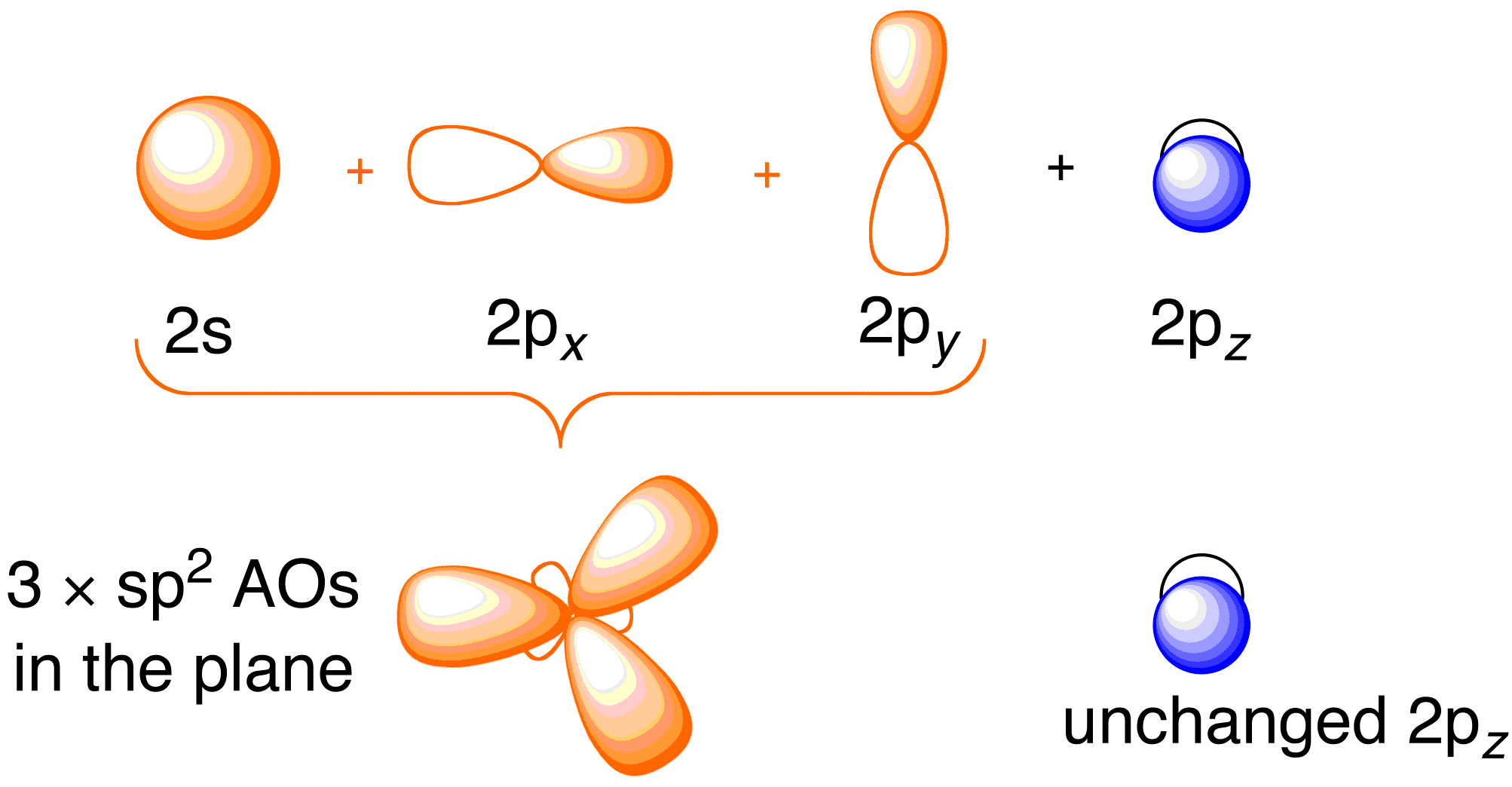
Abbildung 13.2. Hybridisierung der Kohlenstoff-Atomorbitale zu sp^2-Hybridorbitalen für die Bindung an Wasserstoffatome in Ethen. Bild mit Genehmigung von ChemTube (CC-SA-BY-NC; Nick Greeves).
Die Verwendung von Hybridorbitalen im hier beschriebenen Molekülorbitalansatz ist lediglich eine Bequemlichkeit und kein (direkter) Rückgriff auf die Valenzbindungstheorie. Eine identische Beschreibung kann durch die ausschließliche Verwendung von Atomorbitalen auf Kohlenstoff gewonnen werden, aber die Interpretation der resultierenden Wellenfunktionen ist weniger intuitiv. Zum Beispiel kann das i-te Molekülorbital durch Hybridorbitale
\
oder durch Atomorbitale beschrieben werden.
\
wobei \{a_i\} und \{c_i\} Koeffizienten der Expansion sind. Beide Beschreibungen funktionieren, und beide sind identische Ansätze, da
\
wobei \{c_i\} Koeffizienten sind, die das hybridisierte Orbital beschreiben.
Die Bindung erfolgt über die Vermischung der Elektronen in den sp^2-Hybridorbitalen des Kohlenstoffs mit den Elektronen in den 1s-Atomorbitalen der vier Wasserstoffatome (Abbildung 13.2. oben links), wodurch das \sigma -Bindungsgerüst entsteht. Das \pi -Bindungsgerüst ergibt sich aus den unhybridisierten 2p_z-Orbitalen (Abbildung 13.2. oben rechts). Die Unabhängigkeit dieser beiden Systeme wird in dem sich daraus ergebenden Molekülorbitaldiagramm in der nachstehenden Abbildung deutlich; die Hückel-Theorie befasst sich nur mit der Beschreibung der Molekülorbitale und Energien des \pi-Bindungssystems.

Abbildung 13.3: Molekülorbitale, die die Sigma-Pi-Trennbarkeit des \pi -Bindungsgerüsts (blau) und des \sigma -Bindungsgerüsts (rot) von Ethylen zeigen.
Die Hückel-Behandlung befasst sich nur mit der Beschreibung der Molekülorbitale und Energien des \pi-Bindungsgerüsts.
Da die Hückel-Theorie eine spezielle Betrachtung der Molekülorbitaltheorie ist, können die Molekülorbitale | \psi_i \rangle als Linearkombination der 2p_z-Atomorbitale \phi am Kohlenstoff mit ihren entsprechenden \{c_i\}-Koeffizienten beschrieben werden:
\
Die vollständige quantenchemische Analyse unter Verwendung der Schrödinger-Gleichung (nicht erforderlich für den Unterricht in organischer Chemie) finden Sie auf dieser Libretextseite.
Diese Molekülorbitale bilden das π-Bindungsgerüst, und da jeder Kohlenstoff ein Elektron zu diesem Gerüst beiträgt, ist im Grundzustand nur das niedrigste Molekülorbital ( | \psi_1 \rangle ) besetzt (Abbildung ). Die entsprechende Elektronenkonfiguration ist dann \pi_1^2 .

Abbildung 13.4: Schematische Darstellung des \pi-Molekülorbitalsystems für Ethylen . Man beachte, dass das antibindende Molekülorbital erwartungsgemäß einen Knoten mehr hat als das bindende Molekülorbital, da es eine höhere Energie aufweist.
HOMO und LUMO sind Akronyme für das höchste besetzte Molekülorbital bzw. das niedrigste unbesetzte Molekülorbital und werden oft auch als Grenzorbitale bezeichnet. Der Energieunterschied zwischen dem HOMO und dem LUMO wird als HOMO-LUMO-Lücke bezeichnet.
Die 3D-berechneten \pi-Molekülorbitale sind in Abbildung 13.5 dargestellt.

Abbildung 13.5: Berechnete \pi-Molekülorbitale für Ethylen . (links) das bindende Orbital (ψ1) und (rechts) das antibindende Orbital (ψ2).
Beitragende
- Seymour Blinder (emeritierter Professor für Chemie und Physik an der Universität von Michigan, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
