Ein Dreieck mit einem rechten Winkel nennt man rechtwinkliges Dreieck. Die Seite, die dem rechten Winkel gegenüberliegt, nennt man Hypotenuse des Dreiecks. Die beiden anderen Seiten nennt man Schenkel. Die beiden anderen Winkel haben keinen besonderen Namen, aber sie sind immer komplementär. Verstehst du, warum? Die Gesamtsumme der Winkel eines Dreiecks ist 180 Grad, und der rechte Winkel ist 90 Grad, also müssen die anderen beiden 90 Grad ergeben.
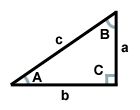
Das obige Dreieck hat die Seite c als Hypotenuse, die Seiten a und b als Schenkel und den Winkel C als rechten Winkel. Die Winkel A und B sind komplementär.
Es gibt zwei Arten von rechtwinkligen Dreiecken, die jeder Mathematiker sehr gut kennen sollte. Das eine ist das rechtwinklige Dreieck, das entsteht, wenn man von einer Spitze eines gleichseitigen Dreiecks eine Höhe abzieht und so zwei kongruente rechtwinklige Dreiecke bildet. Die Winkel des Dreiecks betragen 30, 60 und 90 Grad, was dem Dreieck seinen Namen gibt: 30-60-90-Dreieck. Das Verhältnis der Seitenlängen in solchen Dreiecken ist immer gleich: Wenn der Schenkel gegenüber dem 30-Grad-Winkel die Länge x hat, hat der Schenkel gegenüber dem 60-Grad-Winkel die Länge x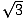
, und die Hypotenuse gegenüber dem rechten Winkel ist 2x. Hier ist ein 30-60-90-Dreieck abgebildet.
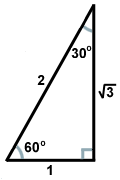
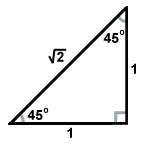
Das andere häufige rechtwinklige Dreieck ergibt sich aus dem Dreieckspaar, das entsteht, wenn eine Diagonale ein Quadrat in zwei Dreiecke teilt. Jedes dieser Dreiecke ist kongruent und hat die Winkelmaße 45, 45 und 90 Grad. Wenn die Schenkel, die den 45-Grad-Winkeln gegenüberliegen, die Länge x haben, hat die Hypotenuse eine Länge von x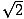
. Dieses Verhältnis gilt für alle 45-45-90-Dreiecke. 45-45-90-Dreiecke werden oft auch gleichschenklige rechtwinklige Dreiecke genannt.
Ein letztes Merkmal, das zu beachten ist, ist, dass die Schenkel eines rechtwinkligen Dreiecks auch Höhen des Dreiecks sind. Daher ist der Flächeninhalt eines rechtwinkligen Dreiecks die Hälfte des Produkts der Schenkellängen.