Bei einer Normalverteilung sind die Daten symmetrisch und nicht schief verteilt. In einem Diagramm folgen die Daten einer Glockenform, wobei sich die meisten Werte um einen zentralen Bereich gruppieren und sich mit zunehmender Entfernung vom Zentrum verjüngen.
Normalverteilungen werden wegen ihrer Form auch Gaußverteilungen oder Glockenkurven genannt.

- Warum sind Normalverteilungen wichtig?
- Welche Eigenschaften haben Normalverteilungen?
- Wie hoch ist Ihre Plagiatsquote?
- Empirische Regel
- Zentraler Grenzwertsatz
- Formel der Normalkurve
- Was ist die Standardnormalverteilung?
- Wahrscheinlichkeitsermittlung mithilfe der z-Verteilung
- Häufig gestellte Fragen zu Normalverteilungen
Warum sind Normalverteilungen wichtig?
Alle Arten von Variablen in den Natur- und Sozialwissenschaften sind normal oder annähernd normal verteilt. Größe, Geburtsgewicht, Lesefähigkeit, Arbeitszufriedenheit oder SAT-Scores sind nur einige Beispiele für solche Variablen.
Weil normalverteilte Variablen so häufig sind, sind viele statistische Tests für normalverteilte Populationen konzipiert.
Wenn man die Eigenschaften von Normalverteilungen kennt, kann man mit Hilfe der Inferenzstatistik verschiedene Gruppen vergleichen und anhand von Stichproben Schätzungen über Populationen vornehmen.
Welche Eigenschaften haben Normalverteilungen?
Normalverteilungen haben wichtige Merkmale, die in Diagrammen leicht zu erkennen sind:
- Mittelwert, Median und Modus sind genau gleich.
- Die Verteilung ist symmetrisch um den Mittelwert – die Hälfte der Werte liegt unter dem Mittelwert und die Hälfte über dem Mittelwert.
- Die Verteilung kann durch zwei Werte beschrieben werden: den Mittelwert und die Standardabweichung.


Der Mittelwert ist der Lageparameter, während die Standardabweichung der Skalenparameter ist.
Der Mittelwert bestimmt, wo die Spitze der Kurve zentriert ist. Eine Erhöhung des Mittelwerts verschiebt die Kurve nach rechts, während eine Verringerung die Kurve nach links verschiebt.


Die Standardabweichung streckt oder quetscht die Kurve. Eine kleine Standardabweichung ergibt eine schmale Kurve, während eine große Standardabweichung zu einer breiten Kurve führt.


Empirische Regel
Die empirische Regel, oder die 68-95-99.7-Regel, sagt Ihnen, wo die meisten Ihrer Werte in einer Normalverteilung liegen:
- Rund 68% der Werte liegen innerhalb von 1 Standardabweichung vom Mittelwert.
- Rund 95% der Werte liegen innerhalb von 2 Standardabweichungen vom Mittelwert.
- Rund 99,7% der Werte liegen innerhalb von 3 Standardabweichungen vom Mittelwert.
Nach der empirischen Regel:
- Rund 68% der Ergebnisse liegen zwischen 1000 und 1300, 1 Standardabweichung über und unter dem Mittelwert.
- Rund 95% der Ergebnisse liegen zwischen 850 und 1450, 2 Standardabweichungen über und unter dem Mittelwert.
- Rund 99,7% der Ergebnisse liegen zwischen 700 und 1600, 3 Standardabweichungen über und unter dem Mittelwert.


Die empirische Regel ist eine schnelle Möglichkeit, sich einen Überblick über Ihre Daten zu verschaffen und nach Ausreißern oder Extremwerten zu suchen, die nicht diesem Muster folgen.
Wenn Daten aus kleinen Stichproben diesem Muster nicht genau folgen, dann sind andere Verteilungen wie die t-Verteilung möglicherweise besser geeignet. Sobald Sie die Verteilung Ihrer Variablen identifiziert haben, können Sie geeignete statistische Tests anwenden.
Zentraler Grenzwertsatz
Der zentrale Grenzwertsatz ist die Grundlage dafür, wie Normalverteilungen in der Statistik funktionieren.
In der Forschung sammelt man idealerweise Daten aus mehreren Zufallsstichproben innerhalb der Population, um eine gute Vorstellung von einem Populationsmittelwert zu erhalten. Eine Stichprobenverteilung des Mittelwertes ist die Verteilung der Mittelwerte dieser verschiedenen Stichproben.
Der zentrale Grenzwertsatz zeigt Folgendes:
- Gesetz der großen Zahlen: Wenn man den Stichprobenumfang (oder die Anzahl der Stichproben) erhöht, nähert sich der Stichprobenmittelwert dem Populationsmittelwert an.
- Bei mehreren großen Stichproben ist die Stichprobenverteilung des Mittelwerts normalverteilt, selbst wenn die ursprüngliche Variable nicht normalverteilt ist.
Parametrische statistische Tests gehen in der Regel davon aus, dass die Stichproben aus normalverteilten Populationen stammen, aber der zentrale Grenzwertsatz bedeutet, dass diese Annahme nicht erfüllt werden muss, wenn die Stichprobe groß genug ist.
Sie können parametrische Tests für große Stichproben aus Populationen mit beliebiger Verteilung verwenden, solange andere wichtige Annahmen erfüllt sind. Ein Stichprobenumfang von 30 oder mehr gilt im Allgemeinen als groß.
Für kleine Stichproben ist die Normalitätsannahme wichtig, weil die Stichprobenverteilung des Mittelwerts nicht bekannt ist. Um genaue Ergebnisse zu erzielen, muss man sicher sein, dass die Grundgesamtheit normalverteilt ist, bevor man parametrische Tests mit kleinen Stichproben verwenden kann.
Formel der Normalkurve
Wenn man den Mittelwert und die Standardabweichung einer Normalverteilung kennt, kann man eine Normalkurve an die Daten anpassen, indem man eine Wahrscheinlichkeitsdichtefunktion verwendet.


In einer Wahrscheinlichkeitsdichtefunktion gibt die Fläche unter der Kurve die Wahrscheinlichkeit an. Die Normalverteilung ist eine Wahrscheinlichkeitsverteilung, also ist die Gesamtfläche unter der Kurve immer 1 oder 100%.
Die Formel für die normale Wahrscheinlichkeitsdichtefunktion sieht ziemlich kompliziert aus. Aber um sie zu benutzen, muss man nur den Mittelwert und die Standardabweichung der Population kennen.
Für jeden Wert von x kann man den Mittelwert und die Standardabweichung in die Formel einsetzen, um die Wahrscheinlichkeitsdichte der Variablen zu finden, die diesen Wert von x annimmt.
| Normale Wahrscheinlichkeitsdichteformel | Erläuterung |
|---|---|
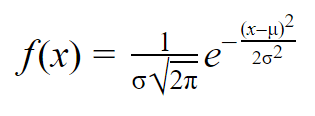 |
|
In Ihrem Diagramm der Wahrscheinlichkeitsdichtefunktion ist die Wahrscheinlichkeit die schattierte Fläche unter der Kurve, die rechts von dem Punkt liegt, an dem die SAT-Punkte 1380 betragen.


Den Wahrscheinlichkeitswert dieses Ergebnisses können Sie mit Hilfe der Standardnormalverteilung ermitteln.
Was ist die Standardnormalverteilung?
Die Standardnormalverteilung, auch z-Verteilung genannt, ist eine spezielle Normalverteilung, bei der der Mittelwert gleich 0 und die Standardabweichung gleich 1 ist.
Jede Normalverteilung ist eine Version der Standardnormalverteilung, die gestreckt oder gestaucht und horizontal nach rechts oder links verschoben wurde.


Während einzelne Beobachtungen aus Normalverteilungen mit x bezeichnet werden, werden sie in der z-Verteilung mit z bezeichnet. Jede Normalverteilung kann in die Standardnormalverteilung umgewandelt werden, indem die einzelnen Werte in z-Werte umgewandelt werden.
Z-Werte geben an, wie viele Standardabweichungen vom Mittelwert jeder Wert entfernt liegt.


Man muss nur den Mittelwert und die Standardabweichung der Verteilung kennen, um den z-Wert eines Wertes zu ermitteln.
| Z-Score Formel | Erläuterung |
|---|---|
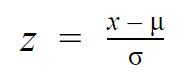 |
|
Aus mehreren Gründen wandeln wir Normalverteilungen in die Standardnormalverteilung um:
- Um die Wahrscheinlichkeit zu ermitteln, mit der Beobachtungen in einer Verteilung über oder unter einen bestimmten Wert fallen.
- Um die Wahrscheinlichkeit zu ermitteln, dass ein Stichprobenmittelwert signifikant von einem bekannten Populationsmittelwert abweicht.
- Um die Werte verschiedener Verteilungen mit unterschiedlichen Mittelwerten und Standardabweichungen zu vergleichen.
Wahrscheinlichkeitsermittlung mithilfe der z-Verteilung
Jeder z-Wert ist mit einer Wahrscheinlichkeit oder einem p-Wert verbunden, der angibt, wie wahrscheinlich es ist, dass Werte unterhalb dieses z-Wertes auftreten. Wenn Sie einen einzelnen Wert in einen z-Wert umwandeln, können Sie die Wahrscheinlichkeit des Auftretens aller Werte bis zu diesem Wert in einer Normalverteilung ermitteln.
Der Mittelwert unserer Verteilung ist 1150, und die Standardabweichung ist 150. Der z-Score gibt an, um wie viele Standardabweichungen 1380 vom Mittelwert entfernt ist.
| Formel | Berechnung |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
Für einen z-Score von 1,53 beträgt der p-Wert 0,937. Das ist die Wahrscheinlichkeit, dass der SAT-Score 1380 oder weniger beträgt (93,7 %), und es ist die Fläche unter der Kurve links von der schattierten Fläche.


Um die schattierte Fläche zu finden, muss man 0.937 von 1 ab, was die Gesamtfläche unter der Kurve ist.
Wahrscheinlichkeit von x>1380 = 1 – 0,937 = 0,063
Das bedeutet, dass wahrscheinlich nur 6,3 % der SAT-Punkte in Ihrer Stichprobe 1380 übersteigen.
Häufig gestellte Fragen zu Normalverteilungen
Bei einer Normalverteilung sind die Daten symmetrisch und nicht schief verteilt. Die meisten Werte gruppieren sich um einen zentralen Bereich, wobei sich die Werte mit zunehmender Entfernung vom Zentrum verjüngen.
Die Maße der zentralen Tendenz (Mittelwert, Modus und Median) sind in einer Normalverteilung genau gleich.
Die Standardnormalverteilung, auch z-Verteilung genannt, ist eine spezielle Normalverteilung, bei der der Mittelwert gleich 0 und die Standardabweichung gleich 1 ist.
Jede Normalverteilung kann in die Standardnormalverteilung umgewandelt werden, indem die einzelnen Werte in z-Werte umgewandelt werden. In einer z-Verteilung geben die z-Werte an, wie viele Standardabweichungen vom Mittelwert jeder Wert entfernt liegt.
Die empirische Regel oder die 68-95-99,7-Regel gibt an, wo die meisten Werte in einer Normalverteilung liegen:
- Rund 68 % der Werte liegen innerhalb einer Standardabweichung vom Mittelwert.
- Rund 95 % der Werte liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
- Rund 99,7 % der Werte liegen innerhalb von 3 Standardabweichungen vom Mittelwert.
Die empirische Regel ist eine schnelle Möglichkeit, sich einen Überblick über Ihre Daten zu verschaffen und nach Ausreißern oder Extremwerten zu suchen, die nicht diesem Muster folgen.
Die t-Verteilung beschreibt eine Reihe von Beobachtungen, bei denen die meisten Beobachtungen in der Nähe des Mittelwerts liegen und der Rest der Beobachtungen die Schwänze auf beiden Seiten bildet. Sie ist eine Art der Normalverteilung, die für kleinere Stichproben verwendet wird, bei denen die Varianz der Daten unbekannt ist.
Die t-Verteilung bildet eine Glockenkurve, wenn sie in einem Diagramm dargestellt wird. Sie kann mathematisch durch den Mittelwert und die Standardabweichung beschrieben werden.

