En una distribución normal, los datos se distribuyen simétricamente sin sesgo. Cuando se trazan en un gráfico, los datos siguen una forma de campana, con la mayoría de los valores agrupados alrededor de una región central y disminuyendo a medida que se alejan del centro.
Las distribuciones normales también se llaman distribuciones gaussianas o curvas de campana debido a su forma.

- ¿Por qué son importantes las distribuciones normales?
- ¿Cuáles son las propiedades de las distribuciones normales?
- ¿Cuál es tu puntuación de plagio?
- Regla empírica
- Teorema del límite central
- Fórmula de la curva normal
- ¿Qué es la distribución normal estándar?
- Encontrar la probabilidad utilizando la distribución z
- Preguntas frecuentes sobre distribuciones normales
¿Por qué son importantes las distribuciones normales?
Todo tipo de variables en las ciencias naturales y sociales se distribuyen de forma normal o aproximadamente normal. La altura, el peso al nacer, la capacidad de lectura, la satisfacción en el trabajo o las puntuaciones de la selectividad son sólo algunos ejemplos de tales variables.
Debido a que las variables con distribución normal son tan comunes, muchas pruebas estadísticas están diseñadas para poblaciones con distribución normal.
Entender las propiedades de las distribuciones normales significa que puedes utilizar la estadística inferencial para comparar diferentes grupos y hacer estimaciones sobre poblaciones utilizando muestras.
¿Cuáles son las propiedades de las distribuciones normales?
Las distribuciones normales tienen características clave que son fáciles de detectar en los gráficos:
- La media, la mediana y la moda son exactamente iguales.
- La distribución es simétrica respecto a la media-la mitad de los valores caen por debajo de la media y la otra mitad por encima de la media.
- La distribución puede describirse mediante dos valores: la media y la desviación estándar.


La media es el parámetro de localización mientras que la desviación estándar es el parámetro de escala.
La media determina dónde se centra el pico de la curva. El aumento de la media desplaza la curva hacia la derecha, mientras que su disminución la desplaza hacia la izquierda.


La desviación estándar estira o aprieta la curva. Una desviación estándar pequeña da lugar a una curva estrecha, mientras que una desviación estándar grande conduce a una curva ancha.


Regla empírica
La regla empírica, o la regla del 68-95-99.7 regla, le dice dónde se encuentra la mayoría de sus valores en una distribución normal:
- Alrededor del 68% de los valores están dentro de 1 desviación estándar de la media.
- Alrededor del 95% de los valores están dentro de 2 desviaciones estándar de la media.
- Alrededor del 99,7% de los valores están dentro de 3 desviaciones estándar de la media.
Siguiendo la regla empírica:
- Alrededor del 68% de las puntuaciones están entre 1000 y 1300, 1 desviación estándar por encima y por debajo de la media.
- Alrededor del 95% de las puntuaciones están entre 850 y 1450, 2 desviaciones estándar por encima y por debajo de la media.
- Alrededor del 99,7% de las puntuaciones están entre 700 y 1600, 3 desviaciones estándar por encima y por debajo de la media.


La regla empírica es una forma rápida de obtener una visión general de sus datos y comprobar si hay valores atípicos o extremos que no sigan este patrón.
Si los datos de muestras pequeñas no siguen de cerca este patrón, entonces otras distribuciones como la distribución t pueden ser más apropiadas. Una vez que identifique la distribución de su variable, puede aplicar las pruebas estadísticas apropiadas.
Teorema del límite central
El teorema del límite central es la base de cómo funcionan las distribuciones normales en estadística.
En la investigación, para obtener una buena idea de la media de una población, lo ideal es recoger datos de múltiples muestras aleatorias dentro de la población. Una distribución muestral de la media es la distribución de las medias de estas diferentes muestras.
El teorema del límite central muestra lo siguiente:
- Ley de los grandes números: A medida que aumenta el tamaño de la muestra (o el número de muestras), entonces la media de la muestra se acercará a la media de la población.
- Con múltiples muestras grandes, la distribución muestral de la media se distribuye normalmente, incluso si su variable original no se distribuye normalmente.
Las pruebas estadísticas paramétricas suelen suponer que las muestras proceden de poblaciones con distribución normal, pero el teorema del límite central significa que no es necesario cumplir este supuesto cuando se tiene una muestra suficientemente grande.
Se pueden utilizar pruebas paramétricas para muestras grandes de poblaciones con cualquier tipo de distribución siempre que se cumplan otros supuestos importantes. Un tamaño de muestra de 30 o más se considera generalmente grande.
Para las muestras pequeñas, el supuesto de normalidad es importante porque no se conoce la distribución muestral de la media. Para obtener resultados precisos, tiene que estar seguro de que la población está distribuida normalmente antes de poder utilizar pruebas paramétricas con muestras pequeñas.
Fórmula de la curva normal
Una vez que tenga la media y la desviación estándar de una distribución normal, puede ajustar una curva normal a sus datos utilizando una función de densidad de probabilidad.


En una función de densidad de probabilidad, el área bajo la curva te indica la probabilidad. La distribución normal es una distribución de probabilidad, por lo que el área total bajo la curva es siempre 1 o 100%.
La fórmula de la función de densidad de probabilidad normal parece bastante complicada. Pero para usarla, sólo necesitas conocer la media y la desviación estándar de la población.
Para cualquier valor de x, puedes introducir la media y la desviación estándar en la fórmula para encontrar la densidad de probabilidad de la variable que toma ese valor de x.
| Fórmula de la densidad de probabilidad normal | Explicación |
|---|---|
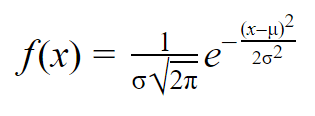 |
|
En su gráfico de la función de densidad de probabilidad, la probabilidad es el área sombreada bajo la curva que se encuentra a la derecha de donde las puntuaciones del SAT son iguales a 1380.


Puedes encontrar el valor de la probabilidad de esta puntuación utilizando la distribución normal estándar.
¿Qué es la distribución normal estándar?
La distribución normal estándar, también llamada distribución z, es una distribución normal especial en la que la media es 0 y la desviación estándar es 1.
Toda distribución normal es una versión de la distribución normal estándar que ha sido estirada o comprimida y desplazada horizontalmente hacia la derecha o hacia la izquierda.


Mientras que las observaciones individuales de las distribuciones normales se denominan x, se denominan z en la distribución z. Toda distribución normal puede convertirse en la distribución normal estándar convirtiendo los valores individuales en puntuaciones z.
Las puntuaciones z indican a cuántas desviaciones estándar de la media se encuentra cada valor.


Sólo necesitas conocer la media y la desviación estándar de tu distribución para encontrar la puntuación z de un valor.
| Fórmula de la puntuación Z | Explicación |
|---|---|
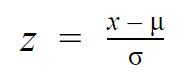 |
|
Convertimos las distribuciones normales en la distribución normal estándar por varias razones:
- Para encontrar la probabilidad de que las observaciones de una distribución caigan por encima o por debajo de un valor determinado.
- Para encontrar la probabilidad de que la media de una muestra difiera significativamente de una media poblacional conocida.
- Para comparar puntuaciones en diferentes distribuciones con diferentes medias y desviaciones estándar.
Encontrar la probabilidad utilizando la distribución z
Cada puntuación z está asociada con una probabilidad, o valor p, que le indica la probabilidad de que se produzcan valores por debajo de esa puntuación z. Si convierte un valor individual en una puntuación z, puede encontrar la probabilidad de que se produzcan todos los valores hasta ese valor en una distribución normal.
La media de nuestra distribución es 1150, y la desviación estándar es 150. La puntuación z te indica a cuántas desviaciones estándar se encuentra 1380 de la media.
| Fórmula | Cálculo |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
Para una puntuación z de 1,53, el valor p es 0,937. Esta es la probabilidad de que las puntuaciones de la selectividad sean de 1380 o menos (93,7%), y es el área bajo la curva a la izquierda del área sombreada.


Para encontrar el área sombreada, se resta 0.937 de 1, que es el área total bajo la curva.
Probabilidad de x>1380 = 1 – 0,937 = 0,063
Eso significa que es probable que sólo el 6,3% de las puntuaciones del SAT en su muestra superen 1380.
Preguntas frecuentes sobre distribuciones normales
En una distribución normal, los datos se distribuyen simétricamente sin sesgo. La mayoría de los valores se agrupan alrededor de una región central, y los valores disminuyen a medida que se alejan del centro.
Las medidas de tendencia central (media, moda y mediana) son exactamente las mismas en una distribución normal.
La distribución normal estándar, también llamada distribución z, es una distribución normal especial donde la media es 0 y la desviación estándar es 1.
Cualquier distribución normal puede convertirse en la distribución normal estándar convirtiendo los valores individuales en puntuaciones z. En una distribución z, las puntuaciones z indican a cuántas desviaciones estándar de la media se encuentra cada valor.
La regla empírica, o la regla del 68-95-99,7, te dice dónde se encuentra la mayoría de los valores en una distribución normal:
- Alrededor del 68% de los valores están dentro de 1 desviación estándar de la media.
- Alrededor del 95% de los valores están dentro de 2 desviaciones estándar de la media.
- Alrededor del 99,7% de los valores están dentro de 3 desviaciones estándar de la media.
La regla empírica es una forma rápida de obtener una visión general de sus datos y comprobar si hay valores atípicos o extremos que no siguen este patrón.
La distribución t es una forma de describir un conjunto de observaciones donde la mayoría de las observaciones caen cerca de la media, y el resto de las observaciones conforman las colas a ambos lados. Es un tipo de distribución normal que se utiliza para tamaños de muestra más pequeños, donde la varianza de los datos es desconocida.
La distribución t forma una curva de campana cuando se representa en un gráfico. Se puede describir matemáticamente utilizando la media y la desviación estándar.

