Logistisessa regressioanalyysissä lopputulos koodataan usein 0:ksi tai 1:ksi, jolloin 1 tarkoittaa, että kiinnostava lopputulos on olemassa, ja 0 tarkoittaa, että kiinnostava lopputulos puuttuu. Jos p määritellään todennäköisyydeksi, että lopputulos on 1, moninkertainen logistinen regressiomalli voidaan kirjoittaa seuraavasti:
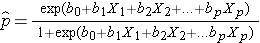
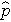on odotettu todennäköisyys sille, että lopputulos on läsnä; X1-Xp ovat erillisiä riippumattomia muuttujia; ja b0-bp ovat regressiokertoimet. Moninkertainen logistinen regressiomalli kirjoitetaan joskus toisin. Seuraavassa muodossa lopputulos on sen todennäköisyyden odotettu logaritmi, että lopputulos esiintyy,
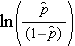
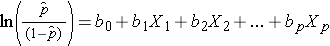
Huomaa, että yllä olevan yhtälön oikea puoli näyttää moninkertaisen lineaarisen regression yhtälöltä. Logistisen regressiomallin regressiokertoimien estimointitekniikka on kuitenkin erilainen kuin moninkertaisen lineaarisen regressiomallin regressiokertoimien estimointiin käytetty tekniikka. Logistisessa regressiossa mallista johdetut kertoimet (esim. b1) ilmaisevat odotetun log-kertoimen muutoksen suhteessa yhden yksikön muutokseen X1:ssä, kun kaikki muut ennustetekijät pidetään vakiona. Näin ollen estimoidun regressiokertoimen antilogi, exp(bi), tuottaa kertoimen suhdeluvun, kuten alla olevassa esimerkissä havainnollistetaan.
Esimerkki logistisesta regressiosta – lihavuuden ja sydän- ja verisuonitautien välinen yhteys
Analysoimme aiemmin tietoja tutkimuksesta, joka oli suunniteltu arvioimaan lihavuuden (määriteltynä BMI:llä > 30) ja sydän- ja verisuonitautien esiintymistapausten välistä yhteyttä. Tiedot kerättiin osallistujilta, jotka olivat 35-65-vuotiaita ja joilla ei ollut sydän- ja verisuonitautia (CVD) lähtötilanteessa. Kutakin osallistujaa seurattiin 10 vuoden ajan sydän- ja verisuonitautien kehittymisen varalta. Yhteenveto tiedoista on tämän moduulin sivulla 2. Korjaamaton tai karkea suhteellinen riski oli RR = 1,78 ja korjaamaton tai karkea odds ratio oli OR = 1,93. Määritimme myös, että ikä oli sekoittaja, ja Cochran-Mantel-Haenszel-menetelmää käyttäen arvioimme mukautetuksi suhteelliseksi riskiksi RRCMH =1,44 ja mukautetuksi kertoimeksi ORCMH =1,52. Seuraavaksi käytämme logistista regressioanalyysia arvioidaksemme liikalihavuuden ja sydän- ja verisuonitautitapahtuman välistä yhteyttä ikään sopeutettuna.
Logistinen regressioanalyysi paljastaa seuraavaa:
|
riippumaton muuttuja |
regressiokerroin |
Chi-ruutu |
P-arvo |
|---|---|---|---|
|
sisäpiste |
-2.367 |
307.38 |
0.0001 |
|
Obesiteetti |
0.658 |
9.87 |
0.0017 |
Yksinkertainen logistinen regressiomalli suhteuttaa liikalihavuuden esiintyvän CVD:n log-kertoimiin:
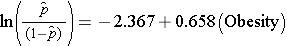
Ylipaino on mallissa indikaattorimuuttuja, joka koodataan seuraavasti: 1 = lihava ja 0 = ei lihava. Tapahtuneen CVD:n log-kertoimet ovat 0,658 kertaa suuremmat henkilöillä, jotka ovat lihavia kuin ei-lihavilla. Jos otamme regressiokertoimen antilog, exp(0,658) = 1,93, saamme karkean tai korjaamattoman kertoimen. Kertoimet sairastua sydän- ja verisuonitautiin ovat 1,93 kertaa suuremmat lihavilla henkilöillä kuin ei-lihavilla henkilöillä. Lihavuuden ja sydän- ja verisuonitautitapausten välinen yhteys on tilastollisesti merkitsevä (p=0,0017). Huomattakoon, että logistisen regressioanalyysin regressioparametrien merkitsevyyden arvioinnissa käytettävät testitilastot perustuvat khiin neliö -tilastoihin eikä t-tilastoihin, kuten lineaarisen regressioanalyysin tapauksessa. Tämä johtuu siitä, että regressioparametrien estimoinnissa käytetään erilaista estimointitekniikkaa, niin sanottua maksimaalisen todennäköisyyden estimointia (katso Hosmer ja Lemeshow3 teknisistä yksityiskohdista).
Monissa tilastollisissa laskentapaketeissa luodaan myös kertoimien suhdeluvut sekä 95 %:n luottamusvälit kertoimien suhdeluvuille osana logistista regressioanalyysia. Tässä esimerkissä odds ratio -estimaatti on 1,93 ja 95 %:n luottamusväli on (1,281, 2,913).
Tarkastellessamme liikalihavuuden ja CVD:n välistä yhteyttä määrittelimme aiemmin, että ikä oli sekoittaja.Seuraavassa moninkertaisessa logistisessa regressiomallissa arvioidaan liikalihavuuden ja esiintyvän CVD:n välistä yhteyttä, kun ikä otetaan huomioon. Mallissa otetaan jälleen huomioon kaksi ikäryhmää (alle 50-vuotiaat ja 50-vuotiaat ja sitä vanhemmat). Analyysissä ikäryhmä koodataan seuraavasti: 1=50-vuotiaita ja vanhempia ja 0= alle 50-vuotiaita.
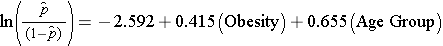
Jos otamme lihavuuteen liittyvän regressiokertoimen antilogin, exp(0.415) = 1.52, saamme iästä puhdistetun kertoimen. Kertoimet sairastua sydän- ja verisuonitautiin ovat 1,52 kertaa suuremmat liikalihavilla henkilöillä kuin ei-lihavilla henkilöillä, kun ikä otetaan huomioon. Kohdassa 9.2 käytimme Cochran-Mantel-Haenszel-menetelmää ikään sovitetun kertoimen tuottamiseksi ja saimme seuraavan tuloksen:
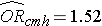
Tämä havainnollistaa, miten moninkertaista logistista regressioanalyysia voidaan käyttää sekoittavien tekijöiden huomioon ottamiseksi. Malleja voidaan laajentaa ottamaan huomioon useita sekoittavia muuttujia samanaikaisesti. Moninkertaista logistista regressioanalyysia voidaan käyttää myös sekoittumisen ja vaikutuksen muuttumisen arviointiin, ja lähestymistavat ovat samat kuin moninkertaisessa lineaarisessa regressioanalyysissä. Moninkertaista logistista regressioanalyysia voidaan käyttää myös useiden riskitekijöiden vaikutuksen tutkimiseen (sen sijaan, että keskityttäisiin yhteen riskitekijään) kaksinumeroisessa lopputuloksessa.
Esimerkki – Riskitekijät, jotka liittyvät matalaan syntymäpainoon
Esitettäköön, että tutkijat ovat huolissaan myös haitallisista raskausajan lopputuloksista, mukaan luettuina raskausdiabetes, pre-eklampsia (eli raskaudenaikainen verenpainetauti) ja ennenaikainen synnytys. Muistutetaan, että tutkimukseen osallistui 832 raskaana olevaa naista, jotka toimittivat demografisia ja kliinisiä tietoja. Tutkimusnäytteestä 22 (2,7 %) naiselle kehittyy pre-eklampsia, 35 (4,2 %) raskausdiabetes ja 40 (4,8 %) ennenaikainen synnytys. Oletetaan, että halutaan arvioida, onko näissä raskauden haittatapahtumissa eroja rodun/etnisen alkuperän mukaan, kun otetaan huomioon äidin ikä. Suoritettiin kolme erillistä logistista regressioanalyysiä, joissa kukin lopputulos yhdistettiin erikseen kolmeen dummy- tai indikaattorimuuttujaan, jotka kuvastavat äidin rotua ja äidin ikää (vuosina). Tulokset ovat seuraavat.
|
Tulos: Pre-eklampsia |
Regressiokerroin |
Chi-neliö |
P-arvo |
Odds Ratio (95 %:n CI) |
|---|---|---|---|---|
|
Intersektiokertoimen |
-3.066 |
4.518 |
0.0335 |
– |
|
Musta rotu |
2.191 |
12.640 |
0.0004 |
8.948 (2.673, 29.949) |
|
Hispanic race |
-0.1053 |
0.0325 |
0.8570 |
0.900 (0.286, 2.829) |
|
Muu rotu |
0.0586 |
0.0021 |
0.9046 |
1.060 (0.104, 3.698) |
|
Äitien ikä (v.) |
-0.0252 |
0.3574 |
0.5500 |
0.975 (0.898, 1.059) |
Ainut tilastollisesti merkitsevä ero pre-eklampsian esiintyvyydessä on mustien ja valkoihoisten äitien välillä.
Mustat äidit sairastuvat lähes yhdeksänkertaisella todennäköisyydellä preeklampsiaan valkoisiin äiteihin nähden, kun otetaan huomioon äidin ikä. Pre-eklampsian sairastavien mustien ja valkoisten äitien välisen kertoimen 95 prosentin luottamusväli on hyvin laaja (2,673 – 29,949). Tämä johtuu siitä, että lopputapahtumien määrä on pieni (vain 22 naiselle kehittyy pre-eklampsia koko otoksessa) ja että tutkimuksessa on vain pieni määrä mustaihoisia naisia. Näin ollen tätä yhteyttä on tulkittava varovaisesti.
Vaikka odds ratio on tilastollisesti merkitsevä, luottamusväli viittaa siihen, että vaikutuksen suuruus voisi olla 2,6-kertaisesta lisäyksestä 29,9-kertaiseen lisäykseen. Vaikutuksen tarkemman arvion saamiseksi tarvitaan suurempi tutkimus.
|
raskausdiabetes |
regressiokerroin |
Chi-neliö |
P-arvo |
Odds Ratio (95% CI) |
|---|---|---|---|---|
|
Intercept |
-5.823 |
22.968 |
0.0001 |
– |
|
Musta rotu |
1.621 |
6.660 |
0.0099 |
5.056 (1.477, 17.312) |
|
Hispanic race |
0.581 |
1.766 |
0.1839 |
1.787 (0.759, 4.207) |
|
Muu rotu |
1.348 |
5.917 |
0.0150 |
3.848 (1.299, 11.395) |
|
Äidin ikä (v.) |
0.071 |
4.314 |
0.0378 |
1.073 (1.004, 1.147) |
Raskausdiabeteksen osalta on tilastollisesti merkitseviä eroja mustien ja valkoihoisten äitien välillä (p=0.0099) sekä itseään muuksi roduksi identifioivien äitien välillä valkoihoisiin verrattuna (p=0.0150) äidin iän mukaan korjattuna. Äidin ikä on myös tilastollisesti merkitsevä (p=0,0378), ja vanhemmilla naisilla on suurempi todennäköisyys sairastua raskausdiabetekseen, korjattuna rodun/etnisyyden mukaan.
|
Tulos: Ennenaikainen synnytys |
Regressiokerroin |
Chi-neliö |
P-arvo |
Odds Ratio (95 %:n CI) |
|---|---|---|---|---|
|
Interepti |
-1.443 |
1.602 |
0.2056 |
– |
|
Musta rotu |
-0.082 |
0.015 |
0.9039 |
0.921 (0.244, 3.483) |
|
Hispanic race |
-1.564 |
9.497 |
0.0021 |
0.209 (0.077, 0.566) |
|
Muu rotu |
0.548 |
1.124 |
0.2890 |
1.730 (0.628,4.767) |
|
Äidin ikä (v. Latinalaisamerikkalaisilla äideillä on 80 % pienempi todennäköisyys sairastua ennenaikaiseen synnytykseen kuin valkoisilla äideillä (odds ratio = 0,209), äidin iän mukaan oikaistuna. Multimuuttujamenetelmät ovat laskennallisesti monimutkaisia ja edellyttävät yleensä tilastollisen laskentapaketin käyttöä. Monimuuttujamenetelmiä voidaan käyttää sekoittavien tekijöiden On tärkeää muistaa, että monimuuttujamalleilla voidaan säätää tai ottaa huomioon vain tutkimuksessa mitattujen sekoittavien muuttujien erot. Lisäksi monimuuttujamalleja tulisi käyttää sekoittavien tekijöiden huomioon ottamiseen vain silloin, kun sekoittavien tekijöiden jakaumissa on jonkin verran päällekkäisyyttä kussakin riskitekijäryhmässä. Stratifioidut analyysit ovat hyvin informatiivisia, mutta jos otokset tietyissä ositteissa ovat liian pieniä, analyyseistä voi puuttua tarkkuutta. Tutkimuksia suunnitellessaan tutkijoiden on kiinnitettävä huolellisesti huomiota mahdollisiin vaikutuksen muokkaajiin. Jos epäillään, että altistumisen tai riskitekijän välinen yhteys on erilainen tietyissä ryhmissä, tutkimus on suunniteltava siten, että varmistetaan riittävä määrä osallistujia kussakin näistä ryhmistä. Otoskokokaavojen avulla on määritettävä, kuinka monta tutkittavaa tarvitaan kussakin ositteessa, jotta analyysin riittävä tarkkuus tai teho voidaan varmistaa. palaa alkuun | edellinen sivu | seuraava sivu |