Normaalijakaumassa data on symmetrisesti jakautunutta ilman vinoutta. Kun tiedot piirretään kuvaajaan, ne noudattavat kellon muotoa, jossa useimmat arvot ryhmittyvät keskialueen ympärille ja kapenevat kauemmas keskustasta mentäessä.
Normaalijakaumia kutsutaan niiden muodon vuoksi myös Gaussin jakaumiksi tai kellokäyriksi.

Miksi normaalijakaumilla on väliä?
Kaikenlaiset luonnon- ja yhteiskuntatieteellisissä aineistoissa esiintyvät muuttujat ovat normaalisti tai likimääräisesti normaalisti jakautuneita. Pituus, syntymäpaino, lukutaito, työtyytyväisyys tai SAT-pisteet ovat vain muutamia esimerkkejä tällaisista muuttujista.
Koska normaalijakautuneet muuttujat ovat niin yleisiä, monet tilastolliset testit on suunniteltu normaalijakautuneita populaatioita varten.
Normaalijakaumien ominaisuuksien ymmärtäminen tarkoittaa, että voit käyttää päättelytilastoja vertaillaksesi eri ryhmiä ja tehdessäsi otosten avulla estimaatteja populaatioista.
Mitä ominaisuuksia normaalijakaumilla on?
Normaalijakaumilla on keskeisiä ominaisuuksia, jotka on helppo havaita kuvaajista:
- Keskiarvo (mean), mediaani (mediaani) ja moodi (moodi) ovat täsmälleen samanlaisia.
- Jakauma on symmetrinen keskiarvon suhteen – puolet arvoista jää keskiarvon alapuolelle ja puolet keskiarvon yläpuolelle.
- Jakaumaa voidaan kuvata kahdella arvolla: keskiarvolla ja keskihajonnalla.


Keskiarvo on paikannusparametri, kun taas keskihajonta on asteikkoparametri.
Keskiarvo määrittää, missä käyrän huipun keskipiste sijaitsee. Keskiarvon kasvattaminen siirtää käyrää oikealle ja sen pienentäminen vasemmalle.


Keskihajonta venyttää tai puristaa käyrää. Pieni keskihajonta johtaa kapeaan käyrään, kun taas suuri keskihajonta johtaa leveään käyrään.


Empiirinen sääntö
Empiirisen säännön, tai 68-95-99.7-sääntö, kertoo, mihin suurin osa arvoista sijoittuu normaalijakaumassa:
- Noin 68 % arvoista on 1 keskihajonnan sisällä keskiarvosta.
- Noin 95 % arvoista on 2 keskihajonnan sisällä keskiarvosta.
- Noin 99,7 % arvoista on 3 keskihajonnan sisällä keskiarvosta.
Empiirisen säännön noudattaminen:
- Ympäri 68 % pisteistä on välillä 1000-1300, 1 keskihajonta keskiarvon ylä- ja alapuolella.
- Ympäri 95 % pisteistä on välillä 850-1450, 2 keskihajontaa keskiarvon ylä- ja alapuolella.
- Ympäri 99,7 % pisteistä on välillä 700-1600, 3 keskihajontaa keskiarvon ylä- ja alapuolella.


Empiirinen sääntö on nopea tapa saada yleiskuva tiedoistasi ja tarkastaa, onko aineistossasi poikkeavia tai ääriarvoja, jotka eivät noudata tätä kaavaa.
Jos pienistä otannoista saadut tiedot eivät noudata tarkkaan kyseistä kaavaa, muut jakaumat, kuten t-jakautuma, voivat olla sopivampia. Kun olet tunnistanut muuttujasi jakauman, voit soveltaa sopivia tilastollisia testejä.
Keskiarvoteoreema
Keskiarvoteoreema on perusta sille, miten normaalijakaumat toimivat tilastotieteessä.
Tutkimuksessa saadaksesi hyvän käsityksen populaatiokeskiarvosta ideaalitapauksessa keräät tietoja useista satunnaisotannoista populaation sisällä. Keskiarvon otantajakauma on näiden eri otosten keskiarvojen jakauma.
Keskiarvoteorema osoittaa seuraavaa:
- Suurten lukujen laki: Kun otoskoko (tai otosten lukumäärä) kasvaa, niin otoskeskiarvo lähestyy populaatiokeskiarvoa.
- Monella suurella otoksella keskiarvon otosjakauma on normaalijakautunut, vaikka alkuperäinen muuttuja ei olisikaan normaalijakautunut.
Parametriset tilastolliset testit yleensä olettavat, että otokset ovat peräisin normaalisti jakautuneista populaatioista, mutta keskusrajateorema tarkoittaa, että tätä oletusta ei tarvitse täyttää, kun sinulla on tarpeeksi suuri otos.
Voit käyttää parametrisia testejä suurille otoksille populaatioista, joilla on minkälainen jakauma tahansa, kunhan muut tärkeät oletukset täyttyvät. Otoskoko 30 tai enemmän katsotaan yleensä suureksi.
Pienten otosten kohdalla normaalisuusoletus on tärkeä, koska keskiarvon otantajakaumaa ei tunneta. Tarkkojen tulosten saamiseksi sinun on oltava varma, että perusjoukko on normaalijakautunut, ennen kuin voit käyttää parametrisia testejä pienillä otoksilla.
Normaalikäyrän kaava
Kun sinulla on normaalijakauman keskiarvo ja keskihajonta, voit sovittaa normaalikäyrän aineistoosi todennäköisyystiheysfunktion avulla.


Todennäköisyystiheysfunktiossa käyrän alle jäävä pinta-ala kertoo todennäköisyyden. Normaalijakauma on todennäköisyysjakauma, joten käyrän alle jäävä kokonaispinta-ala on aina 1 eli 100 %.
Normaalin todennäköisyystiheysfunktion kaava näyttää melko monimutkaiselta. Mutta sen käyttämiseksi sinun tarvitsee tietää vain populaation keskiarvo ja keskihajonta.
Minkä tahansa x:n arvon osalta voit liittää kaavan keskiarvon ja keskihajonnan kaavaan löytääksesi muuttujan todennäköisyystiheyden, joka ottaa kyseisen x:n arvon.
| Normaalin todennäköisyystiheyden kaava | selitys |
|---|---|
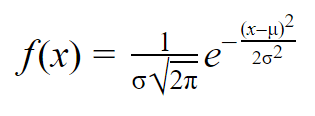 |
|
Todennäköisyystiheysfunktion kuvaajassasi todennäköisyys on se tummennettu käyrän alapuolinen alue, joka sijaitsee oikealla siitä kohdasta, jossa SAT-pisteet ovat yhtä suuret kuin 1380.


Voit löytää tämän pistemäärän todennäköisyysarvon käyttämällä vakionormaalijakaumaa.
Mikä on vakionormaalijakauma?
Standardinormaalijakauma, jota kutsutaan myös z-jakaumaksi, on erityinen normaalijakauma, jossa keskiarvo on 0 ja keskihajonta 1.
Jokainen normaalijakauma on versio standardinormaalijakaumasta, jota on venytetty tai puristettu ja siirretty vaakasuunnassa oikealle tai vasemmalle.


Mikäli yksittäisiä havaintoja normaalijakaumasta kutsutaan x:ksi, z-jakaumassa niitä kutsutaan z:ksi. Jokainen normaalijakauma voidaan muuntaa standardinormaalijakaumaksi muuttamalla yksittäiset arvot z-pistemääriksi.
Z-pistemäärät kertovat, kuinka monen keskihajonnan päässä keskiarvosta kukin arvo sijaitsee.


Tarvitaan vain jakauman keskiarvo ja keskihajonta, jotta arvon z-pistemäärä voidaan määrittää.
| Z-pistemäärän kaava | selitys |
|---|---|
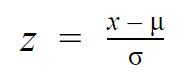 |
|
Muunnamme normaalijakaumat vakionormaalijakaumaksi useista syistä:
- Tutustuaksemme todennäköisyyteen, jolla jakauman havainnot jäävät tietyn arvon ylä- tai alapuolelle.
- Tutustuaksemme todennäköisyyteen, että otoskeskiarvo poikkeaa merkittävästi tunnetusta populaatiokeskiarvosta.
- Vertaillaksemme tuloksia eri jakaumilla, joilla on erilaiset keskiarvot ja keskihajonnat.
Todennäköisyyksien löytäminen z-jakauman avulla
Jokaiseen z-arvoon liittyy todennäköisyys eli p-arvo, joka kertoo, kuinka todennäköistä on, että kyseistä z-arvoa pienempiä arvoja esiintyy. Jos muunnat yksittäisen arvon z-arvoksi, voit sen jälkeen löytää kaikkien arvojen esiintymistodennäköisyyden kyseiseen arvoon asti normaalijakaumassa.
Jakaumamme keskiarvo on 1150, ja keskihajonta on 150. z-pistemäärä kertoo, kuinka monen keskihajonnan päässä 1380 on keskiarvosta.
| KAAVA | Laskelma |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
Jos z-arvo on 1,53, p-arvo on 0,937. Tämä on todennäköisyys sille, että SAT-pistemäärä on 1380 tai pienempi (93,7 %), ja se on tummennetun alueen vasemmalla puolella oleva käyrän alapuolinen alue.


Tummennetun alueen löytämiseksi otetaan pois 0.937 arvosta 1, joka on käyrän alle jäävä kokonaispinta-ala.
Todennäköisyys x>1380 = 1 – 0,937 = 0,063
Tämä tarkoittaa, että on todennäköistä, että vain 6,3 % otoksesi SAT-pistemääristä ylittää arvon 1380.
Tiheästi kysyttyjä kysymyksiä normaalijakaumiin liittyen
Normaalijakaumassa data on symmetrisesti jakautunutta ilman vinoutta. Useimmat arvot ryhmittyvät keskialueen ympärille, ja arvot kapenevat siirryttäessä kauemmas keskipisteestä.
Keskisuuntauksen mittarit (keskiarvo, moodi ja mediaani) ovat täsmälleen samat normaalijakaumassa.
Standardinormaalijakauma, jota kutsutaan myös z-jakaumaksi, on erityinen normaalijakauma, jossa keskiarvo on 0 ja keskihajonta on 1.
Mikä tahansa normaalijakauma voidaan muuntaa standardinormaalijakaumaksi muuttamalla yksittäiset arvot z-arvoiksi. z-jakaumassa z-pisteet kertovat, kuinka monen keskihajonnan päässä keskiarvosta kukin arvo sijaitsee.
Empiirinen sääntö eli 68-95-99,7-sääntö kertoo, missä suurin osa arvoista sijaitsee normaalijakaumassa:
- Ympäri 68 % arvoista on yhden keskihajonnan sisällä keskiarvosta.
- Yli 95 % arvoista on kahden keskihajonnan sisällä keskiarvosta.
- Ympäri 99,7 % arvoista on 3 keskihajonnan sisällä keskiarvosta.
Empiirinen sääntö on nopea tapa saada yleiskuva aineistostasi ja tarkistaa mahdolliset poikkeamat tai ääriarvot, jotka eivät noudata tätä kaavaa.
T-jakauma on tapa kuvata havaintojoukkoa, jossa suurin osa havainnoista osuu lähelle keskiarvoa ja loput havainnoista muodostavat hännät molemmin puolin. Se on eräänlainen normaalijakauma, jota käytetään pienempien otoskokojen tapauksessa, kun aineiston varianssi on tuntematon.
T-jakauma muodostaa kellokäyrän, kun se piirretään kuvaajaan. Sitä voidaan kuvata matemaattisesti keskiarvon ja keskihajonnan avulla.

