Opettaa lukuarvoja? How NOT to do it the Wrong Way!

Find out how to teach place value developmentally and appropriate to the grade with lesson ideas and a FREE Place Value Game!

I can still see Mrs. Pink lukion matematiikanopettajani (olin hänen apulaisopettajansa) selittämässä 1. jakson luokalleen, miksi heidän kannattaisi oppia kirjoittamaan shekki oikein (tämä oli 70-luvulla, joten kaikkien piti oppia kirjoittamaan shekki!). Haluatko todella laittaa desimaalipisteen mihin tahansa? Paikka-arvon ymmärtämättömyydellä voi olla vakavia taloudellisia seurauksia!

Mutta jos paikka-arvon ymmärtäminen tarkoittaa sitä, että numeron arvo tulkitaan oikein sen perusteella, mikä on sen paikka luvussa, pelkkä paikka-arvotaulukon käyttäminen ei luultavasti riitä!

Paikka-arvon opettaminen sisältää paljon liikkuvia osia. Oppilailla on oltava tietyt muut käsitteet hallussaan, ennen kuin he voivat aidosti sisäistää numeroiden arvon.

Paikka-arvon opettaminen on olennaista, koska se on viimeinen kivijalka alakoululaisten numerotajun rakentamisessa. Tässä postauksessa selitän, miten paikka-arvo kehittyy luokka-asteiden aikana. Näytän myös, miksi paikka-arvon opettaminen on opittava konkreettisesti eikä abstraktisti, jotta oppilaillesi kehittyy vankka käsitteellinen ymmärrys eikä pintapuolinen tieto paikka-arvosta.

Pohditko, miten paikka-arvoa voi opettaa etäopetusmallissa? Lue lisää siitä, miten opettaa paikka-arvoja virtuaalisesti verkossa.

Kokonaiskuvan eteneminen paikka-arvojen opettamisessa

Jos opetat matematiikan yhteisten perussuuntaviivojen (Common Core State Standards for Mathematics) mukaisesti, tiedät, että standardit ovat yhtenäisiä. Yhtä standardia kehitetään syvällisesti useilla luokkatasoilla. Paikka-arvo on yksi näistä standardeista.

Alkaen päiväkodista oppilaat oppivat, että teini-ikäiset luvut (11-29) muodostuvat luvuista 10 + x. 18 voidaan siis nähdä 10:nä ja 8:na (siksi on olennaista osata muodostaa 10!) Ensimmäisellä luokalla oppilaat jatkavat tätä oppiessaan lukuja aina 120:een asti. He oppivat, että kymmenet ja ykköset muodostavat kaksinumeroiset luvut. He oppivat niputtamaan 10 ykköstä kympiksi. Nämä kaikki standardit luovat olennaisen perustan paikka-arvolle: vasemmalla oleva luku on kymmenen kertaa enemmän kuin oikealla oleva luku tai päinvastoin, oikealla olevat luvut ovat kymmenesosan verran enemmän kuin vasemmalla olevat luvut.

Paikka-arvosta tulee todellista!

Kakkosluokalla paikka-arvojen opettaminen luvuille aina tuhanteen saakka nousee nyt ensiarvoisen tärkeäksi. Oppilaat eivät saa lähteä toiselta luokalta ymmärtämättä numeroiden arvoa yksikköinä, kymmeninä ja satasina. He eivät käytä paikka-arvoa ainoastaan moninumeroisten lukujen tunnistamiseen, vaan myös yhteen- ja vähennyslaskuihin ja lopulta kerto- ja jakolaskuihin.

Kolmannella luokalla oppilaat saattavat tarvita paikka-arvon kertausta, mutta heillä pitäisi olla vankka käsitys paikka-arvosta aina tuhanteen asti. Kolmannella luokalla murtoluvut esitellään vakiomuotoisina lukuina. Kokonaislukujen ja -arvojen tunteminen on välttämätöntä kokonaislukujen väliin jäävien murtolukujen ymmärtämiseksi.

Neljännellä ja viidennellä luokalla paikka-arvot menevät toiseen suuntaan: kymmenlukuihin. Kyllä, kokonaislukujen paikka-arvoa laajennetaan satatuhanteen, mutta myös kymmenlukujen osalta tuhannesosiin. Viidennen luokan loppuun mennessä useimmilla oppilailla pitäisi olla kunnollinen, ellei peräti vankka käsitteellinen ymmärrys kokonaislukujen, murtolukujen ja desimaalilukujen paikka-arvosta.

LUE LOPPUUN LOPPUUN LÖYTYÄKSESI, ETTÄ SAAT ILMAISEKSI PAIKKA-ARVOPELIN!

Manipulatiivit paikka-arvojen opettamiseen

Opiskelijoiden on nähtävä paikka-arvot konkreettisesti eikä abstraktisti paikka-arvotulosten taulukosta löytyvillä numeroin. On siis tärkeää, mitä manipulatiiveja käytät. Kun opetat paikka-arvoa, voit luokitella manipulatiivit ryhmiteltäviin tai esiryhmiteltyihin.

Place Value Manipulatives

.

Groupable Manipulatives	Pre-Ryhmitettävät manipulatiivit
unifix- tai linkkikuutiot	tikkuun liimatut pavut
paperiklipsejä	paikka-arvokiekkoja tai -lastuja
varret	perus 10 palikat
laskurit	Legot®

Kriittisen tärkeää on aloittaa ensin ryhmiteltävistä manipulatiiveista. Anna oppilaiden käydä läpi kymmenen tai sadan hengen ryhmien niputtaminen ja purkaminen. Useimmat lastentarhan ja ensimmäisen luokan opettajat käyttävät perus 10-palikoita paikka-arvojen opettamiseen. Ne eivät kuitenkaan ole sopivia näillä luokka-asteilla, koska 10-kantaisia palikoita ei voi irrottaa ryhmistä. Kyllä, niitä voidaan vaihtaa, mutta se ei ole sama asia.

Niputtaminen ja vaihtaminen paikka-arvossa

Lastentarhassa ja ensimmäisellä luokalla on tärkeää, että oppilaat niputtavat. Riippumatta siitä, niputtavatko he niputtamalla kuminauhan oljenkorsien ympärille, yhdistämällä Unifix-kuutioita tai ryhmittelemällä esineitä kuppiin, niputtaminen rakentaa käsitteellistä ymmärrystä 10 kertaa enemmän. Se opettaa oppilaita myös yksiköimään. Kun he laskevat ryhmän, se lasketaan 10:llä. Ryhmitettävien manipulatiivien käyttäminen näillä luokkatasoilla on siis tärkeää. Kun oppilaat ymmärtävät niputtamisen, aletaan siirtyä 10-kantaisiin palikoihin.

Kakkosluokalla ja siitä ylöspäin 10-kantaiset palikat ovat sopivampia, koska oppilaat ovat kehittäneet käsitteellisen ymmärryksensä paikka-arvosta, joka on 10 kertaa enemmän, ja siitä, että yksi kymppinippu on YKSI KYMPPI. Toisen luokan oppilaat alkavat niputtaa kymppiryhmiä 100:ksi. Toisen luokan oppilaat tarvitsevat paljon harjoitusta näiden kymppien niputtamiseen sadoiksi. Perus 10:n palikat sopivat tähän.

Kolmannelle luokalle ja sitä vanhemmille oppilaat ovat sisäistäneet ajatuksen 10:n ja 100:n ryhmästä. He käyttävät näitä rakentaessaan lukuja ja paikka-arvoja tuhanteen asti. Vielä tärkeämpää on, että he käyttävät niitä yhteen- ja vähennyslaskuihin uudelleenryhmittelyn avulla.

LUE LOPPUUN LOPPUUN KATSOAKSESI, KUINKA VOIT VASTAANOTTAA

MAKSUTON PAIKKA-ARVOPELI!

Kolmannella luokalla K – 3 olevilla oppilailla on oltava monia kokemuksia lukujen ilmaisemiseen monin eri tavoin. Oppilaiden tulisi harjoitella saman luvun esittämistä eri kokoonpanoissa. Katso alla oleva esimerkki.

Neljännellä ja viidennellä luokalla perusluvut 10 muuttuvat desimaaliluvuiksi. Tuhatkuutiosta tulee kymppejä ja litteästä ykkösiä, sauvasta kymmenyksiä ja yksikkökuutiosta sadasosia. Se voi olla hämmentävää! Tässä on video, joka selittää sen.

Miten paikka-arvojen opettaminen alkaa?

Se alkaa laskemisesta. Esi- ja päiväkodissa oppilaita opetetaan laskemaan. Laskemiseen liittyy paljon alataitoja ja ymmärrystä: alitusta, merkitsemistä, yksi yhteen – vastaavuutta, hierarkkista sisällyttämistä, sanallista laskemista, ohituslaskentaa, lukumäärien vertailua ja määrien sovittamista lukumäärän vakiomuotoon.

Siitä lähtien paikka-arvon opettaminen (vaikka se ei ehkä näytä sellaiselta) on sitä, että opetetaan lasten- ja ekaluokkalaisille ajatus lukujen koostamisesta ja hajottamisesta sekä kymppien muodostamisesta. Kymmenen tekeminen on ensimmäinen kosketus paikka-arvon opettamiseen muodollisesti.

Niputtaminen ja purkaminen on osa paikka-arvon opettamista

Kun oppilaat osaavat muodostaa kympin, seuraava askel on opettaa oppilaita laskemaan tuo kymppi yhdeksi yksiköksi – yhdeksi kympiksi! Kun teemme näin, se on yksiköintiä. Olen aiemminkin kirjoittanut siitä, että yksikkölaskenta on suuri matematiikan idea. Ajatus siitä, että 10 yksittäistä yksikköä voidaan niputtaa yhdeksi kokonaisuudeksi, on iso matemaattinen ajatus, jonka pienimpien lasten on vaikea käsittää, varsinkin sen jälkeen, kun olemme korostaneet yksi-yhteen vastaavuuden merkitystä. Nyt 10:stä tulee 1!

Yksi erittäin tehokas tapa opettaa yksiköintiä on laskea kokoelmia. Anna heidän vain laskea! He voivat laskea mitä tahansa. Tarkoituksena on, että oppilaat kehittävät tehokkaita laskentajärjestelmiä. He huomaavat, että ryhmittely kymppien ja lopulta satojen mukaan auttaa pitämään kirjaa laskemisesta. He huomaavat, että yhden esineen laskeminen satoihin tai kymmeniin on erittäin tehokas tapa laskea suuria määriä.

Laskukokoelmat paikka-arvojen harjoitteluun

Pitkän aikavälin hyötyjä varten oppilaat pitää saada laskemaan! Jos laskentakokoelmat eivät ole sinulle tuttuja, tutustu tähän verkkosivustoon. Laskukokoelmat ovat loistava tapa saada oppilaat laskemaan mielekkäällä ja hauskalla tavalla. Oppilaat voivat laskea mitä tahansa! Laskukokoelmat sopivat erinomaisesti matematiikkakeskuksiin tai pienryhmätyöskentelyyn. Oppilaat voivat kirjata kokoelmansa kymppikehyksiin, piirtämällä tai kirjoittamalla numeron.

Mitä esineitä voit laskea?

• napit
• paperiliittimet
• lyijykynät
• papupavut
• siemenet
• laskurit
• kuutiot
• laatat

Minun ehdotan, että lähetät vanhemmille kotiin kirjeen, jossa pyydät lahjoituksia napeista, pussi papuja, pähkinöitä ja aluslevyjä, pussi makaronia jne. Oppilaat voivat laskea mitä tahansa. Laita nämä materiaalit pusseihin, joissa on erilaisia määriä oppilaiden tarpeiden mukaan. Anna heidän kirjata tuloksensa tyhjälle kymppiruutu-, satakehys- tai muulle tyhjälle kirjauslomakkeelle.

Sivumennen sanottuna, myös yläkouluikäiset hyötyisivät laskemisesta. Tutustu tähän NCTM:n (National Council of Teachers of Mathematics) artikkeliin ylemmille luokka-asteille tarkoitetuista laskukokoelmista, mukaan lukien kuorolaskenta.

Joitakin tapoja paikka-arvojen opettamiseen

Kun opetat paikka-arvoja oppilaille, ota huomioon seuraavat asiat:

• oppilaan luokka-aste ja standardin erityispiirteet
• sopivien manipulatiivisten välineiden käyttö visuaalisen ja konkreettisen kokemuksen aikaansaamiseksi
• annat oppilaille aikaa!

Kakkos- ja kolmosluokkien oppilailta kestää aikaa sisäistää lukuarvot, koska numerot ovat luonteeltaan vain suureen symbolisia esityksiä. Mutta kun aloitamme konkreettisesta, jotta oppilaat voivat nähdä ja koskettaa matematiikkaa, voimme lujittaa heidän ymmärrystään.

Ei pidä myöskään unohtaa, että kun oppilaat harjoittelevat matematiikan välineillä, kuten 10:n peruslohkoilla tai muilla laskentamateriaaleilla, he käyttävät matemaattisia välineitä (matematiikan harjoittelun standardi 5) etsiäkseen ja hyödyntääkseen paikka-arvojen rakennetta (matematiikan harjoittelun standardi 7). Kun oppilaat ottavat yhdessä muodossa, kuten sanamuodossa, esitetyn luvun ja yrittävät järkeillä abstraktisti ja kvantitatiivisesti (matematiikan harjoittelun standardi 2) esittääkseen kyseisen luvun muissa muodoissa, he mallintavat matematiikkaa (matematiikan harjoittelun standardi 4), koska he käyttävät matemaattisia symboleja (numeroita, laajennettua muotoa, 10:n emäksen yksikköjä) esittäessään määrän. Kuten näet, paikka-arvot ovat loistava tapa saada oppilaat ajattelemaan matemaattisesti.

LUE LOPPUUN LOPPUUN KATSOAKSESI, KUINKA VOIT VASTAANOTTAA

MAKSUTON PAIKKA-ARVOPELI!

Katso tämä video paikka-arvoja koskevista Common Core State Standards for Place Value -standardeista (yhden Common Core -standardien laatijan kanssa!)

Seuraavana on päiväkoti-, ensimmäisen ja toisen luokan tehtäväkohtainen aktiviteetti, jota voit käyttää paikka-arvojen kehittämiseen.

Paikka-arvo lastentarhassa

Lastentarhassa paikka-arvoon liittyvä matematiikan Common Core State Standard for Mathematics -standardi sanoo: Kokoa ja hajota luvut 11-19 kymmeniksi ja ykkösiksi käyttämällä esineitä tai piirroksia ja kirjaa ne piirrokseksi tai yhtälöksi.

Unifix- tai linkkikuutioilla oppilaat voivat rakentaa torneja päästäkseen 10:een. Tässä on hauska aktiviteetti, joka auttaa teinilukujen oppimisessa. Tämä aktiviteetti on tarkoitettu kolmelle oppilaalle, jotka leikkivät yhdessä. Tätä aktiviteettia varten tarvitset vähintään 20-30 Unifix-kuutiota kutakin kolmen hengen ryhmää varten.

Unifix- tai linkkikuutioaktiviteetti

1. Opiskelijat istuvat piirissä Unifix-kuutioiden kasan ympärillä.
2. Vuorotellen kukin nappaa kourallisen YHDELLÄ kädellä.
3. Sitten kukin oppilas laskee, kuinka monta kuutiota kullakin on.
4. Yhteistyössä oppilaat päättävät, kuka kolmesta oppilaasta voi muodostaa kympin yhdistämällä kaksi kourallista. Jos esimerkiksi yhdellä oppilaista olisi 6 kuutiota ja toisella 4 kuutiota, se tekisi kympin. Jos yhdistelmää ei saada aikaan, jokainen laittaa kuutiot takaisin ja yrittää uudestaan toisella kourallisella.
5. Yhdistetään kouralliset, joista saadaan kymppi, junaksi tai torniksi ja lasketaan sitten jäljelle jäävä kämmenmäärä.
6. Yhteistyössä oppilaat laskevat summan sanomalla: ”10 ja ___ muodostavat ____”. Jos esimerkiksi kympin tekemisen jälkeen jäljelle jäi 6 Unifix-kuutiota, he sanovat: ”10 ja 6 tekee 16.”
7. Sitten oppilaat palauttavat kaikki kuutiot kasaan linkittämättöminä ja leikkivät uudestaan.
8. Leikki toistuu.

Variaationa tästä oppilaat työskentelevät itsenäisesti tarttumalla kouralliseen molemmilla käsillä. Sitten oppilas tekee kymppijunan kuutioilla. Yhdessä jäljelle jääneiden kuutioiden kanssa oppilas sanoo, että 10 ja ___ muodostavat ____.” Voit myös pyytää oppilaita kirjaamaan lukumääränsä muistiinpanolomakkeelle.

LUE LOPUKSI, ETTÄ LOPPUUN LÖYDÄT, KUINKA VOIT VASTAANOTTAA

MAKSUTON PAIKKA-ARVO-PELIN!

Paikka-arvot ekaluokalla

Ensimmäisellä luokalla paikka-arvoihin liittyvässä matematiikan yhteisessä perusopetuksen laatimisessa (Common Core State Standard for Mathematics for Place Value) sanotaan: Ymmärtää, että kaksinumeroisen luvun kaksi numeroa edustavat kymmenien ja ykkösten määriä.

Kymmenen yksikön niputtaminen yhdeksi kympiksi on osa tätä standardia. Niputtaminen on yksiköintiä. Tässä on aktiviteetti, jolla kehitetään niputtamista ja kymppien ja ykkösten ymmärtämistä. Tätä aktiviteettia varten tarvitset yhden korttisarjan, jossa on numerot 11 – 99, niputettuja kymppejä ja kuutioita tai laskureita tai mitä tahansa, mitä voidaan laskea yksiköiksi. Tarvitset myös kaksoissarjan numerokortteja.

Niputusaktiviteetti

1. Jaa luokka kahtia. Toinen puolikas tulee eteen, toinen puolikas pysyy paikoillaan.
2. Jaa yksi numerokortti jokaiselle istuvalle lapselle. Jokaisesta jakamastasi kortista pidä kaksoiskappale sivussa seisoville oppilaille.
3. Istuvat lapset muodostavat kortissa olevan luvun kymppinippujen ja yksiköiden avulla. Käännä sitten heidän korttinsa kuvapuoli alaspäin.
4. Kun kaikki istuvat oppilaat ovat rakentaneet numeronsa, anna seisoville oppilaille yksi kaksoiskortti.
5. Sisällä seisovat oppilaat löytävät nyt numeron, jonka yksi oppilaista on rakentanut. Kun he ovat löytäneet numeronsa, he asettuvat toisen oppilaan taakse.
6. Kun kaikki oppilaat ovat löytäneet numeronsa, istuvat oppilaat kääntävät korttinsa ja katsovat, vastaavatko ne seisovan oppilaan korttia.
7. Kysy istuvilta oppilailta, mistä he tiesivät, kuinka monta kymppiä ja ykköstä on käytettävä luvun muodostamiseen, ennen kuin toistat toisen vuoron. Kysy seisovilta oppilailta, mistä he tiesivät löytäneensä sopivan luvun.
8. Sisallaan seisovat oppilaat vaihtavat nyt istuvien oppilaiden kanssa ja toistavat prosessin.

Käyttäkää laskentakokoelmia harjoitellaksenne yksiköintiä ja rakentaaksenne paikka-arvotietoa. Katso edellä kohdassa Paikka-arvot päiväkodissa, miten laskentakokoelmia voi käyttää.

Toinen huomioon otettava tekijä paikka-arvojen opettamisessa on opettaa oppilaita piirtämään niput tai perus 10:n palikat. Esimerkiksi kymppiä edustava sauva on vain viiva, kun taas yksiköitä tai ykkösiä edustavat kuutiot ovat vain neliöitä. Perus 10:n palikoiden piirtäminen noudattaa CRA:n mallia konkreettinen-edustava-abstrakti.

Paikka-arvo toisella luokalla

Kakkosluokalla paikka-arvoon liittyvässä matematiikan Common Core State Standard for Mathematics -standardissa sanotaan: Ymmärtää, että kolminumeroisen luvun kolme numeroa edustavat satojen, kymmenien ja ykkösten määriä.

Kakkosluokan standardia on laajennettu siten, että se kattaa nyt myös sadat. Mutta jotta oppilaat pääsevät satoihin, heillä on oltava vankka perusta kymppien ja ykkösten kanssa. Tämän perustan tulisi koostua kymppiryhmän niputtamisen ja purkamisen käsitteestä sekä minkä tahansa luvun esittämisestä monissa yhdistelmissä: 43 voi olla 4 kymppiä ja 3 ykköstä, mutta myös 3 kymppiä ja 13 ykköstä tai 2 kymppiä ja 23 ykköstä tai 1 kymppi ja 33 ykköstä tai jopa 43 ykköstä.

Kakkosluokkalaisten osalta haluamme, että he niputtavat 10 kymppiryhmää sadaksi. Tässä on tehtävä, jolla harjoitellaan kymppien niputtamista satasiksi. Tätä aktiviteettia varten tarvitset korttisarjan 0-9 (2 kappaletta kutakin, yhteensä 20 korttia), perusta 10:n palikoita (yksiköitä, sauvoja ja litteitä) ja paikka-arvomaton. Oppilaat voivat pelata yksin, pareittain tai ryhmässä. Tavoitteena on päästä tiettyyn lukumäärään. Voit päättää lukumäärän peliin varatun ajan perusteella(pelaa 300:aan, 400:aan, 500:aan tai useampaan).

Kymppiryhmien niputtaminen Activity

1. Opiskelija valitsee kaksi numerokorttia. Oppilas päättää, mikä numero soitetaan. Jos esimerkiksi valitsen 5 ja 2, se voi olla 52 tai 25. Jos tavoitteeni on päästä tiettyyn, valitsen suuremman luvun.
2. Opiskelija rakentaa sitten luvun käyttäen 10-kantaisia palikoita paikka-arvomattoon.
3. Jos leikkii muiden oppilaiden kanssa, muut tekevät vuorollaan saman.
4. Kun oppilaalla on 10 palikkaa, hänen on niputettava kymppitanko. Kun oppilaalla on 10 sauvaa, oppilaan on niputettava ne tasaiseksi tai 100:ksi.
5. Ensimmäinen oppilas, joka saavuttaa määrätyn määrän, voittaa. Sitten muut asetetaan paremmuusjärjestykseen sen perusteella, kenellä on seuraavaksi korkein yhteissumma jne.

LUE LOPUKSI LOPUKSI, niin saat

VAPAA PAIKKA-ARVO-PELI!

Paikka-arvo saa nyt uusia muotoja

Kakkosluokkalaiset esittävät lukuja myös muilla tavoilla kuin vain 10:n perustan palikoilla. He oppivat ilmaisemaan kolminumeroisia lukuja vakiomuodossa, laajennetussa muodossa, sanamuodossa ja perus 10 -yksiköissä (esim. 236:ssa on 2 sataa, 3 kymmentä ja 6 ykköstä). Luku voi siirtyä konkreettisesta abstraktiin riippuen siitä, miten se esitetään, kuten alla olevasta taulukosta käy ilmi.

Kun oppilaat oppivat lukuarvoja, haluamme heidän siirtyvän konkreettisesta abstraktiin hitaasti. Emme halua liittää numeroita paikka-arvotaulukkoon ja kysyä, kuinka monta sataa, kymppiä ja ykköstä. Sen sijaan haluamme edetä kohti abstraktia. Kun oppilaat esittävät lukuja laajennetussa muodossa, he näkevät numeroiden arvot. Esimerkiksi 394 on sama kuin 300 + 90 + 4. Jokainen numero tuossa luvussa kirjoitetaan arvona, joten on selvää, että 3 ei ole vain 3 vaan 300 ja niin edelleen.

Pohjata paikka-arvot konkreettisesti

Työskennellessään 10:n perusyksiköissä oppilaat voivat ottaa saman luvun ja sanoa, että 3 on sadasosassa, joten se on 3 sataa, 9 kymppiä ja 4 ykköstä. Tämä on abstraktimpi tapa esittää luku, koska oppilaiden on mielessään visualisoitava sadat kahdella nollalla, kympit yhdellä nollalla ja ykköset yksinumeroina. Yksi tapa vahvistaa tätä visualisointia on yhdistää laajennettu ja vakiomuoto 10:n perusyksiköihin.

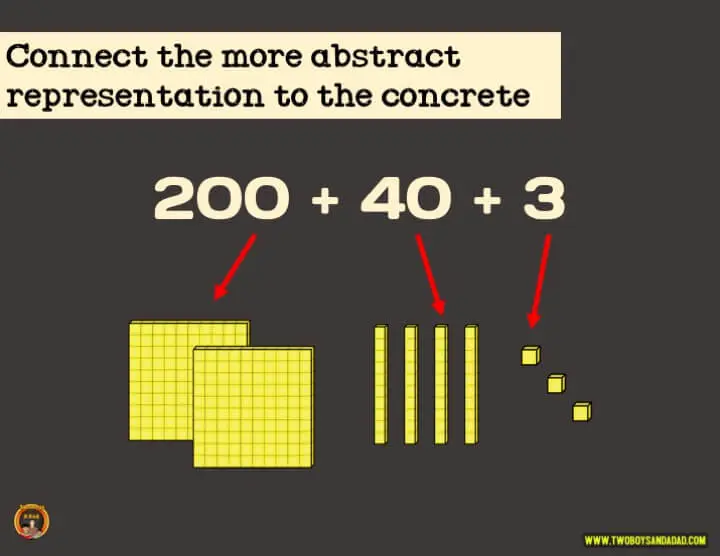
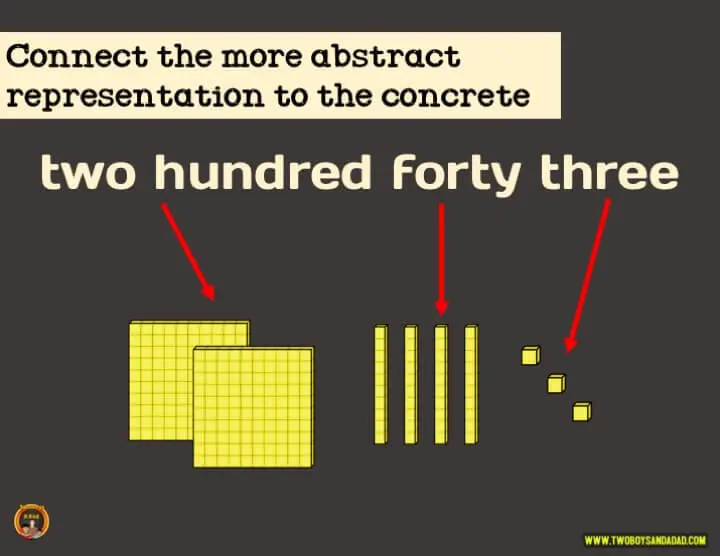
Mennään vielä abstraktimpaan esitystapaan sanamuodossa. Sanamuoto voi olla sikäli ongelmallinen, että jos lapsi ei osaa lukea sanoja, asia muuttuu epäselväksi. Mutta jos lapsi pystyy lukemaan sanoja, 394:n kirjoittaminen sanamuodossa (kolmesataa yhdeksänkymmentäneljä) voi olla haastavaa, jos se tulkitaan väärin. Esimerkiksi 394:n sanamuodon sanominen saatetaan tulkita 30094:ksi (kolmesataa ja sitten 94).

Jotta oppilaat oppisivat tunnistamaan lukuja ja niiden arvoja sanamuodossa, yhdistä se johonkin vähemmän abstraktiin, kuten 10:n peruslohkoihin tai laajennettuun muotoon.

Viimeiseksi, kun oppilaat ymmärtävät numeroiden arvot kunnolla, voit siirtyä paikka-arvotietotauluun. Siihen mennessä heidän pitäisi olla sisäistäneet tai pystyä visualisoimaan numeroiden arvo pelkästään katsomalla niiden paikkaa luvussa. Jos siis aloitat paikka-arvojen opettamisen paikka-arvotaulukolla, olet aloittanut paikka-arvojen abstraktimmasta esitystavasta. Siksi pitäisin sitä vääränä tapana aloittaa.

Lähteitä paikka-arvojen opettamiseen

Opetettuani äskettäin toista luokkaa ja seitsemän vuotta ensimmäistä luokkaa tiedän, miten tärkeää on tehdä käsitteistä konkreettisia ja visuaalisia, jotta oppilaat voivat ymmärtää ne. Siksi kehitin nämä paikkatietoaineistot toiselle luokalle. Ne koostuvat

• 4-osaisesta PowerPoint-esityksestä, jolla opetetaan paikka-arvoa 2- ja 3-numeroisilla luvuilla
• palapelikeskuksesta paikka-arvon harjoitteluun
• 4 pelistä paikka-arvon hallitsemiseksi

Paikka-arvon PowerPoint-oppitunnit

PowerPoint-opetus koostuu kahdesta oppitunnista, joista toinen käsittelee kaksinumeroisia lukuja ja toinen kolminumeroisia lukuja. PowerPoint on suunniteltu kehittämään lukuarvoja konkreettisista malleista abstraktimpiin malleihin. Animaation, ohjatun harjoittelun ja itsenäisen harjoittelun avulla oppilaille näytetään, miten lukua voidaan esittää laajennetussa muodossa, perus 10 -yksiköissä, sanamuodossa ja perus 10 -lohkoissa. Yksityiskohtaiset puhujamerkinnät opettajalle sisältävät opetuskohtia ja kysymyksiä matemaattisen ajattelun stimuloimiseksi. Mukana tulostettavia harjoitusdioja, jotka vaihtelevat syvyysluokkien 1 – 3 välillä.

Place Value Puzzle Center

Palapelikeskuksessa harjoitellaan kaksi- ja kolminumeroisten lukujen esittämistä eri muodoissa. Oppilaat eivät ainoastaan laita palapelejä yhteen, vaan heidän on myös selitettävä, mistä he tietävät, että kaikki palapelin palat edustavat samaa lukua. Käytä palapelejä koko luokan tehtävänä, pareittain tai itsenäisenä matematiikkakeskuksena. Mukana on kirjauslomakkeet, vastausavaimet, ohjeet ja tukimateriaalit.

Place Value Games

Peliresurssi sisältää neljä peliä, joiden avulla voidaan harjoitella paikka-arvojen hallintaa (jokaisesta pelistä on kaksi- ja kolminumeroinen versio). Joissakin peleissä oppilaan on ilmoitettava numeron arvo tai ratkaistava arvoitus, joka perustuu paikka-arvoon. Yhdessä pelissä on osoitettava paikka-arvon ymmärtämistä vertailemalla lukuja, jotka on esitetty eri esitystavoissa, kuten sanamuodossa, laajennetussa muodossa, perus 10:n lohkoissa ja perus 10:n yksiköissä.

Paikka-arvopalapeli Google Slides®

Jos oppilaillasi on käytössään Chromebookit, kannettavat tietokoneet, pöytätietokoneet tai tablettitietokoneet, voit laittaa heidät harjoittelemaan paikka-arvoja Google Slidesissa. Mukana on yli 60 diaa, jotka on jaettu kahteen osaan: 2-numeroisten lukujen ja 3-numeroisten lukujen harjoittelu. Oppilaat harjoittelevat numeroiden esittämistä vakiomuodossa, laajennetussa muodossa, sanamuodossa ja 10:n perusyksikössä.

Useimmissa resursseissa on ehdotettu tai niihin on sisällytetty tukea englannin kielen oppijoille ja vammaisille oppilaille.

Liity ja saat ILMAISEN bonuspelin

Saa ILMAISEN bonuspelin paikka-arvon opettamiseen! Tein tämän eksklusiivisen FREEBIE-pelin, jota voi käyttää paikka-arvojen harjoitteluun päiväkodissa, ensimmäisellä luokalla ja toisella luokalla! Käytä samaa peliä kaikilla luokka-asteilla. Käytä vain ilmaispeliin sisältyviä luokka-astekortteja pelaamiseen.

Tilaa alla oleva uutiskirjeeni ja saat tämän Paikka-arvojen bonuspelin!

Älkää vielä lähtekö!

Oletko aloittanut 1:1-luokkahuoneessa? Sitten sinun kannattaa lukea arvokkaat vinkkini 1:1-luokkahuoneeseen.

Katso, miten käytän Google Classroomia esitelläkseni vanhempainillassa Back to School Night for Parents.

Tilaa uutiskirjeeni ja saat tämän CONTROL KEYS Shortcut -julisteen ILMAISEKSI. Tilaa vain uutiskirjeeni alla, ja saat myös bonuksena oppilaan työpöytäversion! Rekisteröidy nyt!

Vai rekisteröidy uutiskirjeeseen saadaksesi tämän ILMAISEN oppaan kertolaskun sujuvuuden saavuttamiseen. Hanki se nyt kirjautumalla alla olevaan uutiskirjeeseeni!