Yksinkertainen kuvaus
Käsitellään ensin eteenin pi-sidosta yksinkertaistetun MO-teorian näkökulmasta (tässä esimerkissä jätämme huomiotta molekyylin sigma-sidokset ja ajattelemme vain π-sidosta). Aloitamme kahdesta atomiorbitaalista: yksi hybridiytymätön 2p-orbitaali kummastakin hiilestä. Kumpikin sisältää yhden elektronin. MO-teoriassa nämä kaksi atomia yhdistyvät matemaattisesti muodostaen kaksi pi-molekyyliorbitaalia, joista toinen on matalaenerginen pi-sidosorbitaali ja toinen korkeaenerginen pi*-antibondiorbitaali.

Eteenin (etyleenin)
Molekyyliorbitaalit
Sidoksellisessa pi-orbitaalissa p-orbitaalien kaksi tummennettua lohkoa vuorovaikuttavat konstruktiivisesti toistensa kanssa, samoin kuin kaksi tummennettua lohkoa (muistakaa, että mielivaltainen tummennusvalinta edustaa matemaattisia (+)- ja (-) -merkkejä matemaattisessa aaltofunktiossa, joka kuvaa orbitaalia). Molempien hiiliytimien välillä on lisääntynyt elektronitiheys molekyyliorbitaalissa – kyseessä on sidosvuorovaikutus.
Korkeamman energian antisidoksisessa pi*-orbitaalissa toisen p-orbitaalin tummennettu lohko vuorovaikuttaa destruktiivisesti toisen p-orbitaalin tummennetun lohkon kanssa, mikä johtaa solmuun molempien ytimien välille ja yleiseen hylkimiseen hiiliytimien välillä.
Käyttämällä taas ”rakentamisperiaatetta” sijoitamme kaksi elektronia matalamman energian omaavaan, sitovaan pi-molekyyliorbitaaliin. Antibonding pi*-orbitaali jää tyhjäksi.
Eteenin yksityiskohtaisempi MO-kuvaus
Molekyyliorbitaaliteoriaa on sovellettu hyvin menestyksekkäästi suuriin konjugoituneisiin systeemeihin, erityisesti niihin, jotka sisältävät hiiliatomien ketjuja, joissa on vuorottelevia yksinkertaisia ja kaksinkertaisia sidoksia. Hückelin vuonna 1931 esittämässä approksimaatiossa otetaan huomioon vain delokalisoituneet p-elektronit, jotka liikkuvat \pi -sidosten kehyksessä. Tämä on itse asiassa kehittyneempi versio vapaiden elektronien mallista. Orgaanisen kemian johdantokurssilla ei tarvitse käyttää kaikkea Hückelin matematiikkaa, mutta niille, jotka haluavat päästä syvemmälle, annetaan tässä yksityiskohtaisempi analyysi.
Yksinkertaisin tarkasteltava hiilivety, jolla on \pi-sidoksia, on eteni (etyleeni), joka koostuu neljästä vetyatomista ja kahdesta hiiliatomista. Kokeellisesti tiedämme, että eteenin H-C-H- ja H-C-C-kulmat ovat noin 120°. Tämä kulma viittaa siihen, että hiiliatomit ovat sp2-hybridisoituneita, mikä tarkoittaa, että yhden hiilen yksittäin varattu sp2-orbitaali on päällekkäin kunkin H:n yksittäin varattujen s-orbitaalien ja toisen C:n yksittäin varattujen sp2-orbitaalien kanssa. Näin ollen kukin hiili muodostaa joukon kolmea \sigma-sidosta: kaksi C-H:ta (sp2 + s) ja yhden C-C:n (sp2 + sp2) (alla olevan kuvion 13.1. osa (a).).
 >
>
Kuva 13.1. (a) σ-sidoksinen kehys muodostuu kahden yksittäin miehitetyn hiilen sp2-hybridiorbitaalien sarjan ja neljän yksittäin miehitetyn vedyn 1s-orbitaalin päällekkäisyydestä elektroniparisidosten muodostamiseksi. Tämä käyttää 10 valenssielektronia 12:sta muodostaakseen yhteensä viisi σ-sidosta (neljä C-H-sidosta ja yksi C-C-sidos). (b) Kumpaankin hiiliatomiin jää yksi yksittäin miehitetty hybridiytymätön 2pz-orbitaali muodostamaan hiili-hiili π-sidoksen. (Huomautus: Konvention mukaan tasomaisissa molekyyleissä molekyylitasoon nähden kohtisuorassa oleva akseli on z-akseli.)
Hückelin approksimaatiota käytetään konjugoitujen systeemien \pi-molekyyliorbitaalien energioiden ja muotojen määrittämiseen. Hückelin approksimaatiossa näiden hiilivetyjen kovalenttiset sidokset voidaan erottaa kahteen itsenäiseen ”kehykseen”: \sigma -sidoskehykseen ja \sigma -sidoskehykseen. Kummassakin kehyksessä sidosorbitaalien kuvaamiseen käytetyt aaltofunktiot johtuvat atomiorbitaalien erilaisista yhdistelmistä. Menetelmä rajoittuu käsittelemään konjugoituja hiilivetyjä, ja siinä otetaan erityisesti huomioon vain \pi-elektronien molekyyliorbitaalit, koska ne määräävät näiden molekyylien yleiset ominaisuudet; sigmaelektronit jätetään huomiotta. Tätä kutsutaan sigma-pi-erotettavuudeksi, ja se on perusteltua, koska \sigma- ja \pi-orbitaalit ovat ortogonaalisia tasomolekyyleissä. Tästä syystä Hückel-menetelmä rajoittuu planaarisiin systeemeihin. Hückelin approksimaatiossa oletetaan, että \pi-sidosten elektronit ”tuntevat” sähköstaattisen potentiaalin, joka johtuu molekyylin koko \sigma-sidoskehyksestä (eli siinä keskitytään vain \pi-sidosten muodostumiseen, koska \sigma-sidoskehys on jo muodostunut).
Konjugoituneet systeemit
Konjugoituneessa systeemissä on alue, jossa on päällekkäisiä p-orbitaaleja, jotka silloittavat vierekkäisiä yksittäisiä sidoksia ja jotka mahdollistavat \pi-elektronien delokalisaation kaikkien vierekkäisten linjassa olevien p-orbitaalien yli. Nämä \pi-elektronit eivät kuulu yksittäiseen sidokseen tai atomiin, vaan pikemminkin atomiryhmään.
Eteeni
Ennen kuin tarkastelemme eteenin Hückel-käsittelyä, on hyödyllistä käydä läpi molekyylin yleinen sidoskuva. Eteenissä tapahtuvaan sitoutumiseen liittyy jokaisen hiiliatomin 2s , 2p_x ja 2p_y atomiorbitaalien sp^2-hybridisaatio; 2p_z-orbitaalit jäävät koskemattomiksi (kuva 13.2).
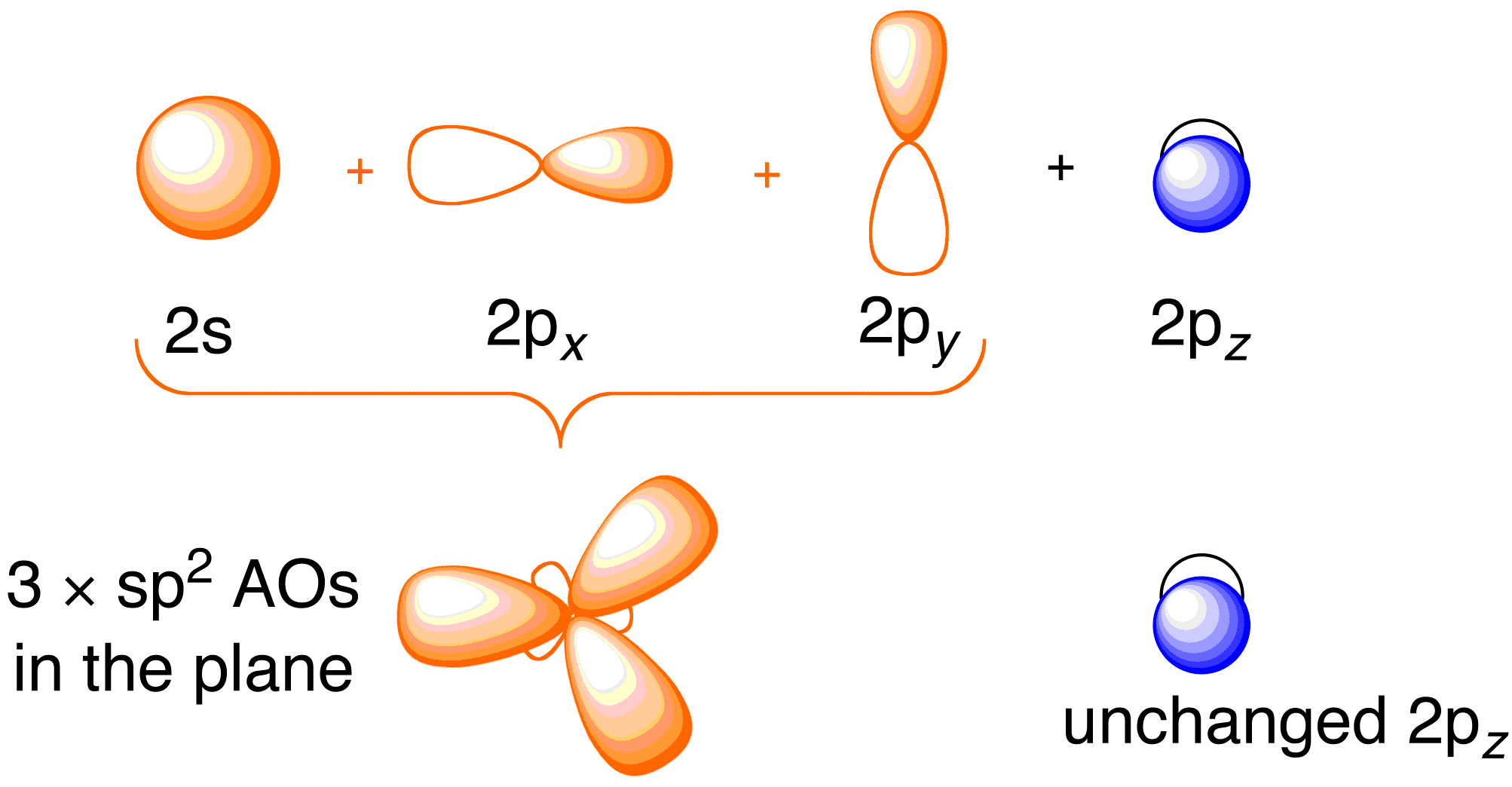
Kuva 13.2. Hiilen atomiorbitaalien hybridisointi sp^2-hybridiorbitaalien aikaansaamiseksi vetyatomeihin sitoutumista varten eteenissä. Kuvaa on käytetty luvalla ChemTubesta (CC-SA-BY-NC; Nick Greeves).
Hybridiorbitaalien käyttö tässä kuvatussa molekyyliorbitaalilähestymistavassa on vain tarkoituksenmukaista eikä siinä vedota valenssisidosteoriaan (suoraan). Identtinen kuvaus voidaan saada käyttämällä yksinomaan hiilen atomiorbitaaleja, mutta tuloksena saatavien aaltofunktioiden tulkinta on vähemmän intuitiivinen. Esimerkiksi iides molekyyliorbitaali voidaan kuvata hybridiorbitaalien
\
tai atomiorbitaalien avulla.
\
missä \{a_i\} ja \{c_i\} ovat laajenemiskertoimia. Kumpikin kuvaus toimii ja molemmat ovat identtisiä lähestymistapoja, koska
\
jossa \{c_i\} ovat hybridisoitua orbitaalia kuvaavia kertoimia.
Sitoutuminen tapahtuu hiilen sp^2 -hybridiorbitaalien elektronien ja neljän vetyatomin 1s -atomiorbitaalien elektronien sekoittumisen kautta (kuva 13.2. ylhäällä vasemmalla), jolloin syntyy \sigma -sitoutumiskehys. \pi -sidosrakenne syntyy hybridiytymättömistä 2p_z-orbitaaleista (kuva 13.2. yllä oikealla). Näiden kahden kehyksen riippumattomuus näkyy tuloksena olevasta molekyyliorbitaalidiagrammista alla olevassa kuvassa; Hückelin teoria käsittelee vain \pi-sidoksen molekyyliorbitaalien ja energioiden kuvaamista.

Kuva 13.3. \pi-sidoksen molekyyliorbitaalit ja energiat: Molekyyliorbitaalit, jotka osoittavat etyleenin \pi -sidospuitteiden (sininen) ja \sigma -sidospuitteiden (punainen) sigma-pi-erotettavuuden.
Hückelin käsittelyssä on kyse vain \pi-sidoskehikon molekyyliorbitaalien ja energioiden kuvaamisesta.
Koska Hückelin teoria on molekyyliorbitaaliteorian erityiskäsittely, molekyyliorbitaalit | \psi_i \rangle voidaan kuvata hiilen 2p_z-atomiorbitaalien \phi lineaarisena kombinaationa vastaavien \{c_i\}-kertoimien kanssa:
\
Täydellinen kvanttikemian analyysi Schrödingerin yhtälön avulla (ei vaadita orgaanisen kemian kurssilla), katso tämä Libretexts-sivu.
Nämä molekyyliorbitaalit muodostavat π-sidoksen kehikon, ja koska jokainen hiili tuottaa yhden elektronin tähän kehikkoon, vain alin molekyyliorbitaali ( | \psi_1 \rangle ) on varattu (kuva ) perustilassa. Vastaava elektronikonfiguraatio on tällöin \pi_1^2 .

Kuva 13.4: Etyleenin \pi-molekyyliorbitaalien kehyksen kaavamainen esitys . Huomaa, että antisitovalla molekyyliorbitaalilla on odotetusti yksi solmu enemmän kuin sitovalla molekyyliorbitaalilla, koska sen energia on korkeampi.
HOMO ja LUMO ovat lyhenteitä korkeimmin miehitetylle molekyyliorbitaalille (highest occupied molecular orbital) ja alimmalle miehittämättömälle molekyyliorbitaalille (lowest unoccupied molecular orbital), ja niihin viitataan usein nimellä rajapintaorbitaalit. HOMO:n ja LUMO:n välistä energiaeroa kutsutaan HOMO-LUMO-aukoksi.
Kolmiulotteisesti lasketut \pi-molekyyliorbitaalit on esitetty kuvassa 13.5.

Kuva 13.5: Eteenin lasketut \pi-molekyyliorbitaalit . (Vasemmalla) sidosorbitaali (ψ1) ja (oikealla) antisidonnainen (ψ2) orbitaali.
Tekijät
- Seymour Blinder (kemian ja fysiikan emeritusprofessori Michiganin yliopistosta, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
