Analyse de régression logistique

Le résultat dans l’analyse de régression logistique est souvent codé comme 0 ou 1, où 1 indique que le résultat d’intérêt est présent, et 0 indique que le résultat d’intérêt est absent. Si nous définissons p comme la probabilité que le résultat soit 1, le modèle de régression logistique multiple peut être écrit comme suit :

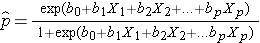
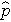est la probabilité attendue que le résultat soit présent ; X1 à Xp sont des variables indépendantes distinctes ; et b0 à bp sont les coefficients de régression. Le modèle de régression logistique multiple est parfois écrit différemment. Sous la forme suivante, le résultat est le logarithme attendu de la probabilité que le résultat soit présent,

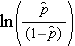
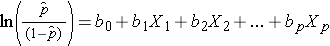
Notez que le côté droit de l’équation ci-dessus ressemble à l’équation de régression linéaire multiple. Cependant, la technique d’estimation des coefficients de régression dans un modèle de régression logistique est différente de celle utilisée pour estimer les coefficients de régression dans un modèle de régression linéaire multiple. Dans la régression logistique, les coefficients dérivés du modèle (par exemple, b1) indiquent la variation de la probabilité logarithmique attendue par rapport à une variation d’une unité de X1, tous les autres prédicteurs restant constants. Par conséquent, l’antilogue d’un coefficient de régression estimé, exp(bi), produit un rapport de cotes, comme illustré dans l’exemple ci-dessous.

Exemple de régression logistique – Association entre l’obésité et les MCV

Nous avons précédemment analysé les données d’une étude conçue pour évaluer l’association entre l’obésité (définie comme IMC > 30) et les maladies cardiovasculaires incidentes. Les données ont été recueillies auprès de participants âgés de 35 à 65 ans et exempts de maladie cardiovasculaire (MCV) au départ. Chaque participant a été suivi pendant 10 ans pour le développement de la maladie cardiovasculaire. Un résumé des données se trouve à la page 2 de ce module. Le risque relatif non ajusté ou brut était RR = 1,78, et le rapport de cotes non ajusté ou brut était OR = 1,93. Nous avons également déterminé que l’âge était un facteur de confusion, et en utilisant la méthode de Cochran-Mantel-Haenszel, nous avons estimé un risque relatif ajusté de RRCMH =1,44 et un odds ratio ajusté de ORCMH =1,52. Nous allons maintenant utiliser l’analyse de régression logistique pour évaluer l’association entre l’obésité et les maladies cardiovasculaires incidentes en ajustant pour l’âge.

L’analyse de régression logistique révèle les éléments suivants :

Variable indépendante	Coefficient de régression	Chi-carré	P-valeur
Intercept	-2.367	307.38	0.0001
Obesité	0,658	9,87	0.0017

Le modèle de régression logistique simple relie l’obésité aux probabilités logarithmiques de MCV incidentes :

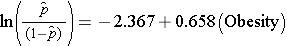
L’obésité est une variable indicatrice dans le modèle, codée comme suit : 1=obèse et 0=non obèse. La probabilité logarithmique de MCV incidente est 0,658 fois plus élevée chez les personnes obèses que chez les personnes non obèses. Si l’on prend l’antilog du coefficient de régression, exp(0,658) = 1,93, on obtient le rapport de cotes brut ou non ajusté. La probabilité de développer une MCV est 1,93 fois plus élevée chez les personnes obèses que chez les personnes non obèses. L’association entre l’obésité et les MCV incidentes est statistiquement significative (p=0,0017). Il convient de noter que les statistiques de test permettant d’évaluer la signification des paramètres de régression dans l’analyse de régression logistique sont basées sur les statistiques du chi carré, et non sur les statistiques t comme c’était le cas avec l’analyse de régression linéaire. Cela s’explique par le fait qu’une technique d’estimation différente, appelée estimation du maximum de vraisemblance, est utilisée pour estimer les paramètres de régression (Voir Hosmer et Lemeshow3 pour des détails techniques).

De nombreux progiciels de calcul statistique génèrent également des rapports de cotes ainsi que des intervalles de confiance à 95 % pour les rapports de cotes dans le cadre de leur procédure d’analyse de régression logistique. Dans cet exemple, l’estimation du rapport de cotes est de 1,93 et l’intervalle de confiance à 95 % est de (1,281, 2,913).

Lorsque nous avons examiné l’association entre l’obésité et les MCV, nous avons précédemment déterminé que l’âge était un facteur de confusion.Le modèle de régression logistique multiple suivant estime l’association entre l’obésité et les MCV incidentes, en ajustant pour l’âge. Le modèle suivant de régression logistique multiple estime l’association entre l’obésité et les MCV incidentes, en tenant compte de l’âge. Dans le modèle, nous considérons à nouveau deux groupes d’âge (moins de 50 ans et 50 ans et plus). Pour l’analyse, le groupe d’âge est codé comme suit : 1=50 ans et plus et 0=moins de 50 ans.

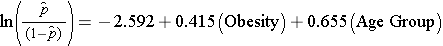
Si nous prenons l’antilog du coefficient de régression associé à l’obésité, exp(0,415) = 1,52 nous obtenons l’odds ratio ajusté pour l’âge. La probabilité de développer une MCV est 1,52 fois plus élevée chez les personnes obèses que chez les personnes non obèses, après ajustement pour l’âge. Dans la section 9.2, nous avons utilisé la méthode de Cochran-Mantel-Haenszel pour générer un odds ratio ajusté pour l’âge et nous avons trouvé ce qui suit :

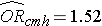
Ceci illustre comment l’analyse de régression logistique multiple peut être utilisée pour tenir compte des facteurs de confusion. Les modèles peuvent être étendus pour tenir compte de plusieurs variables confondantes simultanément. L’analyse de régression logistique multiple peut également être utilisée pour évaluer les facteurs de confusion et la modification de l’effet, et les approches sont identiques à celles utilisées dans l’analyse de régression linéaire multiple. L’analyse de régression logistique multiple peut également être utilisée pour examiner l’impact de plusieurs facteurs de risque (par opposition à la focalisation sur un seul facteur de risque) sur un résultat dichotomique.

Exemple – Facteurs de risque associés à un faible poids de naissance du nourrisson

Supposons que les enquêteurs s’intéressent également aux résultats indésirables de la grossesse, notamment le diabète gestationnel, la pré-éclampsie (c’est-à-dire l’hypertension induite par la grossesse) et le travail prématuré. Rappelons que l’étude porte sur 832 femmes enceintes qui fournissent des données démographiques et cliniques. Dans l’échantillon de l’étude, 22 (2,7 %) femmes développent une pré-éclampsie, 35 (4,2 %) un diabète gestationnel et 40 (4,8 %) un travail prématuré. Supposons que nous souhaitions évaluer s’il existe des différences dans chacune de ces issues défavorables de la grossesse en fonction de la race/ethnie, ajustées pour l’âge maternel. Trois analyses de régression logistique distinctes ont été effectuées, mettant en relation chaque résultat, considéré séparément, avec les trois variables indicatrices ou fictives reflétant la race de la mère et son âge, en années. Les résultats sont présentés ci-dessous.

Suite : Pré-éclampsie	Coefficient de régression	Chi-carré	P-value	Odds Ratio (95% CI)
Intercept	-3.066	4.518	0.0335	–
Race noire	2,191	12,640	0,0004	8.948 (2,673, 29,949)
Race hispanique	-0,1053	0,0325	0,8570	0.900 (0,286, 2,829)
Autre race	0,0586	0,0021	0.9046	1,060 (0,104, 3,698)
Age de la mère (ans)	-0,0252	0.3574	0,5500	0,975 (0,898, 1,059)

La seule différence statistiquement significative en matière de pré-éclampsie se situe entre les mères noires et les mères blanches.

Les mères noires sont près de 9 fois plus susceptibles de développer une pré-éclampsie que les mères blanches, après ajustement pour l’âge maternel. L’intervalle de confiance à 95% pour le rapport de cotes comparant les femmes noires aux femmes blanches qui développent une pré-éclampsie est très large (2,673 à 29,949). Ceci est dû au fait qu’il y a un petit nombre de résultats (seulement 22 femmes développent une pré-éclampsie dans l’échantillon total) et un petit nombre de femmes de race noire dans l’étude. Ainsi, cette association doit être interprétée avec prudence.

Bien que le rapport de cotes soit statistiquement significatif, l’intervalle de confiance suggère que l’ampleur de l’effet pourrait aller d’une augmentation de 2,6 fois à une augmentation de 29,9 fois. Une étude plus importante est nécessaire pour générer une estimation plus précise de l’effet.

Diabète gestationnel	Coefficient de régression	Chi-carré	P-valeur	Odds Ratio (95% CI)
Intercept	-5.823	22,968	0,0001	–
Race noire	1,621	6.660	0,0099	5,056 (1,477, 17,312)
Race hispanique	0,581	1.766	0,1839	1,787 (0,759, 4,207)
Autre race	1,348	5.917	0,0150	3,848 (1,299, 11,3)
Age de la mère (ans)	0,071	4.314	0,0378	1,073 (1,004, 1,147)

En ce qui concerne le diabète gestationnel, il existe des différences statistiquement significatives entre les mères noires et blanches (p=0,0099) et entre les mères qui se déclarent d’une autre race par rapport aux blanches (p=0,0150), ajustées pour l’âge de la mère. L’âge de la mère est également statistiquement significatif (p=0,0378), les femmes plus âgées étant plus susceptibles de développer un diabète gestationnel, après ajustement en fonction de la race/ethnicité.

Résultat : Travail prématuré	Coefficient de régression	Chi-carré	P-valeur	Odds Ratio (IC 95%)
Intercept	-1.443	1.602	0.2056	–
Race noire	-0,082	0,015	0.9039	0,921 (0,244, 3,483)
Race hispanique	-1,564	9.497	0,0021	0,209 (0,077, 0,566)
Autre race	0.548	1,124	0,2890	1,730 (0,628,4,767)
Age de la mère (ans).)	00,037	1,198	0,2737	0,963 (0,901, 1,030)

En ce qui concerne le travail avant terme, la seule différence statistiquement significative est entre les mères hispaniques et blanches (p=0,0021). Les mères hispaniques sont 80 % moins susceptibles de développer un travail avant terme que les mères blanches (odds ratio = 0,209), ajusté pour l’âge de la mère.

Les méthodes multivariables sont complexes sur le plan informatique et nécessitent généralement l’utilisation d’un progiciel de calcul statistique. Les méthodes multivariables peuvent être utilisées pour évaluer et ajuster les facteurs de confusion, pour déterminer s’il y a une modification de l’effet, ou pour évaluer les relations de plusieurs facteurs d’exposition ou de risque sur un résultat simultanément. Les analyses multivariables sont complexes et doivent toujours être planifiées pour refléter les relations biologiquement plausibles. Bien qu’il soit relativement facile de prendre en compte une variable supplémentaire dans un modèle de régression linéaire multiple ou logistique multiple, seules les variables cliniquement significatives devraient être incluses.

Il est important de se rappeler que les modèles multivariables ne peuvent qu’ajuster ou tenir compte des différences dans les variables confondantes qui ont été mesurées dans l’étude. En outre, les modèles multivariables ne doivent être utilisés pour tenir compte des facteurs de confusion que lorsqu’il existe un certain chevauchement dans la distribution du facteur de confusion de chacun des groupes de facteurs de risque.

Les analyses stratifiées sont très informatives, mais si les échantillons de strates spécifiques sont trop petits, les analyses peuvent manquer de précision. Lors de la planification des études, les investigateurs doivent prêter une attention particulière aux modificateurs d’effet potentiels. Si l’on soupçonne qu’une association entre une exposition ou un facteur de risque est différente dans des groupes spécifiques, l’étude doit être conçue pour garantir un nombre suffisant de participants dans chacun de ces groupes. Des formules de taille d’échantillon doivent être utilisées pour déterminer le nombre de sujets requis dans chaque strate pour assurer une précision ou une puissance adéquate dans l’analyse.

retour en haut | page précédente | page suivante

.