Forces des liaisons ioniques et covalentes - Introduction à la chimie

Objectifs d’apprentissage
Résistance de la liaison : Liaisons covalentes
EXEMPLE
Résistance des liaisons ioniques et énergie de maille
EXEMPLE
ACQUISITION CLÉS
FIN DU CHAPITRE EXERCICES
Notes de bas de page
Glossaire
I

Objectifs d’apprentissage

Décrire l’énergétique des liaisons covalentes et ioniques. et ionique
Utiliser les énergies moyennes des liaisons covalentes pour estimer les enthalpies de réaction

La force d’une liaison décrit la force avec laquelle chaque atome est relié à un autre atome, et donc la quantité d’énergie nécessaire pour rompre la liaison entre les deux atomes.

Il est essentiel de se rappeler que de l’énergie doit être ajoutée pour rompre les liaisons chimiques (un processus endothermique), alors que la formation de liaisons chimiques libère de l’énergie (un processus exothermique). Dans le cas de $\text{H}_2$ , la liaison covalente est très forte ; une grande quantité d’énergie, 436 kJ, doit être ajoutée pour briser les liaisons dans une mole de molécules d’hydrogène et provoquer la séparation des atomes:

$\text{H}_2 (g) \longrightarrow \ \text{2H} (g) \\N- \N- \N- \N- \N- \N- énergie de liaison = 436 kJ}$

A l’inverse, la même quantité d’énergie est libérée lorsqu’une mole de $\text{H}_2$ molécules se forme à partir de deux moles d’atomes de H:

$\text{2H} (g) \\N- Flèche courte \N- \N- \N- \N- H}_2(g) \N- \N- \N- \N- \N- \N- énergie de liaison = -436 kJ}$

Résistance de la liaison : Liaisons covalentes

Les molécules stables existent parce que les liaisons covalentes maintiennent les atomes ensemble. On mesure la force d’une liaison covalente par l’énergie nécessaire pour la rompre, c’est-à-dire l’énergie nécessaire pour séparer les atomes liés. La séparation de toute paire d’atomes liés nécessite de l’énergie. Plus une liaison est forte, plus l’énergie nécessaire pour la rompre est importante.

L’énergie nécessaire pour rompre une liaison covalente spécifique dans une mole de molécules gazeuses est appelée énergie de liaison ou énergie de dissociation de la liaison. L’énergie de liaison pour une molécule diatomique, $\text{D}_\text{X-Y}$ , est définie comme le changement d’enthalpie standard pour la réaction endothermique :

$\text{XY} (g) \longarrow \text{X} (g) \text{ + Y} (g) \\N- \N- \N- \N-\N-\N-\N-\N-\N-\N-\N-\N-\N-\N-\N-\N-\N- (D) = \Delta H^{\circuit}$

Par exemple, l’énergie de liaison de la liaison covalente pure H-H, $\text{D}_\text{H-H}$ , est de 436 kJ par mole de liaisons H-H rompues:

$\text{H}_2 (g) \longrightarrow \text{2H} (g) \ \ \ \ \c. (g) \\N- \N- \N- \N- \N- \N- \N- \N- \N- \N- \N- \N- \N- H-H} = \N- delta H^{\circ} = \N-\N- 436 kJ}$

Les molécules comportant trois atomes ou plus ont deux liaisons ou plus. La somme de toutes les énergies de liaison dans une telle molécule est égale à la variation d’enthalpie standard pour la réaction endothermique qui rompt toutes les liaisons de la molécule. Par exemple, la somme des quatre énergies de liaison C-H dans $\text{CH}_4$ , 1660 kJ, est égale au changement d’enthalpie standard de la réaction :

Une réaction est représentée avec des structures de Lewis. La première structure montre un atome de carbone lié de façon simple à quatre atomes d'hydrogène avec le symbole,

L’énergie moyenne de la liaison C-H, $\text{D}_\text{C-H}.$ , est de 1660/4 = 415 kJ/mol car il y a quatre moles de liaisons C-H rompues par mole de la réaction. Bien que les quatre liaisons C-H soient équivalentes dans la molécule d’origine, elles ne nécessitent pas toutes la même énergie pour être rompues ; une fois la première liaison rompue (qui nécessite 439 kJ/mol), les autres liaisons sont plus faciles à rompre. La valeur de 415 kJ/mol est la moyenne, et non la valeur exacte requise pour rompre une quelconque liaison.

La force d’une liaison entre deux atomes augmente lorsque le nombre de paires d’électrons dans la liaison augmente. En général, lorsque la force de la liaison augmente, la longueur de la liaison diminue. Ainsi, on constate que les liaisons triples sont plus fortes et plus courtes que les liaisons doubles entre les deux mêmes atomes ; de même, les liaisons doubles sont plus fortes et plus courtes que les liaisons simples entre les deux mêmes atomes. Les énergies moyennes des liaisons pour certaines liaisons courantes figurent dans le tableau ci-dessous, et une comparaison des longueurs et des forces des liaisons pour certaines liaisons courantes figure dans le tableau suivant. Lorsqu’un atome se lie à divers atomes d’un groupe, la force de la liaison diminue généralement à mesure que l’on descend dans le groupe. Par exemple, $\text{C-F}$ est de 439 kJ/mol, $\text{C-Cl}$ est de 330 kJ/mol, et $\text{C-Br}$ est de 275 kJ/mol.

Énergies de liaison (kJ/mol)
Liaison	Énergie de liaison	Liaison	Énergie de liaison	Liaison	Énergie de liaison
$\text{H-H}$	436	$\text{C-S}$	260	$\text{F-Cl}$	255
$\text{H-C}$	415	$\text{C-Cl}$	330	$\text{F-Br}$	235
$\text{H-N}$	390	$\text{C-Br}$	275	$\text{Si-Si}$	230
$\text{H-O}$	464	$\text{C-I}$	240	$\text{Si-P}$	215
$\text{H-F}$	569	$\text{N-N}$	160	$\text{Si-S}$	225
$\text{H-Si}$	395	$\text{N=N}$	418	$\text{Si-Cl}$	359
$\text{H-P}$	320	$\text{N} {\equiv} \text{N}$	946	$\text{Si-Br}$	290
$\text{H-S}$	340	$\text{N-O}$	200	$\text{Si-I}$	215
$\text{H-Cl}$	432	$\text{N-F}$	270	$\text{P-P}$	215
$\text{H-Br}$	370	$\text{N-P}$	210	$\text{P-S}$	230
$\text{H-I}$	295	$\text{N-Cl}$	200	$\text{P-Cl}$	330
$\text{C-C}$	345	$\text{N-Br}$	245	$\text{P-Br}$	270
$\text{C=C}$	611	$\text{O-O}$	140	$\text{P-I}$	215
$\text{C} {\equiv} \text{C}$	837	$\text{O=O}$	498	$\text{S-S}$	215
$\text{C-N}$	290	$\text{O-F}$	160	$\text{S-Cl}$	250
$\text{C=N}$	615	$\text{O-Si}$	370	$\text{S-Br}$	215
$\text{C} {\equiv} \text{N}$	891	$\text{O-P}$	350	$\text{Cl-Cl}$	243
$\text{C-O}$	350	$\text{O-Cl}$	205	$\text{Cl-Br}$	220
$\text{C=O}$	741	$\text{O-I}$	200	$\text{Cl-I}$	210
$\text{C} {\equiv} \text{O}$	1080	$\text{F-F}$	160	$\text{Br-Br}$	190
$\text{C-F}$	439	$\text{F-Si}$	540	$\text{Br-I}$	180
$\text{C-Si}$	360	$\text{F-P}$	489	$\text{I-I}$	150
$\text{C-P}$	265	$\text{F-S}$	285

Longueurs et énergies moyennes des liaisons pour quelques. liaisons courantes
La liaison	La longueur de la liaison (Å)	L’énergie de la liaison (kJ/mol)
$\text{C-C}$	1,54	345
$\text{C=C}$	1.34	611
$\text{C} {\equiv} \text{C}$	1,20	837
$\text{C-N}$	1,43	290
$\text{C=N}$	1.38	615
$\text{C} {\equiv} \text{N}$	1.16	891
$\text{C-O}$	1,43	350
$\text{C=O}$	1.23	741
$\text{C} \equiv \text{O}$	1,13	1080

L’énergie de liaison est la différence entre le minimum d’énergie (qui se produit à la distance de la liaison) et l’énergie des deux atomes séparés. C’est la quantité d’énergie libérée lors de la formation de la liaison. Inversement, la même quantité d’énergie est nécessaire pour rompre la liaison. Pour la molécule $\text{H}_2$ présentée dans le tableau ci-dessus, à la distance de liaison de 74 pm, le système a une énergie inférieure de 7,24 × 10-19 J à celle des deux atomes d’hydrogène séparés. Ce chiffre peut sembler faible. Cependant, comme nous l’apprendrons plus en détail par la suite, les énergies de liaison sont souvent discutées sur une base par mole. Par exemple, il faut 7,24 × 10-19 J pour briser une liaison H-H, mais il faut 4,36 × 105 J pour briser 1 mole de liaisons H-H. Une comparaison de certaines longueurs et énergies de liaison est présentée dans les tableaux ci-dessus. Nous pouvons trouver un grand nombre de ces liaisons dans une variété de molécules, et ce tableau fournit des valeurs moyennes. Par exemple, la rupture de la première liaison C-H dans $\text{CH}_4$ nécessite 439,3 kJ/mol, tandis que la rupture de la première liaison C-H dans $\text{H-CH}_2\text{C}_6\text{H}_5$ (un diluant à peinture commun) nécessite 375.5 kJ/mol.

Comme on le voit dans les tableaux ci-dessus, une liaison simple carbone-carbone moyenne est de 347 kJ/mol, tandis que dans une liaison double carbone-carbone, la liaison $\pi$ augmente la force de liaison de 267 kJ/mol. L’ajout d’une liaison supplémentaire $\pi$ entraîne une augmentation supplémentaire de 225 kJ/mol. Nous pouvons observer un schéma similaire lorsque nous comparons d’autres liaisons $\sigma$ et $\pi$ . Ainsi, chaque liaison individuelle $\pi$ est généralement plus faible qu’une liaison $\sigma$ correspondante entre les deux mêmes atomes. Dans une liaison $\pi$ , il y a un plus grand degré de chevauchement orbital que dans une liaison $\pi$ .

Nous pouvons utiliser les énergies de liaison pour calculer les changements approximatifs d’enthalpie pour les réactions où les enthalpies de formation ne sont pas disponibles. Les calculs de ce type nous permettront également de savoir si une réaction est exothermique ou endothermique. Une réaction exothermique (ΔH négatif, chaleur produite) se produit lorsque les liaisons des produits sont plus fortes que celles des réactifs. Une réaction endothermique (ΔH positif, chaleur absorbée) résulte lorsque les liaisons dans les produits sont plus faibles que celles dans les réactifs.

Le changement d’enthalpie, ΔH, pour une réaction chimique est approximativement égal à la somme de l’énergie requise pour briser toutes les liaisons dans les réactifs (énergie « in », signe positif) plus l’énergie libérée lorsque toutes les liaisons sont formées dans les produits (énergie « out », signe négatif). Ceci peut être exprimé mathématiquement de la manière suivante :

$\Delta H= \Sigma \text{D}_\text{liaisons brisées}- \Sigma \text{D}_\text{liaisons formées}.$

Dans cette expression, le symbole $\Sigma$ signifie « la somme de » et D représente l’énergie de liaison en kilojoules par mole, qui est toujours un nombre positif. L’énergie de liaison est obtenue à partir d’une table et dépendra du fait que la liaison particulière est une liaison simple, double ou triple. Ainsi, en calculant les enthalpies de cette manière, il est important de prendre en compte la liaison dans tous les réactifs et produits. Comme les valeurs de D sont généralement des moyennes pour un type de liaison dans de nombreuses molécules différentes, ce calcul fournit une estimation approximative, et non une valeur exacte, de l’enthalpie de réaction.

Considérez la réaction suivante :

$\text{H}_2 (g) + \text{Cl}_2 (g) \longrightarrow \text{2HCl}. (g)$

$\text{H-H}} (g) + \text{Cl-Cl} (g) Flèche droite \text{2H-Cl} (g)$

Pour former deux moles de $\text{HCl}$ , il faut rompre une mole de liaisons H-H et une mole de liaisons Cl-Cl. L’énergie nécessaire à la rupture de ces liaisons est la somme de l’énergie de liaison de la liaison H-H (436 kJ/mol) et de la liaison Cl-Cl (243 kJ/mol). Au cours de la réaction, deux moles de liaisons H-Cl sont formées (énergie de liaison = 432 kJ/mol), libérant 2 × 432 kJ ; soit 864 kJ. Comme les liaisons des produits sont plus fortes que celles des réactifs, la réaction libère plus d’énergie qu’elle n’en consomme :

$\Delta H$	$=Sigma \text{D}_\text{bonds broken} - \Sigma \text{D}_\text{bonds formed}$
$\Delta H$	$= - \text{2D}_\text{H-Cl}$
	$= - 2(432) = \text{-185 kJ}$

Cet excès d’énergie est libéré sous forme de chaleur, la réaction est donc exothermique. L’annexe G donne une valeur pour l’enthalpie molaire standard de formation de $\text{HCl}. (g)$ , $\Delta H_\text{f}^{\circ}$ , de -92,307 kJ/mol. Le double de cette valeur est de -184,6 kJ, ce qui concorde bien avec la réponse obtenue précédemment pour la formation de deux moles de HCl.

EXEMPLE

Utilisation des énergies de liaison pour calculer les changements d’enthalpie approximatifs
Le méthanol, $\text{CH}_3\text{OH}.$ , pourrait constituer un excellent carburant alternatif. La réaction à haute température de la vapeur et du carbone produit un mélange de gaz de monoxyde de carbone, $\text{CO}$ , et d’hydrogène, $\text{H}_2$ , à partir duquel on peut produire du méthanol. En utilisant les énergies de liaison dans les tableaux ci-dessus, calculez le changement approximatif d’enthalpie, ΔH, pour la réaction ici :

$\text{CO} (g) + \text{2H}_2 (g) \longrightarrow \text{CH}_3\text{OH} (g)$

Solution
D’abord, nous devons écrire les structures de Lewis des réactifs et des produits :

Un ensemble de diagrammes de Lewis montre une réaction chimique. La première structure montre un atome de carbone avec une paire d'électrons solitaire triple liée à un oxygène avec une paire d'électrons solitaire. À droite de cette structure se trouve un signe plus, puis le chiffre 2 suivi d'un atome d'hydrogène lié à un atome d'hydrogène. À droite de cette structure se trouve une flèche orientée vers la droite, suivie d'un atome d'hydrogène lié à un atome de carbone qui est lié à deux atomes d'hydrogène et à un atome d'oxygène avec deux paires d'électrons solitaires. L'atome d'oxygène est également lié par une liaison simple à un atome d'hydrogène.

À partir de là, nous voyons que ΔH pour cette réaction implique l’énergie requise pour briser une triple liaison C-O et deux liaisons simples H-H, ainsi que l’énergie produite par la formation de trois liaisons simples C-H, d’une liaison simple C-O et d’une liaison simple O-H. On peut l’exprimer comme suit :

$\Delta H =$	$\Sigma \text{D}_\text{bonds broken} -$
$\Delta H =$

En utilisant les valeurs d’énergie de liaison du tableau, nous obtenons :

$\Delta H$
	$= \text{-107 kJ}$

Nous pouvons comparer cette valeur à celle calculée à partir des données $\Delta H_\text{f}^{\circ}$ de l’annexe G :

$\Delta H$

	$= \text{-90.5 kJ}$

Notez qu’il y a un écart assez important entre les valeurs calculées par les deux méthodes différentes. Cela se produit parce que les valeurs D sont la moyenne de différentes forces de liaison ; par conséquent, elles ne donnent souvent qu’un accord approximatif avec d’autres données.

Vérifiez votre apprentissage
L’alcool éthylique, $\text{CH}_3\text{CH}_2\text{OH}.$ , a été l’un des premiers produits chimiques organiques délibérément synthétisés par l’homme. Il a de nombreux usages dans l’industrie, et c’est l’alcool contenu dans les boissons alcoolisées. Il peut être obtenu par la fermentation du sucre ou synthétisé par l’hydratation de l’éthylène dans la réaction suivante :

Un ensemble de structures de Lewis montre une réaction chimique. La première structure montre deux atomes de carbone qui sont doublement liés entre eux et qui sont chacun liés par une liaison simple à deux atomes d'hydrogène. Cette structure est suivie d'un signe plus, puis d'un atome d'oxygène avec deux paires d'électrons solitaires liés de manière simple à deux atomes d'hydrogène. Une flèche orientée vers la droite conduit à un atome de carbone lié par une liaison simple à trois atomes d'hydrogène et à un deuxième atome de carbone. Le deuxième atome de carbone est lié par une liaison simple à deux atomes d'hydrogène et à un atome d'oxygène avec deux paires d'électrons solitaires. L'atome d'oxygène est également lié de façon simple à un atome d'hydrogène.

En utilisant les énergies de liaison dans le tableau, calculez un changement d’enthalpie approximatif, ΔH, pour cette réaction.

Réponse:
-35 kJ

Résistance des liaisons ioniques et énergie de maille

Un composé ionique est stable en raison de l’attraction électrostatique entre ses ions positifs et négatifs. L’énergie de maille d’un composé est une mesure de la force de cette attraction. L’énergie de réseau (ΔHlattice) d’un composé ionique est définie comme l’énergie nécessaire pour séparer une mole du solide en ses ions gazeux constitutifs. Pour le solide ionique MX, l’énergie de réseau est le changement d’enthalpie du processus :

$\text{MX} (s) \longrightarrow \text{M}^{n+} (g) + \text{X}^{n-} (g) \\N\N\N\N\N\N\N\N\N- Delta H_\text{lattice}$

Notez que nous utilisons la convention où le solide ionique est séparé en ions, donc nos énergies de réseau seront endothermiques (valeurs positives). Certains textes utilisent la convention équivalente mais opposée, définissant l’énergie de réseau comme l’énergie libérée lorsque des ions séparés se combinent pour former un réseau et donnant des valeurs négatives (exothermiques). Par conséquent, si vous recherchez les énergies de réseau dans une autre référence, assurez-vous de vérifier quelle définition est utilisée. Dans les deux cas, une magnitude plus élevée pour l’énergie de réseau indique un composé ionique plus stable. Pour le chlorure de sodium, $\Delta H_\text{lattice} = \text{769 kJ}$ . Ainsi, il faut 769 kJ pour séparer une mole de $\text{NaCl} solide.$ en ions gazeux $\text{Na}^+$ et $\text{Cl}^-$ . Lorsqu’une mole de chacun des ions $\text{Na}^+$ gazeux et $\text{Cl}^-$ solides forment $\text{NaCl}$ , 769 kJ de chaleur sont libérés.
L’énergie de réseau $\Delta H_\text{lattice}$ d’un cristal ionique peut être exprimée par l’équation suivante (dérivée de la loi de Coulomb, régissant les forces entre les charges électriques) :

$\Delta H_\text{lattice} = \frac{ \text{C(Z}^+\text{)(Z}^-) }{ \text{R}_\circ }$

dans laquelle C est une constante qui dépend du type de structure cristalline ; Z+ et Z- sont les charges des ions ; et Ro est la distance interionique (la somme des rayons des ions positifs et négatifs). Ainsi, l’énergie de réseau d’un cristal ionique augmente rapidement lorsque les charges des ions augmentent et que la taille des ions diminue. Lorsque tous les autres paramètres sont maintenus constants, le fait de doubler la charge du cation et de l’anion quadruple l’énergie de maille. Par exemple, l’énergie de maille de $\text{LiF}$ (Z+ et Z- = 1) est de 1023 kJ/mol, alors que celle de $\text{MgO}$ (Z+ et Z- = 2) est de 3900 kJ/mol (Ro est presque le même – environ 200 pm pour les deux composés).
Des distances interatomiques différentes produisent des énergies de réseau différentes. Par exemple, nous pouvons comparer l’énergie de maille de $\text{MgF}_2$ (2957 kJ/mol) à celle de $\text{MgI}_2$ (2327 kJ/mol) pour observer l’effet sur l’énergie de maille de la plus petite taille ionique de F- par rapport à I-.

EXEMPLE

Comparaisons d’énergie de réseau
Le rubis, pierre précieuse, est un oxyde d’aluminium, $\text{Al}_2\text{O}_3$ , contenant des traces de $\text{Cr}^{3+}$ . Le composé $\text{Al}_2\text{Se}_3$ est utilisé dans la fabrication de certains dispositifs semi-conducteurs. Lequel a la plus grande énergie de maille, $\text{Al}_2\text{O}_3$ ou $\text{Al}_2\text{Se}_3$ ?

Solution
Dans ces deux composés ioniques, les charges Z+ et Z- sont les mêmes, donc la différence d’énergie de maille dépendra de Ro. L’ion $\text{O}^{2-}$ est plus petit que l’ion $\text{Se}^{2-}$ . Ainsi, $\text{Al}_2\text{O}_3$ aurait une distance interionique plus courte que $\text{Al}_2\text{Se}_3$ , et $\text{Al}_2\text{O}_3$ aurait la plus grande énergie de maille.
Vérifiez vos connaissances
L’oxyde de zinc, $\text{ZnO}$ , est un écran solaire très efficace. Comment l’énergie de la maille de $\text{ZnO}$ par rapport à celle de $\text{NaCl}$ ?

Réponse:
$\text{ZnO}$ aurait la plus grande énergie de maille car les valeurs Z du cation et de l’anion dans $\text{ZnO}$ sont plus grandes, et la distance interionique de $\text{ZnO}$ est plus petite que celle de $\text{NaCl}$ .

ACQUISITION CLÉS

La force d’une liaison covalente est mesurée par son énergie de dissociation de liaison, c’est-à-dire la quantité d’énergie nécessaire pour rompre cette liaison particulière dans une mole de molécules. Les liaisons multiples sont plus fortes que les liaisons simples entre les mêmes atomes. L’enthalpie d’une réaction peut être estimée en fonction de l’apport d’énergie nécessaire à la rupture des liaisons et de l’énergie libérée lors de la formation de nouvelles liaisons. Pour les liaisons ioniques, l’énergie de maille est l’énergie nécessaire pour séparer une mole d’un composé en ses ions en phase gazeuse. L’énergie de maille augmente pour les ions ayant des charges plus élevées et des distances plus courtes entre les ions.

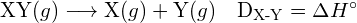
Energie de liaison pour une molécule diatomique : $\text{XY} (g) \longrightarrow \text{X} (g) + \text{Y} (g) \\N- \N- \N- \N- \N- \N- \N --- = \N- \N- \N --- Delta H^{\circuit}$
Changement enthalpique : $\Delta H = \Sigma \text{D}_\text{\i} liaisons brisées} - \Sigma \text{D}_\i{\i} liaisons formées}$
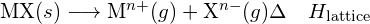
L’énergie de réseau pour un solide MX : $\text{MX} (s) \longrightarrow \text{M}^{n+} (g) + \text{X}^{n-} (g) \Delta \ \\N H_\text{{\i}lattice}$
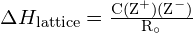
L’énergie de réseau pour un cristal ionique : $\Delta H_\text{lattice} = \frac{ \text{C(Z}^+\text{)(Z}^-) }{ \text{R}_\circ }$

FIN DU CHAPITRE EXERCICES

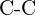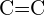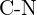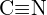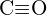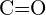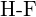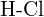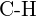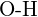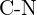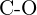
Quelle liaison dans chacune des paires de liaisons suivantes est la plus forte ? (a) $\text{C-C}$ ou $\text{C=C}$ (b) $\text{C-N}$ ou $\text{C} {\equiv} \text{N}$ (c) $\text{C} {\equiv} \text{O}$ ou $\text{C=O}$ (d) $\text{H-F}$ ou $\text{H-Cl}$ (e) $\text{C-H}$ ou $\text{O-H}$ (f) $\text{C-N}$ ou $\text{C-O}$
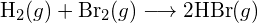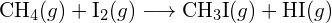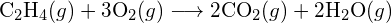En utilisant les énergies de liaison dans le tableau, déterminez le changement approximatif d’enthalpie pour chacune des réactions suivantes : (a) $\text{H}_2 (g) + \text{Br}_2 (g) \longrightarrow \text{2HBr} (g)$ (b) $\text{CH}_4 (g) + \text{I}_2(g) \longrightarrow \text{CH}_3\text{I} (g) + \text{HI} (g)$ (c) $\text{C}_2\text{H}_4 (g) + \text{3O}_2 (g) \longrow \text{2CO}_2 (g) + \text{2H}_2\text{O} (g)$
(a) -114 kJ ; (b) 30 kJ ; (c) -1055 kJ
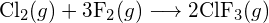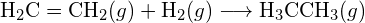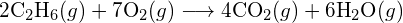
En utilisant les énergies de liaison dans le tableau, déterminez le changement approximatif d’enthalpie pour chacune des réactions suivantes : (a) $\text{Cl}_2 (g) + \text{3F}_2 (g) \longrightarrow \text{2ClF}_3 (g)$ (b) $\text{H}_2\text{C} = \text{CH}_2 (g) + \text{H}_2 (g) \Flèche droite \text{H}_3\text{CCH}_3 (g)$ (c) $\text{2C}_2\text{H}_6 (g) + \text{7O}_2 (g) \longueur droite \text{4CO}_2 (g) + \text{6H}_2\text{O} (g)$
Dessinez une courbe qui décrit l’énergie d’un système avec des atomes de H et de Cl à des distances variables. Ensuite, trouvez l’énergie minimale de cette courbe de deux façons.(a) Utilisez l’énergie de liaison trouvée dans les tableaux pour calculer l’énergie d’une seule 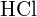$\text{HCl}.$ liaison (Indice : combien de liaisons y a-t-il dans une mole ?)(b) Utilisez l’enthalpie de réaction et les énergies de liaison pour H2 et Cl2 pour résoudre l’énergie d’une mole de 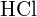$\text{HCl}$ liaisons.
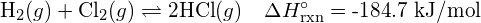
$\text{H}_2 (g) + \text{Cl}_2 (g) \rightleftharpoons \text{2HCl} (g) \N- \N- \N- Kelta H_\N}^{\circ} = \N--184.7 kJ/mol}$

Expliquez pourquoi les liaisons se produisent à des distances de liaison moyennes spécifiques au lieu que les atomes se rapprochent infiniment les uns des autres.

La distance de liaison moyenne spécifique est la distance avec l’énergie la plus faible. À des distances inférieures à la distance de liaison, les charges positives des deux noyaux se repoussent et l’énergie globale augmente.
Lorsqu’une molécule peut former deux structures différentes, la structure avec les liaisons les plus fortes est généralement la forme la plus stable. Utilisez les énergies de liaison pour prédire la structure correcte de la molécule d’hydroxylamine:
La plus grande énergie de liaison se trouve dans la figure de gauche. C’est la forme la plus stable.
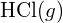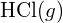Comment l’énergie de liaison de $\text{HCl} (g)$ diffère de l’enthalpie standard de formation de $\text{HCl}. (g)$ ?
En utilisant les données d’enthalpie standard de formation de l’annexe G, montrez comment l’enthalpie standard de formation de 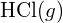$\text{HCl} (g)$ peut être utilisée pour déterminer l’énergie de liaison.

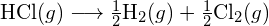
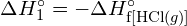
$\text{HCl} (g) \longrightarrow \frac{1}{2}\text{H}_2 (g) + \frac{1}{2}\text{Cl}_2 (g)$ $\Delta H_1^{\circ} = -\Delta H_{\text{f}^{\circ}$

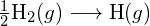
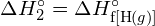
$\frac{1}{2}\text{H}_2 (g) \longuante \text{H}} (g)$ $\Delta H_2^{\circ} = \Delta H_{\text{f}^{\circ}$

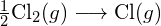
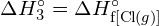
$\frac{1}{2}\text{Cl}_2 (g) \longarrow \text{Cl}_2 (g) (g)$ $\Delta H_3^{\circ} = \Delta H_{\text{f}^{\circ}$

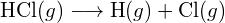
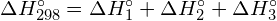
$\text{HCl} (g) + \Longueur-flèche \N- H. (g) + \text{Cl} (g)$ $\Delta H_{298}^{\circ} = \Delta H_1^{\circ} + \Delta H_2^{\circ} + \Delta H_3^{\circ}$

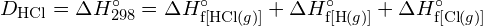
$D_\text{HCl} = \Delta H_{298}^{\circ} = \Delta H_{\text{f}^{\circ} + \Delta H_{\text{f}^{\circ} + \Delta H_{\text{f}^{\circ}$

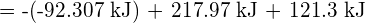
$\text{= -(-92.307 kJ) + 217.97 kJ + 121.3 kJ}$
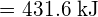
$\text{= 431.6 kJ}$
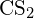En utilisant les données d’enthalpie de formation standard de l’annexe G, calculez l’énergie de liaison de la double liaison carbone-soufre dans $\text{CS}_2$ .
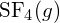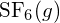En utilisant les données d’enthalpie standard de formation de l’annexe G, déterminez quelle liaison est plus forte : la liaison S-F dans $\text{SF}_4 (g)$ ou dans $\text{SF}_6 (g)$ ?
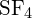La liaison S-F dans $\text{SF}_4$ est plus forte.
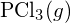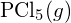En utilisant les données d’enthalpie de formation standard de l’annexe G, déterminer quelle liaison est plus forte : la liaison P-Cl dans $\text{PCl}_3 (g)$ ou dans $\text{PCl}_5 (g)$ ?
Complétez la structure de Lewis suivante en ajoutant des liaisons (et non des atomes), puis indiquez la liaison la plus longue:

Les liaisons simples C-C sont les plus longues.
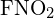Utilisez l’énergie de liaison pour calculer une valeur approximative de ΔH pour la réaction suivante. Quelle est la forme la plus stable de $\text{FNO}_2$ ?
Utilisez les principes de la structure atomique pour répondre à chacune des questions suivantes :1 (a) Le rayon de l’atome de Ca est de 197 pm ; le rayon de l’ion 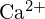$\text{Ca}^{2+}$ est de 99 pm. Expliquez la différence. (b) L’énergie de maille de 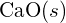$\text{CaO} (s)$ est de -3460 kJ/mol ; l’énergie de maille de 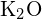$\text{K}_2\text{O}$ est de -2240 kJ/mol. Expliquez la différence. (c) Compte tenu de ces valeurs d’ionisation, expliquez la différence entre Ca et K en ce qui concerne leur première et deuxième énergie d’ionisation.

.

Elément Première énergie d’ionisation (kJ/mol) Deuxième énergie d’ionisation (kJ/mol)

K 419 3050

Ca 590 1140

(d) La première énergie d’ionisation de Mg est de 738 kJ/mol et celle de Al de 578 kJ/mol. Expliquez cette différence.

(a) Lorsque deux électrons sont retirés de la coquille de valence, le rayon du Ca perd le niveau d’énergie le plus externe et revient au niveau inférieur n = 3, dont le rayon est beaucoup plus petit.(b) La charge +2 du calcium tire l’oxygène beaucoup plus près par rapport au K, ce qui augmente l’énergie du réseau par rapport à un ion moins chargé.

(c) L’enlèvement de l’électron 4s dans Ca nécessite plus d’énergie que l’enlèvement de l’électron 4s dans K à cause de l’attraction plus forte du noyau et de l’énergie supplémentaire nécessaire pour briser l’appariement des électrons. La deuxième énergie d’ionisation pour K exige qu’un électron soit retiré d’un niveau d’énergie inférieur, où l’attraction du noyau est beaucoup plus forte pour l’électron. De plus, de l’énergie est nécessaire pour désapparier deux électrons dans une orbitale complète. Pour Ca, le second potentiel d’ionisation nécessite de retirer seulement un électron solitaire dans le niveau d’énergie extérieur exposé.

(d) Dans Al, l’électron retiré est relativement non protégé et non apparié dans une orbitale p. L’énergie plus élevée pour Mg reflète principalement le désappairage de l’électron 2s.
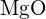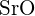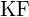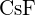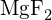Pour laquelle des substances suivantes l’énergie requise pour convertir une mole du solide en ions séparés est-elle la plus faible ? (a) $\text{MgO}$ (b) $\text{SrO}$ (c) $\text{KF}$ (d) $\text{CsF}$ (e) $\text{MgF}_2$
(d)
La réaction d’un métal, 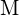$\text{M}$ , avec un halogène, 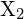$\text{X}_2$ , se déroule par une réaction exothermique comme indiqué par cette équation : 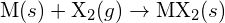$\text{M} (s) + \text{X}_2 (g) \rightarrow \text{MX}_2 (s)$ . Pour chacun des cas suivants, indiquez quelle option rendra la réaction plus exothermique. Expliquez vos réponses. (a) un grand rayon par rapport à un petit rayon pour 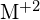$\text{M}^{+2}$ (b) une énergie d’ionisation élevée vs. une énergie d’ionisation faible pour 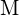$\text{M}$ (c) une énergie de liaison croissante pour l’halogène (d) une affinité électronique décroissante pour l’halogène (e) une taille croissante de l’anion formé par l’halogène
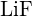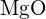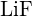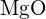L’énergie de réseau de $\text{LiF}.$ est de 1023 kJ/mol, et la distance Li-F est de 201 pm. $\text{MgO}$ cristallise dans la même structure que $\text{LiF}$ mais avec une distance Mg-O de 205 pm. Laquelle des valeurs suivantes se rapproche le plus de l’énergie de réseau de $\text{MgO}$ : 256 kJ/mol, 512 kJ/mol, 1023 kJ/mol, 2046 kJ/mol, ou 4008 kJ/mol ? Expliquez votre choix.
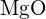4008 kJ/mol ; les deux ions dans $\text{MgO}$ ont deux fois la charge des ions dans 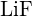$\text{LiF}$ ; la longueur de la liaison est très similaire et les deux ont la même structure ; on s’attend à un quadruplement de l’énergie d’après l’équation de l’énergie de maille
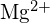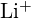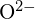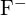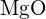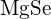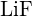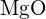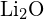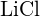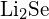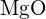
Quel composé dans chacune des paires suivantes a la plus grande énergie de maille ? Remarque : $\text{Mg}^{2+}$ et $\text{Li}^+$ ont des rayons similaires ; $\text{O}^{2-}$ et $\text{F}^-$ ont des rayons similaires. Expliquez vos choix. (a) $\text{MgO}$ ou $\text{MgSe}$ (b) $\text{LiF}$ ou $\text{MgO}$ (c) $\text{Li}_2\text{O}$ ou $\text{LiCl}$ (d) $\text{Li}_2\text{Se}$ ou $\text{MgO}$
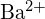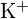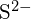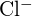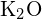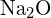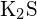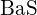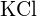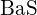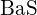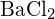Quel composé dans chacune des paires suivantes a la plus grande énergie de réseau ? Remarque : $\text{Ba}^{2+}$ et $\text{K}^+$ ont des rayons similaires ; $\text{S}^{2-}$ et $\text{Cl}^-$ ont des rayons similaires. Expliquez vos choix. (a) $\text{K}_2\text{O}$ ou $\text{Na}_2\text{O}$ (b) $\text{K}_2\text{S}$ ou $\text{BaS}$ (c) $\text{KCl}$ ou $\text{BaS}$ (d) $\text{BaS}$ ou $\text{BaCl}_2$
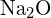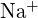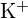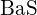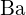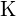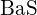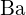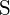(a) $\text{Na}_2\text{O}$ ; $\text{Na}^+$ a un rayon plus petit que $\text{K}^+$ ; (b) $\text{BaS}$ ; $\text{Ba}$ a une charge plus grande que $\text{K}$ ; (c) $\text{BaS}$ ; $\text{Ba}$ et $\text{S}$ ont des charges plus importantes ; (d) 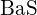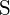$\text{BaS}$ ; $\text{S}$ a une plus grande charge
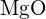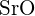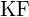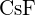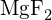
Quel est le composé suivant qui nécessite le plus d’énergie pour convertir une mole du solide en ions séparés ? (a) $\text{MgO}$ (b) $\text{SrO}$ (c) $\text{KF}$ (d) $\text{CsF}$ (e) $\text{MgF}_2$
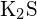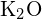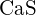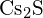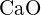Lequel des composés suivants nécessite le plus d’énergie pour convertir une mole du solide en ions séparés ? (a) $\text{K}_2\text{S}$ (b) $\text{K}_2\text{O}$ (c) $\text{CaS}$ (d) $\text{Cs}_2\text{S}$ (e) $\text{CaO}$
(e)

Elément	Première énergie d’ionisation (kJ/mol)	Deuxième énergie d’ionisation (kJ/mol)
K	419	3050
Ca	590	1140

Notes de bas de page

1 Cette question est tirée de l’examen de placement avancé en chimie et est utilisée avec la permission de l’Educational Testing Service.

Glossaire

énergie de liaison (aussi, énergie de dissociation des liaisons) énergie nécessaire pour rompre une liaison covalente dans une substance gazeuse énergie de réseau (ΔHréseau) énergie nécessaire pour séparer une mole d’un solide ionique en ses composants. ions gazeux

énergie nécessaire pour séparer une mole d’un solide ionique en ses composants ions gazeux

Chimie introductive

Objectifs d’apprentissage

Résistance de la liaison : Liaisons covalentes

EXEMPLE

Résistance des liaisons ioniques et énergie de maille

EXEMPLE

ACQUISITION CLÉS

FIN DU CHAPITRE EXERCICES

Notes de bas de page

Glossaire

I

Laisser un commentaire Annuler la réponse