Description simple
Envisageons d’abord la liaison pi dans l’éthène du point de vue de la théorie MO simplifiée (dans cet exemple, nous ne tiendrons pas compte des liaisons sigma dans la molécule, et nous ne penserons qu’à la liaison π). Nous commençons avec deux orbitales atomiques : une orbitale 2p non hybridée de chaque carbone. Chacune contient un électron unique. Dans la théorie MO, les deux orbitales atomiques se combinent mathématiquement pour former deux orbitales moléculaires pi, une orbitale pi de liaison de faible énergie et une orbitale pi* antibonding de haute énergie.

Orbitales moléculaires de l’éthène (éthylène)
Dans l’orbitale pi de liaison, les deux lobes ombrés des orbitales p interagissent de manière constructive l’un avec l’autre, tout comme les deux lobes non ombrés (rappelez-vous, le choix arbitraire de l’ombrage représente les signes mathématiques (+) et (-) pour la fonction d’onde mathématique décrivant l’orbitale). Il y a une densité accrue d’électrons entre les deux noyaux de carbone dans l’orbitale moléculaire – c’est une interaction de liaison.
Dans l’orbitale pi* antiliaison de plus haute énergie, le lobe ombré d’une orbitale p interagit de manière destructive avec le lobe non ombré de la seconde orbitale p, ce qui conduit à un nœud entre les deux noyaux et à une répulsion globale entre les noyaux de carbone.
En utilisant à nouveau le principe de « construction », nous plaçons les deux électrons dans l’orbitale moléculaire pi de liaison, de plus faible énergie. L’orbitale pi* antiliante reste vide.
Description MO plus détaillée de l’éthène
La théorie des orbitales moléculaires a été appliquée avec beaucoup de succès aux grands systèmes conjugués, en particulier ceux contenant des chaînes d’atomes de carbone avec des liaisons simples et doubles alternées. Une approximation introduite par Hückel en 1931 ne considère que les électrons p délocalisés se déplaçant dans un cadre de liaisons \pi -. Il s’agit, en fait, d’une version plus sophistiquée d’un modèle à électrons libres. Pour un cours d’introduction à la chimie organique, nous n’avons pas besoin d’utiliser toutes les mathématiques de Hückel, mais pour ceux qui aiment approfondir, une analyse plus détaillée est donnée ici.
L’hydrocarbure le plus simple à considérer qui présente des liaisons \pi est l’éthène (éthylène), qui est composé de quatre atomes d’hydrogène et de deux atomes de carbone. Expérimentalement, nous savons que les angles H-C-H et H-C-C de l’éthène sont d’environ 120°. Cet angle suggère que les atomes de carbone sont hybridés sp2, ce qui signifie qu’une orbitale sp2 singulièrement occupée sur un carbone chevauche une orbitale s singulièrement occupée sur chaque H et un lobe sp2 singulièrement occupé sur l’autre C. Ainsi, chaque carbone forme un ensemble de trois liaisons σ : deux C-H (sp2 + s) et un C-C (sp2 + sp2) (partie (a) de la figure 13.1. ci-dessous).

Figure 13.1. (a) Le cadre à liaison σ est formé par le chevauchement de deux ensembles d’orbitales hybrides sp2 de carbone singulièrement occupées et de quatre orbitales 1s d’hydrogène singulièrement occupées pour former des liaisons par paire d’électrons. Ceci utilise 10 des 12 électrons de valence pour former un total de cinq liaisons σ (quatre liaisons C-H et une liaison C-C). (b) Une orbitale 2pz non hybridée et occupée de façon unique reste sur chaque atome de carbone pour former une liaison π carbone-carbone. (Note : par convention, dans les molécules planes, l’axe perpendiculaire au plan moléculaire est l’axe z.)
L’approximation de Hückel est utilisée pour déterminer les énergies et les formes des orbitales moléculaires \pi dans les systèmes conjugués. Dans le cadre de l’approximation de Hückel, la liaison covalente dans ces hydrocarbures peut être séparée en deux « cadres » indépendants : le cadre de liaison \sigma – et le cadre de liaison \sigma -. Les fonctions d’onde utilisées pour décrire les orbitales de liaison dans chaque cadre résultent de différentes combinaisons d’orbitales atomiques. La méthode se limite à traiter les hydrocarbures conjugués et, en particulier, seules les orbitales moléculaires à électrons \pi sont incluses car elles déterminent les propriétés générales de ces molécules ; les électrons sigma sont ignorés. C’est ce qu’on appelle la séparabilité sigma-pi et elle est justifiée par l’orthogonalité des orbitales \sigma et \pi dans les molécules planes. Pour cette raison, la méthode de Hückel est limitée aux systèmes planaires. L’approximation de Hückel suppose que les électrons dans les liaisons \pi « ressentent » un potentiel électrostatique dû à l’ensemble du cadre de liaison \sigma dans la molécule (c’est-à-dire qu’elle se concentre uniquement sur la formation des liaisons \pi, étant donné que le cadre de liaison \sigma a déjà été formé).
Systèmes conjugués
Un système conjugué possède une région de p-orbitales chevauchantes, pontant les liaisons simples interjacentes, qui permettent une délocalisation des électrons \pi à travers toutes les p-orbitales alignées adjacentes. Ces électrons \pi n’appartiennent pas à une seule liaison ou à un seul atome, mais plutôt à un groupe d’atomes.
Ethène
Avant de considérer le traitement de Hückel pour l’éthène, il est bénéfique de revoir l’image générale de liaison de la molécule. La liaison dans l’éthène implique l’hybridation sp^2 des orbitales atomiques 2s , 2p_x , et 2p_y sur chaque atome de carbone ; laissant les orbitales 2p_z intactes (figure 13.2).
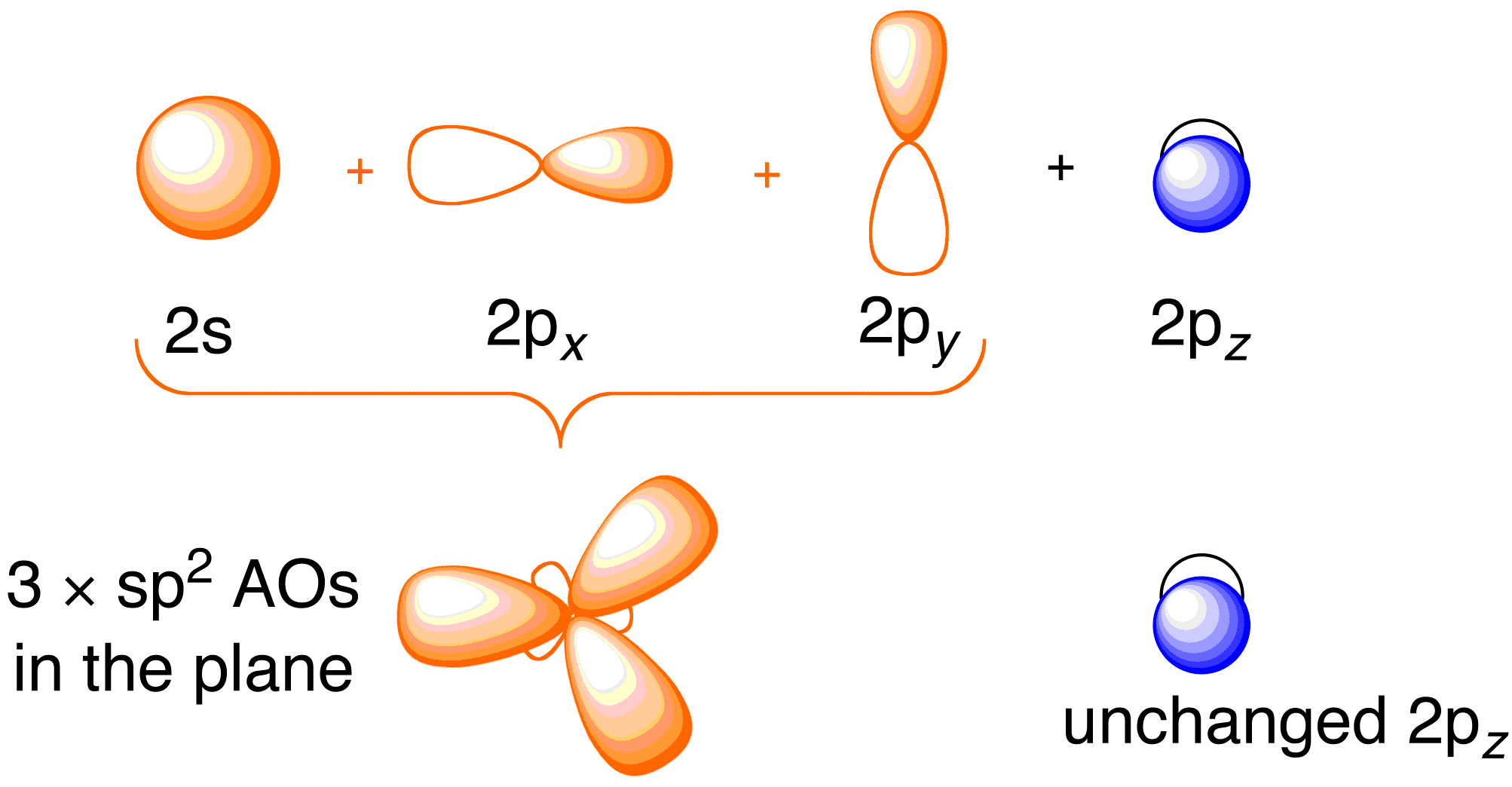
Figure 13.2. Hybridation des orbitales atomiques du carbone pour donner des orbitales hybrides sp^2 pour la liaison aux atomes d’hydrogène dans l’éthène. Image utilisée avec la permission de ChemTube (CC-SA-BY-NC ; Nick Greeves).
L’utilisation des orbitales hybrides dans l’approche des orbitales moléculaires décrite ici est simplement une commodité et n’invoque pas la théorie de la liaison de valence (directement). Une description identique peut être extraite en utilisant exclusivement des orbitales atomiques sur le carbone, mais l’interprétation des fonctions d’onde résultantes est moins intuitive. Par exemple, la ième orbitale moléculaire peut être décrite via des orbitales hybrides
\
ou via des orbitales atomiques.
\
où \{a_i\} et \{c_i\} sont des coefficients de l’expansion. L’une ou l’autre description fonctionnera et les deux approches sont identiques puisque
où \{c_i\} sont des coefficients décrivant l’orbitale hybridée.
La liaison se produit via le mélange des électrons dans les orbitales hybrides sp^2 sur le carbone et les électrons dans les orbitales atomiques 1s des quatre atomes d’hydrogène (figure 13.2. ci-dessus à gauche), ce qui donne le cadre de liaison \sigma -. La structure de liaison \pi résulte des orbitales 2p_z non hybridées (Figure 13.2. ci-dessus, à droite). L’indépendance de ces deux cadres est démontrée dans le diagramme d’orbitales moléculaires qui en résulte dans la figure ci-dessous ; la théorie de Hückel ne s’intéresse qu’à la description des orbitales moléculaires et des énergies du cadre de liaison \pi.

Figure 13.3 : Orbitales moléculaires démontrant la séparabilité sigma-pi du cadre de liaison \pi – (bleu) et des cadres de liaison \sigma – (rouge) de l’éthylène.
Le traitement de Hückel s’attache uniquement à décrire les orbitales moléculaires et les énergies du cadre de liaison \pi.
Puisque la théorie de Hückel est une considération spéciale de la théorie des orbitales moléculaires, les orbitales moléculaires | \psi_i \rangle peuvent être décrites comme une combinaison linéaire des orbitales atomiques 2p_z \phi au carbone avec leurs coefficients \{c_i\} correspondants :
\
Pour l’analyse complète de la chimie quantique utilisant l’équation de Schrödinger (non requise pour le cours de chimie organique), voir cette page Libretexts.
Ces orbitales moléculaires forment le cadre de liaison π et puisque chaque carbone contribue un électron à ce cadre, seule l’orbitale moléculaire la plus basse ( | \psi_1 \rangle ) est occupée (figure ) dans l’état fondamental. La configuration électronique correspondante est alors \pi_1^2 .

Figure 13.4 : Représentation schématique du cadre des orbitales moléculaires \pi pour l’éthylène . Remarquez que l’orbitale moléculaire antiliante a un nœud de plus que l’orbitale moléculaire liante, comme prévu puisqu’elle a une énergie plus élevée.
HOMO et LUMO sont des acronymes pour l’orbitale moléculaire la plus occupée et l’orbitale moléculaire inoccupée la plus basse, respectivement, et sont souvent appelées orbitales frontières. La différence d’énergie entre l’HOMO et la LUMO est appelée la lacune HOMO-LUMO.
Les orbitales moléculaires \pi calculées en 3-D sont présentées dans la figure 13.5.

Figure 13.5 : Orbitales moléculaires \pi calculées pour l’éthylène . (gauche) l’orbitale liante (ψ1) et (droite) l’orbitale antiliante (ψ2).
Contributeurs
- Seymour Blinder (professeur émérite de chimie et de physique à l’université du Michigan, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
.
