Dans une distribution normale, les données sont distribuées symétriquement et sans biais. Lorsqu’elles sont tracées sur un graphique, les données suivent une forme de cloche, la plupart des valeurs se regroupant autour d’une région centrale et s’amenuisant à mesure qu’elles s’éloignent du centre.
Les distributions normales sont également appelées distributions gaussiennes ou courbes en cloche en raison de leur forme.

- Pourquoi les distributions normales sont-elles importantes ?
- Quelles sont les propriétés des distributions normales ?
- Quel est votre score de plagiat ?
- Règle empirique
- Théorème de la limite centrale
- Formule de la courbe normale
- Qu’est-ce que la distribution normale standard ?
- Détermination de la probabilité en utilisant la distribution z
- Questions fréquemment posées sur les distributions normales
Pourquoi les distributions normales sont-elles importantes ?
Toutes sortes de variables dans les sciences naturelles et sociales sont normalement ou approximativement normalement distribuées. La taille, le poids à la naissance, la capacité de lecture, la satisfaction au travail ou les résultats au SAT ne sont que quelques exemples de ces variables.
Parce que les variables normalement distribuées sont si courantes, de nombreux tests statistiques sont conçus pour des populations normalement distribuées.
Comprendre les propriétés des distributions normales signifie que vous pouvez utiliser les statistiques inférentielles pour comparer différents groupes et faire des estimations sur des populations en utilisant des échantillons.
Quelles sont les propriétés des distributions normales ?
Les distributions normales ont des caractéristiques clés qui sont faciles à repérer dans les graphiques :
- La moyenne, la médiane et le mode sont exactement les mêmes.
- La distribution est symétrique par rapport à la moyenne – la moitié des valeurs tombent sous la moyenne et l’autre moitié au-dessus de la moyenne.
- La distribution peut être décrite par deux valeurs : la moyenne et l’écart-type.


La moyenne est le paramètre de localisation tandis que l’écart type est le paramètre d’échelle.
La moyenne détermine où le pic de la courbe est centré. L’augmentation de la moyenne déplace la courbe vers la droite, tandis que sa diminution déplace la courbe vers la gauche.


L’écart-type étire ou comprime la courbe. Un petit écart-type entraîne une courbe étroite, tandis qu’un grand écart-type entraîne une courbe large.


Règle empirique
La règle empirique, ou la règle du 68-95-99.7, vous indique où se situent la plupart de vos valeurs dans une distribution normale :
- Environ 68% des valeurs se situent à 1 écart-type de la moyenne.
- Environ 95% des valeurs se situent à 2 écarts-type de la moyenne.
- Environ 99,7% des valeurs se situent à 3 écarts-type de la moyenne.
Suivant la règle empirique :
- Environ 68% des scores sont compris entre 1000 et 1300, 1 écart-type au-dessus et au-dessous de la moyenne.
- Environ 95% des scores sont compris entre 850 et 1450, 2 écarts types au-dessus et au-dessous de la moyenne.
- Environ 99,7% des scores sont compris entre 700 et 1600, 3 écarts types au-dessus et au-dessous de la moyenne.


La règle empirique est un moyen rapide d’avoir une vue d’ensemble de vos données et de vérifier s’il y a des valeurs aberrantes ou extrêmes qui ne suivent pas ce modèle.
Si les données provenant de petits échantillons ne suivent pas de près ce modèle, alors d’autres distributions comme la distribution t peuvent être plus appropriées. Une fois que vous avez identifié la distribution de votre variable, vous pouvez appliquer les tests statistiques appropriés.
Théorème de la limite centrale
Le théorème de la limite centrale est la base du fonctionnement des distributions normales en statistique.
En recherche, pour avoir une bonne idée de la moyenne d’une population, l’idéal serait de collecter des données à partir de plusieurs échantillons aléatoires au sein de la population. Une distribution d’échantillonnage de la moyenne est la distribution des moyennes de ces différents échantillons.
Le théorème de la limite centrale montre ce qui suit :
- La loi des grands nombres : Lorsque vous augmentez la taille de l’échantillon (ou le nombre d’échantillons), alors la moyenne de l’échantillon se rapprochera de la moyenne de la population.
- Avec de grands échantillons multiples, la distribution d’échantillonnage de la moyenne est normalement distribuée, même si votre variable originale n’est pas normalement distribuée.
Les tests statistiques paramétriques supposent généralement que les échantillons proviennent de populations normalement distribuées, mais le théorème de la limite centrale signifie que cette hypothèse n’est pas nécessaire à satisfaire lorsque vous avez un échantillon suffisamment grand.
Vous pouvez utiliser des tests paramétriques pour de grands échantillons provenant de populations avec n’importe quel type de distribution, tant que d’autres hypothèses importantes sont satisfaites. Un échantillon de 30 personnes ou plus est généralement considéré comme grand.
Pour les petits échantillons, l’hypothèse de normalité est importante car la distribution d’échantillonnage de la moyenne n’est pas connue. Pour obtenir des résultats précis, vous devez être sûr que la population est normalement distribuée avant de pouvoir utiliser des tests paramétriques avec de petits échantillons.
Formule de la courbe normale
Une fois que vous avez la moyenne et l’écart-type d’une distribution normale, vous pouvez ajuster une courbe normale à vos données en utilisant une fonction de densité de probabilité.


Dans une fonction de densité de probabilité, l’aire sous la courbe vous indique la probabilité. La distribution normale est une distribution de probabilité, donc l’aire totale sous la courbe est toujours 1 ou 100 %.
La formule de la fonction de densité de probabilité normale semble assez compliquée. Mais pour l’utiliser, il suffit de connaître la moyenne et l’écart-type de la population.
Pour toute valeur de x, vous pouvez brancher la moyenne et l’écart-type dans la formule pour trouver la densité de probabilité de la variable prenant cette valeur de x.
| Formule de densité de probabilité normale | Explication |
|---|---|
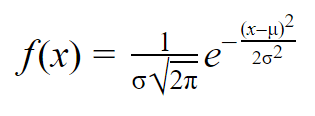 |
|
Sur votre graphique de la fonction de densité de probabilité, la probabilité est la zone ombrée sous la courbe qui se trouve à droite de l’endroit où vos résultats du SAT sont égaux à 1380.


Vous pouvez trouver la valeur de probabilité de ce score en utilisant la distribution normale standard.
Qu’est-ce que la distribution normale standard ?
La distribution normale standard, aussi appelée la distribution z, est une distribution normale spéciale où la moyenne est 0 et l’écart-type est 1.
Toute distribution normale est une version de la distribution normale standard qui a été étirée ou comprimée et déplacée horizontalement à droite ou à gauche.


Alors que les observations individuelles des distributions normales sont désignées par x, elles sont désignées par z dans la distribution z. Chaque distribution normale peut être convertie en distribution normale standard en transformant les valeurs individuelles en z-scores.
Les z-scores vous indiquent combien d’écarts types de la moyenne chaque valeur se situe.


Il suffit de connaître la moyenne et l’écart-type de votre distribution pour trouver le z-score d’une valeur.
| Formule du score Z | Explication |
|---|---|
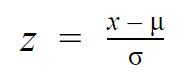 |
|
Nous convertissons les distributions normales en distribution normale standard pour plusieurs raisons :
- Pour trouver la probabilité que les observations d’une distribution soient supérieures ou inférieures à une valeur donnée.
- Pour trouver la probabilité qu’une moyenne d’échantillon diffère significativement d’une moyenne de population connue.
- Pour comparer les scores sur différentes distributions avec différentes moyennes et écarts types.
Détermination de la probabilité en utilisant la distribution z
Chaque score z est associé à une probabilité, ou valeur p, qui vous indique la probabilité que des valeurs inférieures à ce score z se produisent. Si vous convertissez une valeur individuelle en un score z, vous pouvez alors trouver la probabilité que toutes les valeurs jusqu’à cette valeur se produisent dans une distribution normale.
La moyenne de notre distribution est de 1150, et l’écart-type est de 150. Le score z vous indique combien d’écarts types séparent 1380 de la moyenne.
| Formule | Calcul |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
Pour un score z de 1,53, la valeur p est de 0,937. C’est la probabilité que les scores SAT soient de 1380 ou moins (93,7 %), et c’est l’aire sous la courbe à gauche de la zone ombrée.


Pour trouver la zone ombrée, vous enlevez 0.937 de 1, qui est l’aire totale sous la courbe.
Probabilité de x>1380 = 1 – 0,937 = 0,063
Cela signifie qu’il est probable que seulement 6,3 % des scores au SAT dans votre échantillon dépassent 1380.
Questions fréquemment posées sur les distributions normales
Dans une distribution normale, les données sont distribuées de manière symétrique et sans asymétrie. La plupart des valeurs se regroupent autour d’une région centrale, les valeurs s’amenuisant à mesure qu’elles s’éloignent du centre.
Les mesures de tendance centrale (moyenne, mode et médiane) sont exactement les mêmes dans une distribution normale.
La distribution normale standard, aussi appelée distribution z, est une distribution normale spéciale où la moyenne est 0 et l’écart-type est 1.
Toute distribution normale peut être convertie en distribution normale standard en transformant les valeurs individuelles en z-scores. Dans une distribution z, les z-scores vous indiquent combien d’écarts types de la moyenne chaque valeur se situe.
La règle empirique, ou règle des 68-95-99,7, vous indique où se situent la plupart des valeurs dans une distribution normale :
- Environ 68% des valeurs se situent à 1 écart-type de la moyenne.
- Environ 95% des valeurs se situent à 2 écarts-types de la moyenne.
- Environ 99,7 % des valeurs se situent à l’intérieur de 3 écarts types de la moyenne.
La règle empirique est un moyen rapide d’avoir une vue d’ensemble de vos données et de vérifier si des valeurs aberrantes ou extrêmes ne suivent pas ce modèle.
La distribution t est une façon de décrire un ensemble d’observations où la plupart des observations tombent près de la moyenne, et le reste des observations constitue les queues de chaque côté. C’est un type de distribution normale utilisé pour les échantillons de petite taille, lorsque la variance des données est inconnue.
La distribution t forme une courbe en cloche lorsqu’elle est tracée sur un graphique. Elle peut être décrite mathématiquement à l’aide de la moyenne et de l’écart-type.

