Un triangle avec un angle droit s’appelle un triangle droit. Le côté opposé à l’angle droit s’appelle l’hypoténuse du triangle. Les deux autres côtés sont appelés jambages. Les deux autres angles n’ont pas de nom particulier, mais ils sont toujours complémentaires. Vous comprenez pourquoi ? La somme totale des angles d’un triangle est de 180 degrés, et l’angle droit est de 90 degrés, donc les deux autres doivent avoir une somme de 90 degrés.
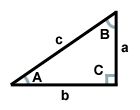
Le triangle ci-dessus a pour côté c son hypoténuse, pour côtés a et b ses jambes, et pour angle C son angle droit. Les angles A etB sont complémentaires.
Il y a deux types de triangles droits que tout mathématicien doit très bien connaître. L’un est le triangle rectangle formé lorsqu’une altitude est tirée d’un sommet d’un triangle équilatéral, formant deux triangles rectangles congruents. Les angles du triangle seront de 30, 60 et 90 degrés, ce qui donne au triangle son nom : triangle 30-60-90. Le rapport des longueurs des côtés dans de tels triangles est toujours le même : si la branche opposée à l’angle de 30 degrés est de longueur x, la branche opposée à l’angle de 60 degrés sera de x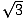
, et l’hypoténuse en face de l’angle droit sera de 2x. Voici un triangle 30-60-90 représenté ci-dessous.
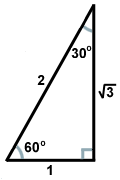
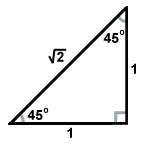
L’autre triangle rectangle commun résulte de la paire de triangles créée lorsqu’une diagonale divise un carré en deux triangles. Chacun de ces triangles est congruent, et possède des angles de mesures 45, 45 et 90 degrés. Si les branches opposées aux angles de 45 degrés sont de longueur x, l’hypoténuse a une longueur de x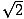
. Ce rapport est valable pour tous les triangles 45-45-90. Les triangles 45-45-90 sont aussi souvent appelés triangles droits isocèles.
Une dernière caractéristique à noter est que les jambes d’un triangle rectangle sont aussi des altitudes du triangle. Par conséquent, l’aire d’un triangle rectangle est la moitié du produit des longueurs de ses jambes.