A normális eloszlásban az adatok szimmetrikusan, ferdeség nélkül oszlanak el. Grafikonon ábrázolva az adatok harang alakúak, a legtöbb érték egy központi régió körül csoportosul, és a középponttól távolodva csökken.
A normális eloszlást alakja miatt Gauss-eloszlásnak vagy haranggörbének is nevezik.

Miért fontosak a normál eloszlások?
A természet- és társadalomtudományokban mindenféle változó normál vagy közelítőleg normál eloszlású. A magasság, a születési súly, az olvasási képesség, a munkahelyi elégedettség vagy a SAT pontszámok csak néhány példa az ilyen változókra.
Miatt a normális eloszlású változók olyan gyakoriak, számos statisztikai tesztet normális eloszlású populációkra terveztek.
A normális eloszlások tulajdonságainak ismerete azt jelenti, hogy a következtetési statisztikát különböző csoportok összehasonlítására és populációkra vonatkozó becslések készítésére használhatja a minták segítségével.
Melyek a normális eloszlások tulajdonságai?
A normális eloszlásoknak vannak olyan kulcsfontosságú jellemzői, amelyek könnyen észrevehetők a grafikonokon:
- A középérték, a medián és a módusz pontosan megegyezik.
- Az eloszlás az átlag körül szimmetrikus – az értékek fele az átlag alá, fele az átlag fölé esik.
- Az eloszlás két értékkel írható le: az átlag és a szórás.


Az átlag az elhelyezkedési paraméter, míg a szórás a skálaparaméter.
Az átlag határozza meg, hol van a görbe csúcsának középpontja. Az átlag növelésével a görbe jobbra, míg csökkentésével balra tolódik.


A szórás megnyújtja vagy összenyomja a görbét. Egy kis szórás keskeny görbét eredményez, míg egy nagy szórás széles görbéhez vezet.


Empirikus szabály
Az empirikus szabály, vagy a 68-95-99.7 szabály, megmondja, hogy egy normális eloszlásban az értékek többsége hol helyezkedik el:
- Az értékek mintegy 68%-a az átlagtól 1 szóráson belül van.
- Az értékek mintegy 95%-a az átlagtól 2 szóráson belül van.
- Az értékek mintegy 99,7%-a az átlagtól 3 szóráson belül van.
Az empirikus szabály követése:
- A pontszámok mintegy 68%-a 1000 és 1300 között van, 1 szórással az átlag felett és alatt.
- A pontszámok mintegy 95%-a 850 és 1450 között van, 2 standard eltéréssel az átlag felett és alatt.
- A pontszámok mintegy 99,7%-a 700 és 1600 között van, 3 standard eltéréssel az átlag felett és alatt.


Az empirikus szabály egy gyors módja annak, hogy áttekintést kapjon az adatokról, és ellenőrizze, hogy vannak-e olyan kiugró vagy szélsőértékek, amelyek nem ezt a mintát követik.
Ha a kis mintákból származó adatok nem követik szorosan ezt a mintát, akkor más eloszlások, például a t-eloszlás megfelelőbb lehet. Miután azonosította a változó eloszlását, megfelelő statisztikai teszteket alkalmazhat.
Központi határértéktétel
A központi határértéktétel az alapja annak, hogy a normális eloszlások hogyan működnek a statisztikában.
A kutatásban ahhoz, hogy jó képet kapjunk a populáció átlagáról, ideális esetben a populáción belül több véletlenszerű mintából gyűjtünk adatokat. Az átlag mintavételes eloszlása ezen különböző minták átlagainak eloszlása.
A központi határértéktétel a következőket mutatja:
- A nagy számok törvénye: Ahogy növeljük a mintanagyságot (vagy a minták számát), úgy közelít a minta átlaga a populáció átlagához.
- Több nagy minta esetén az átlag mintavételi eloszlása normális eloszlású, még akkor is, ha az eredeti változó nem normális eloszlású.
A parametrikus statisztikai tesztek általában feltételezik, hogy a minták normális eloszlású populációkból származnak, de a központi határértéktétel azt jelenti, hogy ennek a feltételezésnek nem szükséges megfelelni, ha elég nagy mintával rendelkezünk.
A parametrikus teszteket bármilyen eloszlású populációkból származó nagy mintákra használhatjuk, amennyiben más fontos feltételezések teljesülnek. A 30 vagy annál nagyobb mintanagyság általában nagynak számít.
A kis minták esetében a normalitás feltételezése azért fontos, mert az átlag mintavételi eloszlása nem ismert. A pontos eredmények érdekében biztosnak kell lennie abban, hogy a sokaság normális eloszlású, mielőtt kis minták esetén parametrikus teszteket alkalmazhatna.
A normális görbe formulája
Ha már megvan a normális eloszlás átlaga és szórása, akkor a valószínűségi sűrűségfüggvény segítségével normális görbét illeszthet az adatokhoz.


A valószínűségi sűrűségfüggvényben a görbe alatti terület mondja meg a valószínűséget. A normális eloszlás valószínűségi eloszlás, ezért a görbe alatti teljes terület mindig 1 vagy 100%.
A normális valószínűségi sűrűségfüggvény képlete meglehetősen bonyolultnak tűnik. Használatához azonban csak a populáció átlagát és szórását kell ismerned.
Az x bármelyik értékére az átlagot és a szórást beillesztheted a képletbe, hogy megtaláld a változó valószínűségi sűrűségét, amely az x adott értékét veszi fel.
| Normális valószínűségi sűrűségképlet | Magyarázat |
|---|---|
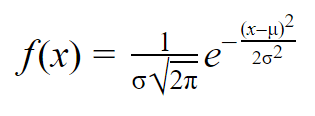 |
|
A valószínűségi sűrűségfüggvény grafikonján a valószínűség az a görbe alatti árnyékolt terület, amely attól a pontszámtól jobbra fekszik, ahol a SAT pontszámok megegyeznek az 1380-zal.


Ezeknek a pontszámoknak a valószínűségi értékét a standard normáleloszlás segítségével találhatod meg.
Mi a standard normáleloszlás?
A standard normális eloszlás, más néven z-eloszlás, egy speciális normális eloszlás, ahol az átlag 0, a szórás pedig 1.
Minden normális eloszlás a standard normális eloszlás egy olyan változata, amelyet megnyújtottak vagy összenyomtak, és vízszintesen jobbra vagy balra toltak.


Míg a normális eloszlások egyes megfigyeléseit x-nek nevezzük, addig a z-eloszlásban z-nek. Minden normális eloszlás átalakítható a standard normális eloszlássá, ha az egyes értékeket z-értékekké alakítjuk.
A z-értékek megmondják, hogy az egyes értékek hány standard eltéréssel térnek el az átlagtól.


Egy érték z-pontszámának kiszámításához csak az eloszlás átlagát és szórását kell ismerned.
| Z-score képlet | Magyarázat |
|---|---|
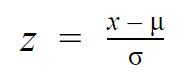 |
|
A normális eloszlásokat több okból alakítjuk át a standard normális eloszlásra:
- Hogy megtaláljuk annak a valószínűségét, hogy egy eloszlásban a megfigyelések egy adott érték fölé vagy alá esnek.
- Hogy megtaláljuk annak a valószínűségét, hogy egy minta átlaga jelentősen eltér egy ismert populációs átlagtól.
- A különböző átlagokkal és szórással rendelkező eloszlásokon kapott pontszámok összehasonlításához.
Valószínűség megállapítása a z-eloszlás segítségével
Minden z-értékhez tartozik egy valószínűség, vagy p-érték, amely megmondja, hogy milyen valószínűséggel fordulnak elő az adott z-érték alatti értékek. Ha egy egyedi értéket z-pontszámmá alakítunk át, akkor meg tudjuk találni az összes értéknek az adott értékig való előfordulási valószínűségét egy normális eloszlásban.
Az eloszlásunk átlaga 1150, a szórás pedig 150. A z-pontszám megmondja, hogy hány szórásnyira van 1380 az átlagtól.
| Forma | Kiszámítás |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
1,53-as z-pontszám esetén a p-érték 0,937. Ez annak a valószínűsége, hogy az SAT pontszám 1380 vagy annál kevesebb (93,7%), és ez a görbe alatti terület az árnyékolt terület bal oldalán.


Az árnyékolt terület megtalálásához el kell vonni 0.937-et 1-ből, ami a görbe alatti teljes terület.
Az x valószínűsége>1380 = 1 – 0,937 = 0,063
Ez azt jelenti, hogy valószínű, hogy a mintában csak a SAT pontszámok 6,3%-a haladja meg az 1380 pontot.
Gyakori kérdések a normális eloszlásról
A normális eloszlásban az adatok szimmetrikus eloszlásúak, ferdeség nélkül. A legtöbb érték egy központi régió köré csoportosul, és az értékek a középponttól távolodva csökkennek.
A központi tendencia mértékegységei (átlag, módusz és medián) pontosan megegyeznek a normális eloszlásban.
A standard normális eloszlás, más néven z-eloszlás, egy speciális normális eloszlás, ahol az átlag 0, a szórás pedig 1.
Minden normális eloszlás átalakítható standard normális eloszlássá, ha az egyes értékeket z-értékekké alakítjuk. A z-eloszlásban a z-pontszámok megmondják, hogy az egyes értékek hány szórásnyira vannak az átlagtól.
Az empirikus szabály vagy a 68-95-99,7 szabály megmondja, hogy egy normális eloszlásban az értékek többsége hol helyezkedik el:
- Az értékek körülbelül 68%-a az átlagtól 1 szóráson belül van.
- Az értékek körülbelül 95%-a az átlagtól 2 szóráson belül van.
- Az értékek mintegy 99,7%-a az átlag 3 szórásán belül van.
Az empirikus szabály egy gyors módja annak, hogy áttekintést kapjunk az adatokról, és ellenőrizzük a kiugró vagy szélsőséges értékeket, amelyek nem ezt a mintát követik.
A t-eloszlás a megfigyelések olyan halmazának leírására szolgál, ahol a legtöbb megfigyelés az átlag közelébe esik, a többi megfigyelés pedig a kétoldali csóvákat alkotja. Ez a normáleloszlás egyik típusa, amelyet kisebb mintanagyságok esetén használnak, ahol az adatok szórása ismeretlen.
A t-eloszlás egy grafikonon ábrázolva haranggörbét alkot. Matematikailag az átlag és a szórás segítségével írható le.

