Logisztikus regresszióelemzés

A logisztikus regresszióelemzés kimenetelét gyakran 0 vagy 1 értékkel kódolják, ahol az 1 azt jelzi, hogy az érdekes kimenetel jelen van, a 0 pedig azt, hogy az érdekes kimenetel nincs jelen. Ha p-t annak valószínűségeként határozzuk meg, hogy a kimenet 1, akkor a többszörös logisztikus regressziós modell a következőképpen írható fel:

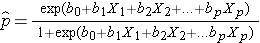
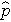a kimenet jelenlétének várható valószínűsége; X1-től Xp-ig a különböző független változók; és b0-tól bp-ig a regressziós együtthatók. A többszörös logisztikus regressziós modellt néha másképp írják. A következő formában a kimenetel annak az esélynek a várható logaritmusa, hogy a kimenetel jelen van,

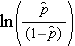
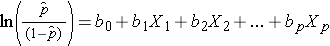
Megjegyezzük, hogy a fenti egyenlet jobb oldala úgy néz ki, mint a többszörös lineáris regressziós egyenlet. A logisztikus regressziós modellben a regressziós együtthatók becslésének technikája azonban eltér a többszörös lineáris regressziós modellben a regressziós együtthatók becsléséhez használt technikától. A logisztikus regresszióban a modellből levezetett együtthatók (pl. b1) a várható logaritmikus esélyek változását jelzik az X1 egy egységnyi változásához képest, minden más prediktort állandónak tartva. Ezért a becsült regressziós együttható antilogikusa, exp(bi), egy esélyhányadost eredményez, amint azt az alábbi példa mutatja.

Példa a logisztikus regresszióra – az elhízás és a CVD közötti kapcsolat

Már korábban elemeztük egy olyan vizsgálat adatait, amelynek célja az elhízás (a BMI > 30) és az incidens szív- és érrendszeri betegségek közötti kapcsolat értékelése volt. Az adatokat olyan résztvevőktől gyűjtöttük, akik 35 és 65 év közöttiek voltak, és a vizsgálat kezdetén nem szenvedtek szív- és érrendszeri betegségben (CVD). Minden résztvevőt 10 éven keresztül követtek a szív- és érrendszeri betegségek kialakulása szempontjából. Az adatok összefoglalása e modul 2. oldalán található. A kiigazítatlan vagy nyers relatív kockázat RR = 1,78, a kiigazítatlan vagy nyers esélyhányados pedig OR = 1,93 volt. Azt is megállapítottuk, hogy az életkor zavaró tényező, és a Cochran-Mantel-Haenszel-módszer alkalmazásával becsültük a kiigazított relatív kockázatot RRCMH =1,44-re és a kiigazított esélyhányadost ORCMH =1,52-re. Most logisztikus regresszióelemzéssel értékeljük az elhízás és az incidens kardiovaszkuláris betegség közötti összefüggést az életkorhoz igazítva.

A logisztikus regresszióelemzés a következőket tárja fel:

Függő változó	Regressziós együttható	Chi-négyzet	P-érték
Intercept	-2.367	307.38	0.0001
elhízás	0.658	9.87	0.0017

Az egyszerű logisztikus regressziós modell az elhízást az incidens CVD log esélyével hozza összefüggésbe:

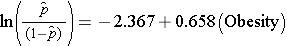
Az elhízás egy indikátor változó a modellben, a következőképpen kódolva: 1=elhízott és 0=nem elhízott. Az incidens CVD logaritmikus esélye 0,658-szor nagyobb az elhízott személyeknél, mint a nem elhízottaknál. Ha a regressziós együttható antilog-ját vesszük, exp(0,658) = 1,93, megkapjuk a nyers vagy kiigazítatlan esélyhányadost. A CVD kialakulásának esélye 1,93-szor nagyobb az elhízott személyek körében a nem elhízott személyekhez képest. Az elhízás és a CVD előfordulása közötti kapcsolat statisztikailag szignifikáns (p=0,0017). Vegyük észre, hogy a logisztikus regresszióelemzésben a regressziós paraméterek szignifikanciájának értékelésére szolgáló tesztstatisztikák a chi-négyzet statisztikán alapulnak, szemben a t-statisztikával, mint a lineáris regresszióelemzés esetében. Ennek az az oka, hogy a regressziós paraméterek becslésére egy másik becslési technikát, az úgynevezett maximális valószínűség becslést használják (technikai részletekért lásd Hosmer és Lemeshow3).

Néhány statisztikai számítási csomag a logisztikus regresszióelemzési eljárás részeként esélyhányadosokat, valamint az esélyhányadosok 95%-os konfidenciaintervallumait is generálja. Ebben a példában az esélyhányados becslése 1,93, a 95%-os konfidenciaintervallum pedig (1,281, 2,913).

Az elhízás és a CVD közötti összefüggés vizsgálatakor korábban megállapítottuk, hogy az életkor zavaró tényező. a következő többszörös logisztikus regressziós modell az elhízás és a CVD incidens közötti összefüggést becsüli meg, az életkorra korrigálva. A modellben ismét két korcsoportot veszünk figyelembe (50 év alattiak és 50 évesek és idősebbek). Az elemzéshez a korcsoportot a következőképpen kódoljuk: 1=50 éves és idősebb, 0=50 évnél fiatalabb.

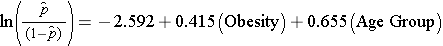
Ha az elhízáshoz kapcsolódó regressziós együttható antilogikusát, exp(0,415) = 1,52-t vesszük, megkapjuk az életkorhoz igazított esélyhányadost. A CVD kialakulásának esélye 1,52-szer nagyobb az elhízott személyek körében a nem elhízott személyekhez képest, az életkorhoz igazítva. A 9.2. szakaszban a Cochran-Mantel-Haenszel-módszert használtuk az életkorral korrigált esélyhányados előállítására, és a következőket találtuk:

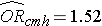
Ez szemlélteti, hogy a többszörös logisztikus regressziós elemzés hogyan használható a zavaró tényezők figyelembevételére. A modellek kiterjeszthetők több zavaró változó egyidejű figyelembevételére. A többszörös logisztikus regresszióelemzés a zavaró tényezők és a hatásmódosítás értékelésére is használható, és a megközelítések megegyeznek a többszörös lineáris regresszióelemzésben használtakkal. A többszörös logisztikus regresszióelemzés arra is használható, hogy megvizsgáljuk több kockázati tényező hatását (szemben az egyetlen kockázati tényezőre való összpontosítással) egy dichotóm kimenetelre.

Példa – Az alacsony csecsemősúlyhoz társuló kockázati tényezők

Tegyük fel, hogy a vizsgálók a terhesség kedvezőtlen kimeneteleivel is foglalkoznak, beleértve a terhességi cukorbetegséget, a preeklampsziát (azaz a terhesség okozta magas vérnyomást) és a koraszülést. Emlékezzünk arra, hogy a vizsgálatban 832 terhes nő vett részt, akik demográfiai és klinikai adatokat szolgáltattak. A vizsgálati mintában 22 (2,7%) nőnél alakul ki preeklampszia, 35 (4,2%) nőnél terhességi cukorbetegség, 40 (4,8%) nőnél pedig koraszülés. Tegyük fel, hogy meg kívánjuk vizsgálni, hogy az anyák életkorával korrigálva vannak-e különbségek az egyes kedvezőtlen terhességi kimenetelekben faji/etnikai hovatartozás szerint. Három külön logisztikus regressziós elemzést végeztünk, amelyek az egyes kimeneteleket külön-külön az anyák faját és az anya életkorát (években kifejezve) tükröző 3 dummy vagy indikátor változóval hozták összefüggésbe. Az eredmények az alábbiakban olvashatók.

eredmény: Pre-eclampsia	Regressziós együttható	Chi-négyzet	P-érték	Odds Ratio (95% CI)
Intercept	-3.066	4.518	0.0335	–
Fekete faj	2.191	12.640	0.0004	8.948 (2.673, 29.949)
Hispanic race	-0.1053	0.0325	0.8570	0.900 (0.286, 2.829)
Más faj	0.0586	0.0021	0.9046	1.060 (0.104, 3.698)
Az anyák életkora (év)	-0.0252	0.3574	0,5500	0,975 (0,898, 1,059)

A preeklampszia egyetlen statisztikailag szignifikáns különbsége a fekete és fehér anyák között van.

A fekete anyáknál közel 9-szer nagyobb a preeklampszia kialakulásának valószínűsége, mint a fehér anyáknál, az anyák életkorával korrigálva. A 95%-os konfidenciaintervallum a preeklampsziás fekete és fehér nők esélyhányadosának összehasonlítására nagyon széles (2,673 és 29,949 között). Ez annak köszönhető, hogy a kimeneti események száma alacsony (a teljes mintában csak 22 nőnél alakul ki preeklampszia) és a fekete bőrű nők kis száma szerepel a vizsgálatban. Így ezt az összefüggést óvatosan kell értelmezni.

Míg az esélyhányados statisztikailag szignifikáns, a konfidenciaintervallum azt sugallja, hogy a hatás nagysága a 2,6-szoros növekedéstől a 29,9-szeres növekedésig terjedhet. Nagyobb vizsgálatra van szükség a hatás pontosabb becsléséhez.

Gesztenciális cukorbetegség	Regressziós együttható	Chi-négyzet	P-érték	Odds Ratio (95% CI)
Intercept	-5.823	22,968	0,0001	–
Fekete faj	1,621	6.660	0.0099	5.056 (1.477, 17.312)
Hispanic race	0.581	1.766	0.1839	1.787 (0.759, 4.207)
Más faj	1.348	5.917	0.0150	3.848 (1.299, 11.395)
Anya kora (év)	0.071	4.314	0.0378	1.073 (1.004, 1.147)

A terhességi cukorbetegség tekintetében statisztikailag szignifikáns különbség van a fekete és fehér anyák között (p=0.0099) és a magukat más fajúnak valló anyák között a fehérhez képest (p=0.0150), az anya korával korrigálva. Az anya életkora szintén statisztikailag szignifikáns (p=0,0378), az idősebb nőknél nagyobb valószínűséggel alakul ki terhességi cukorbetegség, a faji/etnikai hovatartozásra korrigálva.

Eredmény: Koraszülés	Regressziós együttható	Chi-négyzet	P-érték	Odds Ratio (95% CI)
Intercept	-1.443	1.602	0.2056	–
Fekete faj	-0.082	0.015	0.9039	0.921 (0.244, 3.483)
Hispanic race	-1.564	9.497	0.0021	0.209 (0.077, 0.566)
Más faj	0.548	1.124	0.2890	1.730 (0.628,4.767)
Anya kora (év.)	00,037	1,198	0,2737	0,963 (0,901, 1,030)

A terminus előtti szülés tekintetében az egyetlen statisztikailag jelentős különbség a latin és fehér anyák között van (p=0,0021). A spanyolajkú anyáknál 80%-kal kisebb a valószínűsége a koraszülés előtti szülés kialakulásának, mint a fehér anyáknál (esélyhányados = 0,209), az anya életkorával korrigálva.

A többváltozós módszerek számítási szempontból bonyolultak, és általában statisztikai számítási csomag használatát igénylik. A többváltozós módszerek felhasználhatók a zavaró tényezők értékelésére és kiigazítására, annak megállapítására, hogy van-e hatásmódosulás, vagy több expozíció vagy kockázati tényező kimenetelre gyakorolt kapcsolatának egyidejű értékelésére. A többváltozós elemzések összetettek, és mindig úgy kell megtervezni őket, hogy biológiailag plauzibilis összefüggéseket tükrözzenek. Bár viszonylag könnyen figyelembe lehet venni egy további változót egy többszörös lineáris vagy többszörös logisztikus regressziós modellben, csak olyan változókat szabad bevonni, amelyek klinikailag jelentőséggel bírnak.

Nem szabad elfelejteni, hogy a többváltozós modellek csak a vizsgálatban mért zavaró változók közötti különbségeket tudják korrigálni vagy figyelembe venni. Ezenkívül a többváltozós modelleket csak akkor szabad a zavaró tényezők figyelembevételére használni, ha a zavaró tényezők eloszlásában van némi átfedés az egyes kockázati tényezőcsoportok között.

A rétegzett elemzések nagyon informatívak, de ha az egyes rétegek mintái túl kicsik, az elemzésekből hiányozhat a pontosság. A vizsgálatok tervezésekor a vizsgálóknak gondosan oda kell figyelniük a lehetséges hatásmódosítókra. Ha felmerül a gyanú, hogy egy expozíció vagy kockázati tényező közötti összefüggés bizonyos csoportokban eltérő, akkor a vizsgálatot úgy kell megtervezni, hogy az egyes csoportokban elegendő számú résztvevő legyen. Mintavételi méret képleteket kell használni az egyes rétegekben szükséges vizsgálati alanyok számának meghatározásához, hogy az elemzés megfelelő pontosságot vagy teljesítményt biztosítson.

vissza a tetejére | előző oldal | következő oldal