Egyszerű leírás
Lássuk először az etén pi-kötését egy egyszerűsített MO-elmélet szempontjából (ebben a példában nem vesszük figyelembe a molekula szigma-kötéseit, és csak a π-kötésre gondolunk). Két atomi orbitálból indulunk ki: mindkét szénből egy-egy hibridizálatlan 2p orbitál. Mindkettő egy-egy elektront tartalmaz. A MO-elméletben a két atomi matematikailag két pi molekuláris orbitált alkot, egy alacsony energiájú pi kötési orbitált és egy magas energiájú pi* antibonding orbitált.

Etén (etilén)
Molekuláris orbitáljai
A kötő pi-orbitálon a p-orbitálok két árnyékolt nyalábja konstruktív kölcsönhatásban van egymással, akárcsak a két árnyékolatlan nyaláb (ne feledjük, az önkényesen választott árnyékolás a matematikai (+) és (-) jeleket jelenti az orbitált leíró matematikai hullámfüggvényben). A molekuláris orbitálisban a két szénatommag között megnövekedett elektronsűrűség van – ez egy kötési kölcsönhatás.
A magasabb energiájú antibonding pi* orbitálisban az egyik p orbitális árnyékolt nyalábja destruktív kölcsönhatásba lép a második p orbitális árnyékolatlan nyalábjával, ami a két atommag közötti csomóponthoz és a szénatommagok közötti általános taszításhoz vezet.
Az “építkezés” elvét alkalmazva ismét a két elektront az alacsonyabb energiájú, kötő pi molekuláris orbitálba helyezzük. Az antibonding pi* orbitál üresen marad.
Az etén részletesebb MO leírása
A molekuláris orbitálelméletet nagy sikerrel alkalmazták nagy konjugált rendszerekre, különösen azokra, amelyek szénatomláncokat tartalmaznak váltakozó egyszerű és kettős kötésekkel. A Hückel által 1931-ben bevezetett közelítés csak a delokalizált p elektronokat veszi figyelembe, amelyek \pi -kötések keretén belül mozognak. Ez tulajdonképpen a szabadelektronos modell kifinomultabb változata. Egy bevezető szerves kémia kurzuson nem kell Hückel teljes matematikáját használnunk, de azok számára, akik mélyebbre szeretnének ásni, itt részletesebb elemzést adunk.
A legegyszerűbb szénhidrogén, amelyet \pi kötést mutat, az etén (etilén), amely négy hidrogénatomból és két szénatomból áll. Kísérletileg tudjuk, hogy az eténben a H-C-H és H-C-C-C szögek körülbelül 120°-osak. Ez a szög arra utal, hogy a szénatomok sp2-hibridizáltak, ami azt jelenti, hogy egy egyszeresen foglalt sp2-orbitál az egyik szénen átfedésben van egy egyszeresen foglalt s-orbitállal minden H-n és egy egyszeresen foglalt sp2-nyalábbal a másik C-n. Így minden szén három \sigma kötést alkot: két C-H (sp2 + s) és egy C-C (sp2 + sp2) (az alábbi 13.1. ábra (a) része).

13.1. ábra. (a) A σ-kötéses váz a szén két egyedileg foglalt sp2 hibrid pálya és négy egyedileg foglalt hidrogén 1s pálya átfedésével jön létre elektronpáros kötések kialakításával. Ez a 12 valenciaelektronból 10-et használ fel összesen öt σ-kötés (négy C-H-kötés és egy C-C-kötés) kialakításához. (b) Minden szénatomon egy-egy egyszeresen foglalt, nem hibridizált 2pz-orbitális marad, hogy szén-szén π-kötést képezzen. (Megjegyzés: konvenció szerint síkbeli molekulákban a molekulasíkra merőleges tengely a z-tengely.)
A Hückel-közelítést a konjugált rendszerek \pi molekuláris pályáinak energiáinak és alakjának meghatározására használják. A Hückel-közelítésen belül a kovalens kötés ezekben a szénhidrogénekben két független “keretre” osztható: a \sigma -kötési keretre és a \sigma -kötési keretre. Az egyes keretekben a kötési pályák leírására használt hullámfüggvények az atomi pályák különböző kombinációiból adódnak. A módszer a konjugált szénhidrogének kezelésére korlátozódik, és kifejezetten csak a \pi elektron molekuláris pályákat veszi figyelembe, mivel ezek határozzák meg e molekulák általános tulajdonságait; a szigma elektronokat figyelmen kívül hagyja. Ezt sigma-pi szeparálhatóságnak nevezik, és a \sigma és \pi pályák ortogonalitása indokolja a síkbeli molekulákban. Emiatt a Hückel-módszer síkbeli rendszerekre korlátozódik. A Hückel-közelítés feltételezi, hogy az \pi kötésekben lévő elektronok a molekula teljes \sigma -kötési keretének köszönhetően elektrosztatikus potenciált “éreznek” (azaz csak az \pi kötések kialakulására összpontosít, mivel a \sigma kötési keret már kialakult).
Konjugált rendszerek
A konjugált rendszerben a szomszédos egyszerű kötéseket áthidaló, átfedő p-orbitálisok olyan régiója van, amely lehetővé teszi a \pi elektronok delokalizációját az összes szomszédos, egymáshoz igazított p-orbitálison. Ezek az \pi elektronok nem egyetlen kötéshez vagy atomhoz, hanem egy atomcsoporthoz tartoznak.
Etén
Az etén Hückel-féle kezelése előtt hasznos áttekinteni a molekula általános kötésképét. Az eténben a kötés az egyes szénatomok 2s , 2p_x és 2p_y atomi pályáinak sp^2 hibridizációját jelenti; a 2p_z pályákat érintetlenül hagyva (13.2. ábra).
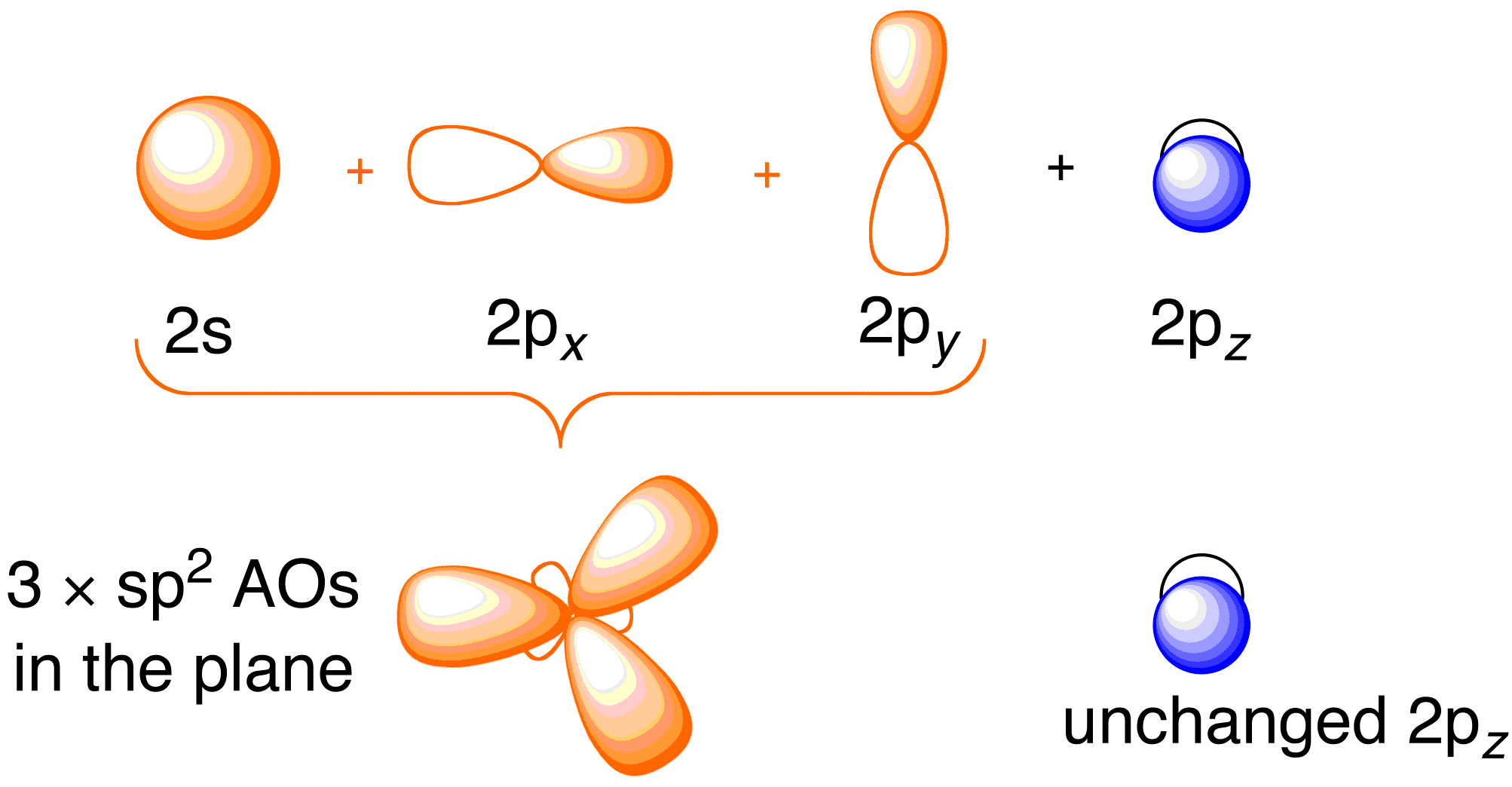
13.2. ábra. A szén atomi pályák hibridizálása, hogy sp^2 hibrid pályákat kapjunk a hidrogénatomokhoz való kötődéshez az eténben. A képet a ChemTube engedélyével használtuk (CC-SA-BY-NC; Nick Greeves).
A hibrid orbitálok használata az itt leírt molekuláris orbitális megközelítésben csupán kényelmi szempont, és nem a valenciakötés-elméletre való (közvetlen) hivatkozás. Azonos leírás nyerhető ki kizárólag atomi pályák felhasználásával a szénre, de a kapott hullámfüggvények értelmezése kevésbé intuitív. Például az i-edik molekuláris orbitál leírható hibrid orbitálokkal
\
vagy atomi orbitálokkal.
\
ahol \{a_i\} és \{c_i\} a kiterjesztés együtthatói. Mindkét leírás működik, és mindkettő azonos megközelítés, mivel
\
ahol \{c_i\} a hibridizált orbitálisokat leíró együtthatók.
A kötés a szén sp^2 hibrid pályáin lévő elektronok és a négy hidrogénatom 1s atomi pályáin lévő elektronok keveredésén keresztül történik (13.2. ábra balra fent), ami a \sigma -kötési keretet eredményezi. A \pi -kötési keret a nem hibridizált 2p_z pályákból adódik (13.2. ábra jobbra fent). E két keretrendszer függetlenségét az alábbi ábrán látható eredő molekuláris pályadiagram mutatja; a Hückel-elmélet csak a \pi kötési keretrendszer molekuláris pályáinak és energiáinak leírásával foglalkozik.

13.3. ábra: Az etilén \pi -kötési keretének (kék) és \sigma -kötési keretének (piros) sigma-pi elválaszthatóságát szemléltető molekuláris pályák.
A Hückel-féle kezelés csak az \pi kötési keret molekuláris pályáinak és energiáinak leírásával foglalkozik.
Mivel a Hückel-elmélet a molekuláris pályaelmélet egy speciális megfontolása, a molekuláris pályák | \psi_i \rendszert a szénnél lévő 2p_z \phi atomi pályák lineáris kombinációjaként írhatjuk le a megfelelő \{c_i\} koefficiensekkel:
\
A teljes kvantumkémiai elemzést a Schrödinger-egyenlet segítségével (a szerves kémia órán nem szükséges) lásd ezen a Libretexts oldalon.
Ezek a molekuláris orbitálok alkotják a π-kötéses keretet, és mivel minden szén egy-egy elektronnal járul hozzá ehhez a kerethez, az alapállapotban csak a legalacsonyabb molekuláris orbitál ( | \psi_1 \rangle ) foglalt (ábra ). A megfelelő elektronkonfiguráció \pi_1^2 .

13.4. ábra: Az etilén \pi molekulapálya-keretének sematikus ábrázolása . Vegyük észre, hogy az antibonding molekuláris orbitálnak eggyel több csomópontja van, mint a bonding molekuláris orbitálnak, ahogy az várható volt, mivel magasabb az energiája.
HOMO és LUMO a legmagasabb elfoglalt molekuláris orbitál, illetve a legalacsonyabb nem elfoglalt molekuláris orbitál rövidítései, és gyakran nevezik őket határorbitáloknak. A HOMO és a LUMO közötti energiakülönbséget HOMO-LUMO résnek nevezzük.
A számított 3-D \pi molekuláris pályák a 13.5. ábrán láthatók.

13.5. ábra: Az etilén számított \pi molekuláris pályái . (balra) a kötési orbitál (ψ1) és (jobbra) az antibonding (ψ2) orbitál.
Munkatársak
- Seymour Blinder (a Michigani Egyetem, Ann Arbor, kémia és fizika professor emeritusa)
- Wikipedia
- StackExchange (Philipp)
