Az egy derékszögű háromszöget derékszögű háromszögnek nevezzük. A derékszöggel szemben lévő oldalt a háromszög hipotenuzájának nevezzük. A másik két oldalt lábaknak nevezzük. A másik két szögnek nincs külön neve, de mindig komplementer szögek. Érted, hogy miért? A háromszög teljes szögösszege 180 fok, és a derékszög 90 fok, tehát a másik kettőnek is 90 foknak kell lennie.
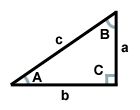
A fenti háromszögnek a c oldal a hipotenúzája, az a és b oldalak a lábai, a C szög pedig a derékszöge. Az A és B szögek komplementer szögek.
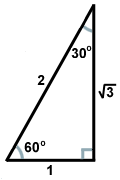
A derékszögű háromszögeknek két típusa van, amelyeket minden matematikusnak jól kell ismernie. Az egyik az a derékszögű háromszög, amely akkor keletkezik, ha egy egyenlő oldalú háromszög egyik csúcsából egy magasságot húzunk, és így két kongruens derékszögű háromszöget alkotunk. A háromszög szögei 30, 60 és 90 fokosak lesznek, ezért kapta a háromszög a nevét: 30-60-90 háromszög. Az oldalhosszúságok aránya az ilyen háromszögekben mindig ugyanaz: ha a 30 fokos szöggel szemben lévő láb hossza x, a 60 fokos szöggel szemben lévő láb hossza x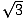
lesz, a derékszöggel szemben lévő hipoténusz pedig 2x. Az alábbiakban egy 30-60-90 háromszöget ábrázolunk.
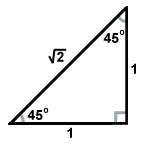
A másik gyakori derékszögű háromszög akkor keletkezik, ha egy átló egy négyzetet két háromszögre oszt. Mindegyik háromszög kongruens, és 45, 45 és 90 fokos szögekkel rendelkezik. Ha a 45 fokos szögekkel szemben lévő lábak hossza x, akkor a hipotenúzának hossza x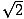
. Ez az arány minden 45-45-90-es háromszögre igaz. A 45-45-90-es háromszögeket gyakran nevezik egyenlő szárú derékszögű háromszögeknek is.
Egy utolsó megjegyzendő tulajdonság, hogy a derékszögű háromszög lábai egyben a háromszög magasságai is. Ezért egy derékszögű háromszög területe a lábak hosszának a fele.