Analisi di regressione logistica

Il risultato nell’analisi di regressione logistica è spesso codificato come 0 o 1, dove 1 indica che il risultato di interesse è presente, e 0 indica che il risultato di interesse è assente. Se definiamo p come la probabilità che il risultato sia 1, il modello di regressione logistica multipla può essere scritto come segue:

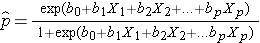
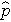è la probabilità attesa che il risultato sia presente; X1 attraverso Xp sono variabili indipendenti distinte; e b0 attraverso bp sono i coefficienti di regressione. Il modello di regressione logistica multipla è talvolta scritto in modo diverso. Nella forma seguente, il risultato è il logaritmo atteso delle probabilità che il risultato sia presente,

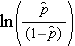
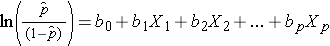
Si noti che il lato destro dell’equazione di cui sopra sembra l’equazione di regressione lineare multipla. Tuttavia, la tecnica per stimare i coefficienti di regressione in un modello di regressione logistica è diversa da quella usata per stimare i coefficienti di regressione in un modello di regressione lineare multipla. Nella regressione logistica i coefficienti derivati dal modello (ad esempio, b1) indicano il cambiamento nelle probabilità logiche attese relative a un cambiamento di un’unità in X1, mantenendo costanti tutti gli altri predittori. Pertanto, l’antilog di un coefficiente di regressione stimato, exp(bi), produce un odds ratio, come illustrato nell’esempio seguente.

Esempio di regressione logistica – Associazione tra obesità e CVD

Abbiamo precedentemente analizzato i dati di uno studio progettato per valutare l’associazione tra obesità (definita come BMI > 30) e malattia cardiovascolare incidente. I dati sono stati raccolti da partecipanti che erano tra i 35 e i 65 anni e senza malattie cardiovascolari (CVD) al basale. Ogni partecipante è stato seguito per 10 anni per lo sviluppo della malattia cardiovascolare. Un riassunto dei dati può essere trovato a pagina 2 di questo modulo. Il rischio relativo non aggiustato o grezzo era RR = 1.78, e l’odds ratio non aggiustato o grezzo era OR =1.93. Abbiamo anche determinato che l’età era un confonditore, e usando il metodo Cochran-Mantel-Haenszel, abbiamo stimato un rischio relativo aggiustato di RRCMH =1,44 e un odds ratio aggiustato di ORCMH =1,52. Useremo ora l’analisi di regressione logistica per valutare l’associazione tra obesità e malattia cardiovascolare incidente aggiustando per l’età.

L’analisi di regressione logistica rivela quanto segue:

Variabile indipendente	Cefficiente di regressione	Chi-quadrato	Valore P
Intercetta	-2.367	307.38	0.0001
Obesità	0,658	9,87	0.0017

Il modello di regressione logistica semplice mette in relazione l’obesità con le probabilità logiche di CVD incidente:

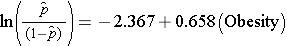
L’obesità è una variabile indicatore nel modello, codificata come segue: 1=obeso e 0=non obeso. Il log odds di CVD incidente è 0,658 volte più alto nelle persone che sono obese rispetto a non obese. Se prendiamo l’antilog del coefficiente di regressione, exp(0,658) = 1,93, otteniamo l’odds ratio grezzo o non aggiustato. Le probabilità di sviluppare CVD sono 1,93 volte più alte tra le persone obese rispetto alle persone non obese. L’associazione tra obesità e CVD incidente è statisticamente significativa (p=0,0017). Si noti che le statistiche di test per valutare la significatività dei parametri di regressione nell’analisi di regressione logistica sono basate su statistiche chi-quadro, al contrario delle statistiche t come nel caso dell’analisi di regressione lineare. Questo perché viene utilizzata una tecnica di stima diversa, chiamata stima di massima verosimiglianza, per stimare i parametri di regressione (vedi Hosmer e Lemeshow3 per i dettagli tecnici).

Molti pacchetti di calcolo statistico generano anche gli odds ratio e gli intervalli di confidenza al 95% per gli odds ratio come parte della loro procedura di analisi di regressione logistica. In questo esempio, la stima dell’odds ratio è 1,93 e l’intervallo di confidenza al 95% è (1,281, 2,913).

Esaminando l’associazione tra obesità e CVD, abbiamo precedentemente determinato che l’età era un confonditore. Nel modello consideriamo ancora due gruppi di età (meno di 50 anni e 50 anni e più). Per l’analisi, il gruppo di età è codificato come segue: 1=50 anni e più e 0=meno di 50 anni.

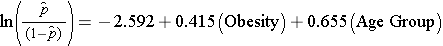
Se prendiamo l’antilog del coefficiente di regressione associato all’obesità, exp(0,415) = 1,52 otteniamo l’odds ratio aggiustato per età. Le probabilità di sviluppare CVD sono 1,52 volte più alte tra le persone obese rispetto alle persone non obese, aggiustando per l’età. Nella sezione 9.2 abbiamo usato il metodo Cochran-Mantel-Haenszel per generare un odds ratio aggiustato per l’età e abbiamo trovato quanto segue:

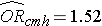
Questo illustra come l’analisi di regressione logistica multipla può essere usata per tenere conto dei fattori di confusione. I modelli possono essere estesi per tenere conto di diverse variabili di confondimento simultaneamente. L’analisi di regressione logistica multipla può anche essere usata per valutare il confondimento e la modifica degli effetti, e gli approcci sono identici a quelli usati nell’analisi di regressione lineare multipla. L’analisi di regressione logistica multipla può anche essere usata per esaminare l’impatto di più fattori di rischio (invece di concentrarsi su un singolo fattore di rischio) su un risultato dicotomico.

Esempio – Fattori di rischio associati al basso peso alla nascita del bambino

Supponiamo che gli investigatori siano anche interessati agli esiti avversi della gravidanza, compreso il diabete gestazionale, la pre-eclampsia (cioè l’ipertensione indotta dalla gravidanza) e il travaglio pre-termine. Ricordiamo che lo studio ha coinvolto 832 donne incinte che hanno fornito dati demografici e clinici. Nel campione dello studio, 22 (2,7%) donne sviluppano la pre-eclampsia, 35 (4,2%) sviluppano il diabete gestazionale e 40 (4,8%) il travaglio pre-termine. Supponiamo di voler valutare se ci sono differenze in ciascuno di questi esiti avversi della gravidanza per razza/etnia, aggiustati per l’età materna. Sono state condotte tre analisi separate di regressione logistica che mettono in relazione ogni risultato, considerato separatamente, con le 3 variabili dummy o indicatori che riflettono la razza della madre e l’età della madre, in anni. I risultati sono riportati di seguito.

Outcome: Pre-eclampsia	Coefficiente di regressione	Chi-quadro	Valore P	Odds Ratio (95% CI)
Intercetta	-3.066	4.518	0.0335	–
Ragazza nera	2.191	12.640	0.0004	8.948 (2.673, 29.949)
Ragazza ispanica	-0.1053	0.0325	0.8570	0.900 (0,286, 2,829)
Altra razza	0,0586	0,0021	0.9046	1,060 (0,104, 3,698)
Età della madre (anni)	-0,0252	0.3574	0.5500	0.975 (0.898, 1.059)

L’unica differenza statisticamente significativa nella pre-eclampsia è tra madri nere e bianche.

Le madri nere hanno quasi 9 volte più probabilità di sviluppare pre-eclampsia delle madri bianche, aggiustate per l’età materna. L’intervallo di confidenza al 95% per l’odds ratio che confronta le donne nere con quelle bianche che sviluppano la pre-eclampsia è molto ampio (da 2,673 a 29,949). Questo è dovuto al fatto che c’è un piccolo numero di eventi di esito (solo 22 donne sviluppano la pre-eclampsia nel campione totale) e un piccolo numero di donne di razza nera nello studio. Quindi, questa associazione dovrebbe essere interpretata con cautela.

Mentre l’odds ratio è statisticamente significativo, l’intervallo di confidenza suggerisce che la grandezza dell’effetto potrebbe essere ovunque da un aumento di 2,6 volte a un aumento di 29,9 volte. Uno studio più grande è necessario per generare una stima più precisa dell’effetto.

Diabete gestazionale	Coefficiente di regressione	Chi-square	Valore P	Odds Ratio (95% CI)
Intercept	-5.823	22,968	0,0001	–
Ragazza nera	1,621	6.660	0,0099	5,056 (1,477, 17,312)
Ragazza ispanica	0,581	1.766	0.1839	1.787 (0.759, 4.207)
Altra razza	1.348	5.917	0.0150	3.848 (1.299, 11.395)
Età della madre (anni)	0.071	4.314	0.0378	1.073 (1.004, 1.147)

Per quanto riguarda il diabete gestazionale, ci sono differenze statisticamente significative tra madri bianche e nere (p=0.0099) e tra madri che si identificano come di altra razza rispetto alle bianche (p=0.0150), aggiustate per l’età della madre. Anche l’età della madre è statisticamente significativa (p=0,0378), con le donne più anziane che hanno più probabilità di sviluppare il diabete gestazionale, aggiustato per razza/etnia.

Outcome: Preterm Labor	Coefficiente di regressione	Chi-quadrato	Valore P	Odds Ratio (95% CI)
Intercept	-1.443	1.602	0.2056	–
Ragazza nera	-0.082	0.015	0.9039	0,921 (0,244, 3,483)
Ragazza ispanica	-1,564	9.497	0,0021	0,209 (0,077, 0,566)
Altra razza	0.548	1.124	0.2890	1.730 (0.628,4.767)
Età della madre (anni.)	00.037	1.198	0.2737	0.963 (0.901, 1.030)

Per quanto riguarda il travaglio pre-termine, l’unica differenza statisticamente significativa è tra madri ispaniche e bianche (p=0.0021). Le madri ispaniche hanno l’80% di probabilità in meno di sviluppare un travaglio pre-termine rispetto alle madri bianche (odds ratio = 0,209), aggiustato per l’età della madre.

I metodi multivariabili sono computazionalmente complessi e generalmente richiedono l’uso di un pacchetto di calcolo statistico. I metodi multivariabili possono essere utilizzati per valutare e regolare il confondimento, per determinare se c’è una modifica dell’effetto, o per valutare le relazioni di diversi fattori di esposizione o di rischio su un risultato simultaneamente. Le analisi multivariabili sono complesse e dovrebbero sempre essere pianificate per riflettere relazioni biologicamente plausibili. Mentre è relativamente facile considerare una variabile aggiuntiva in un modello di regressione lineare multipla o logistica multipla, solo le variabili che sono clinicamente significative dovrebbero essere incluse.

È importante ricordare che i modelli multivariabili possono solo aggiustare o tenere conto delle differenze nelle variabili di confondimento che sono state misurate nello studio. Inoltre, i modelli multivariabili dovrebbero essere usati solo per tenere conto del confondimento quando c’è una certa sovrapposizione nella distribuzione del confondente di ciascun gruppo di fattori di rischio.

Le analisi stratificate sono molto informative, ma se i campioni in strati specifici sono troppo piccoli, le analisi possono mancare di precisione. Nella pianificazione degli studi, i ricercatori devono prestare attenzione ai potenziali modificatori di effetto. Se c’è il sospetto che un’associazione tra un’esposizione o un fattore di rischio sia diversa in gruppi specifici, allora lo studio deve essere progettato per garantire un numero sufficiente di partecipanti in ciascuno di questi gruppi. Le formule di dimensione del campione devono essere utilizzate per determinare il numero di soggetti necessari in ogni strato per garantire un’adeguata precisione o potenza nell’analisi.

torna all’inizio | pagina precedente | pagina successiva