Descrizione semplice
Consideriamo prima il legame pi greco nell’etene da un punto di vista di teoria MO semplificata (in questo esempio trascureremo i legami sigma nella molecola, e penseremo solo al legame π). Iniziamo con due orbitali atomici: un orbitale 2p non ibrido per ogni carbonio. Ognuno contiene un singolo elettrone. Nella teoria MO, i due atomici si combinano matematicamente per formare due orbitali pi molecolari, uno a bassa energia pi di legame e uno ad alta energia pi* anti legame.

Orbitali molecolari per l’etene (etilene)
Nell’orbitale pi di legame, i due lobi ombreggiati degli orbitali p interagiscono costruttivamente tra loro, così come i due lobi non ombreggiati (ricordate, la scelta arbitraria dell’ombreggiatura rappresenta i segni matematici (+) e (-) della funzione d’onda matematica che descrive l’orbitale). C’è una maggiore densità di elettroni tra i due nuclei di carbonio nell’orbitale molecolare – è un’interazione di legame.
Nell’orbitale pi* anti-bonding a più alta energia, il lobo ombreggiato di un orbitale p interagisce distruttivamente con il lobo non ombreggiato del secondo orbitale p, portando a un nodo tra i due nuclei e alla repulsione generale tra i nuclei di carbonio.
Anche in questo caso, usando il principio dell'”accumulo”, mettiamo i due elettroni nell’orbitale molecolare pi di bassa energia e di legame. L’orbitale pi* anti-bonding rimane vuoto.
Descrizione MO più dettagliata dell’etene
La teoria degli orbitali molecolari è stata applicata con molto successo a grandi sistemi coniugati, specialmente quelli contenenti catene di atomi di carbonio con legami singoli e doppi alternati. Un’approssimazione introdotta da Hückel nel 1931 considera solo gli elettroni p delocalizzati che si muovono in un quadro di legami \pi. Questa è, infatti, una versione più sofisticata di un modello a elettroni liberi. Per un corso introduttivo di chimica organica non abbiamo bisogno di usare tutta la matematica di Hückel, ma per coloro che amano sondare più a fondo, un’analisi più dettagliata è data qui.
Il più semplice idrocarburo da considerare che mostra un legame \pi è l’etene (etilene), che è composto da quattro atomi di idrogeno e due di carbonio. Sperimentalmente, sappiamo che gli angoli H-C-H e H-C-C nell’etene sono circa 120°. Questo angolo suggerisce che gli atomi di carbonio sono ibridati sp2, il che significa che un orbitale sp2 singolarmente occupato su un carbonio si sovrappone a un orbitale s singolarmente occupato su ogni H e a un lobo sp2 singolarmente occupato sull’altro C. Così ogni carbonio forma un insieme di tre legami σ: due C-H (sp2 + s) e un C-C (sp2 + sp2) (parte (a) della Figura 13.1. sotto).

Figura 13.1. (a) La struttura σ-bonded è formata dalla sovrapposizione di due serie di orbitali ibridi sp2 del carbonio singolarmente occupati e quattro orbitali 1s dell’idrogeno singolarmente occupati per formare legami di coppia di elettroni. Questo usa 10 dei 12 elettroni di valenza per formare un totale di cinque legami σ (quattro legami C-H e un legame C-C). (b) Un orbitale 2pz non ibridato singolarmente occupato rimane su ogni atomo di carbonio per formare un legame π carbonio-carbonio. (Nota: per convenzione, nelle molecole planari l’asse perpendicolare al piano molecolare è l’asse z.)
L’approssimazione di Hückel è usata per determinare le energie e le forme degli orbitali molecolari \pi nei sistemi coniugati. Nell’approssimazione di Hückel, il legame covalente in questi idrocarburi può essere separato in due “quadri” indipendenti: il quadro di legame \sigma e il quadro di legame \sigma. Le funzioni d’onda usate per descrivere gli orbitali di legame in ogni quadro risultano da diverse combinazioni di orbitali atomici. Il metodo si limita ad affrontare gli idrocarburi coniugati e specificamente si includono solo gli orbitali molecolari di elettroni \più perché questi determinano le proprietà generali di queste molecole; gli elettroni sigma sono ignorati. Questo viene chiamato separabilità sigma-pi ed è giustificato dall’ortogonalità degli orbitali sigma e \pi nelle molecole planari. Per questo motivo, il metodo di Hückel è limitato ai sistemi planari. L’approssimazione di Hückel assume che gli elettroni nei legami \pi “sentano” un potenziale elettrostatico dovuto all’intero quadro di legame \sigma nella molecola (cioè si concentra solo sulla formazione dei legami \pi, dato che il quadro di legame \sigma è già stato formato).
Sistemi coniugati
Un sistema coniugato ha una regione di p-orbitali sovrapposti, a ponte con i legami singoli adiacenti, che permettono una delocalizzazione degli elettroni \pi attraverso tutti i p-orbitali allineati adiacenti. Questi elettroni \pi non appartengono ad un singolo legame o atomo, ma piuttosto ad un gruppo di atomi.
Etene
Prima di considerare il trattamento di Hückel per l’etene, è utile rivedere il quadro generale di legame della molecola. Il legame nell’etene comporta l’ibridazione sp^2 degli orbitali atomici 2s , 2p_x e 2p_y su ogni atomo di carbonio; lasciando gli orbitali 2p_z intatti (Figura 13.2).
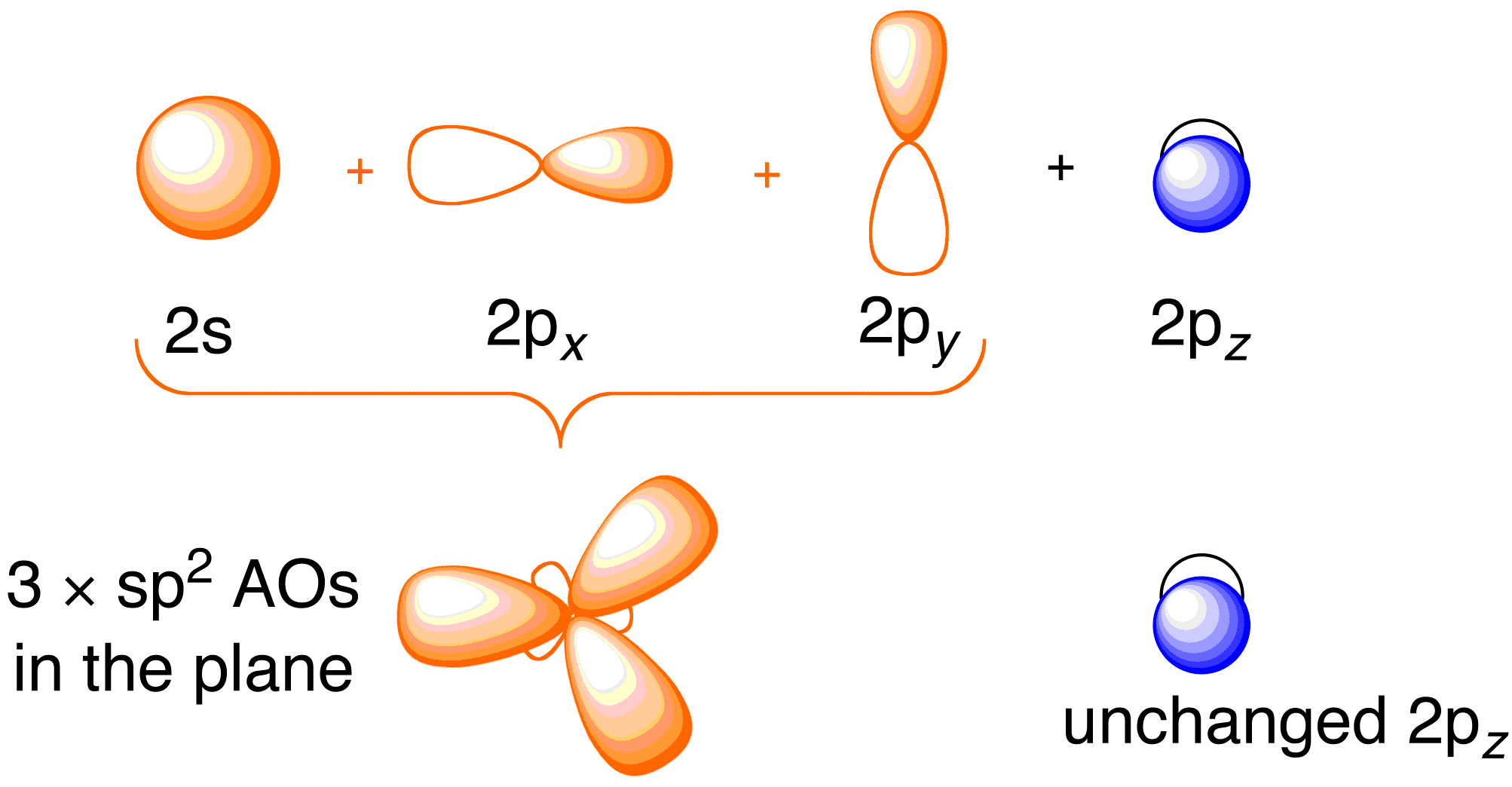
Figura 13.2. Ibridazione degli orbitali atomici del carbonio per dare orbitali ibridi sp^2 per il legame con gli atomi di idrogeno nell’etene. Immagine usata con il permesso di ChemTube (CC-SA-BY-NC; Nick Greeves).
L’uso di orbitali ibridi nell’approccio degli orbitali molecolari qui descritto è solo una comodità e non invoca la teoria del legame di valenza (direttamente). Una descrizione identica può essere estratta usando esclusivamente orbitali atomici sul carbonio, ma l’interpretazione delle funzioni d’onda risultanti è meno intuitiva. Per esempio, l’orbitale molecolare i-esimo può essere descritto tramite orbitali ibridi
o tramite orbitali atomici
dove \a_i\} e \c_i\} sono coefficienti dell’espansione. Entrambe le descrizioni funzionano ed entrambi gli approcci sono identici poiché
dove \c_i\} sono coefficienti che descrivono l’orbitale ibridato.
Il legame avviene tramite la mescolanza degli elettroni negli orbitali ibridi sp^2 sul carbonio e gli elettroni negli orbitali atomici 1s dei quattro atomi di idrogeno (Figura 13.2. in alto a sinistra) dando luogo alla struttura di legame \sigma. Il quadro di legame \pi risulta dagli orbitali 2p_z non ibridizzati (Figura 13.2. sopra, a destra). L’indipendenza di queste due strutture è dimostrata nel diagramma degli orbitali molecolari risultante nella figura qui sotto; la teoria di Hückel si occupa solo di descrivere gli orbitali molecolari e le energie della struttura di legame \pi.

Figura 13.3: Orbitali molecolari che dimostrano la separabilità sigma-pi della struttura di legame \pi (blu) e delle strutture di legame \sigma (rosso) dell’etilene.
Il trattamento di Hückel si occupa solo di descrivere gli orbitali molecolari e le energie della struttura di legame \pi.
Siccome la teoria di Hückel è una considerazione speciale della teoria degli orbitali molecolari, gli orbitali molecolari \psi_i possono essere descritti come una combinazione lineare degli orbitali atomici 2p_z \phi al carbonio con i loro corrispondenti coefficienti \c_i\}:
Per l’analisi completa della chimica quantistica usando l’equazione di Schrödinger (non richiesta per il corso di chimica organica), vedi questa pagina Libretexts.
Questi orbitali molecolari formano la struttura di legame π e poiché ogni carbonio contribuisce un elettrone a questa struttura, solo l’orbitale molecolare più basso ( | \psi_1 \rangle ) è occupato (Figura ) nello stato fondamentale. La configurazione elettronica corrispondente è quindi \pi_1^2 .

Figura 13.4: Rappresentazione schematica del quadro degli orbitali molecolari \pi per l’etilene. Si noti che l’orbitale molecolare antibonding ha un nodo in più rispetto all’orbitale molecolare bonding, come ci si aspettava, poiché è più alto in energia.
HOMO e LUMO sono acronimi per orbitale molecolare più alto occupato e orbitale molecolare più basso non occupato, rispettivamente, e sono spesso indicati come orbitali di frontiera. La differenza di energia tra l’HOMO e il LUMO è chiamata gap HOMO-LUMO.
Gli orbitali molecolari calcolati 3-D \pi sono mostrati nella figura 13.5.

Figura 13.5: Orbitali molecolari \pi calcolati per l’etilene. (a sinistra) l’orbitale di legame (ψ1) e (a destra) l’orbitale di anti-bonding (ψ2).
Contribuenti
- Seymour Blinder (professore emerito di chimica e fisica all’Università del Michigan, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
