In una distribuzione normale, i dati sono distribuiti simmetricamente senza asimmetrie. Se tracciati su un grafico, i dati seguono una forma a campana, con la maggior parte dei valori che si raggruppano intorno a una regione centrale e si assottigliano man mano che si allontanano dal centro.
Le distribuzioni normali sono anche chiamate distribuzioni gaussiane o curve a campana a causa della loro forma.

- Perché le distribuzioni normali sono importanti?
- Quali sono le proprietà delle distribuzioni normali?
- Qual è il tuo punteggio di plagio?
- Regola empirica
- Teorema del limite centrale
- Formula della curva normale
- Qual è la distribuzione normale standard?
- Trovare la probabilità usando la distribuzione z
- Domande frequenti sulle distribuzioni normali
Perché le distribuzioni normali sono importanti?
Tutti i tipi di variabili nelle scienze naturali e sociali sono distribuite normalmente o approssimativamente normalmente. Altezza, peso alla nascita, capacità di lettura, soddisfazione sul lavoro o punteggi SAT sono solo alcuni esempi di tali variabili.
Perché le variabili distribuite normalmente sono così comuni, molti test statistici sono progettati per popolazioni distribuite normalmente.
Comprendere le proprietà delle distribuzioni normali significa che puoi usare la statistica inferenziale per confrontare gruppi diversi e fare stime sulle popolazioni usando campioni.
Quali sono le proprietà delle distribuzioni normali?
Le distribuzioni normali hanno caratteristiche chiave che sono facili da individuare nei grafici:
- Media, mediana e modalità sono esattamente le stesse.
- La distribuzione è simmetrica intorno alla media – metà dei valori cade sotto la media e metà sopra la media.
- La distribuzione può essere descritta da due valori: la media e la deviazione standard.


La media è il parametro di localizzazione mentre la deviazione standard è il parametro di scala.
La media determina dove il picco della curva è centrato. Aumentando la media si sposta la curva a destra, mentre diminuendola si sposta la curva a sinistra.


La deviazione standard allunga o comprime la curva. Una piccola deviazione standard risulta in una curva stretta, mentre una grande deviazione standard porta ad una curva larga.


Regola empirica
La regola empirica, o la regola 68-95-99.7, ti dice dove si trova la maggior parte dei tuoi valori in una distribuzione normale:
- Circa il 68% dei valori sono entro 1 deviazione standard dalla media.
- Circa il 95% dei valori sono entro 2 deviazioni standard dalla media.
- Circa il 99,7% dei valori sono entro 3 deviazioni standard dalla media.
Seguendo la regola empirica:
- Circa il 68% dei punteggi sono tra 1000 e 1300, 1 deviazione standard sopra e sotto la media.
- Circa il 95% dei punteggi sono tra 850 e 1450, 2 deviazioni standard sopra e sotto la media.
- Circa il 99,7% dei punteggi sono tra 700 e 1600, 3 deviazioni standard sopra e sotto la media.


La regola empirica è un modo veloce per avere una visione d’insieme dei tuoi dati e controllare eventuali outlier o valori estremi che non seguono questo schema.
Se i dati di piccoli campioni non seguono strettamente questo schema, allora altre distribuzioni come la distribuzione t possono essere più appropriate. Una volta identificata la distribuzione della vostra variabile, potete applicare i test statistici appropriati.
Teorema del limite centrale
Il teorema del limite centrale è la base di come funzionano le distribuzioni normali in statistica.
Nella ricerca, per avere una buona idea della media di una popolazione, idealmente dovreste raccogliere dati da più campioni casuali all’interno della popolazione. Una distribuzione di campionamento della media è la distribuzione delle medie di questi diversi campioni.
Il teorema del limite centrale mostra quanto segue:
- Legge dei grandi numeri: All’aumentare della dimensione del campione (o del numero di campioni), la media del campione si avvicinerà alla media della popolazione.
- Con più grandi campioni, la distribuzione del campione della media è distribuita normalmente, anche se la variabile originale non è distribuita normalmente.
I test statistici parametrici tipicamente assumono che i campioni provengano da popolazioni normalmente distribuite, ma il teorema del limite centrale significa che questa assunzione non è necessaria da soddisfare quando si ha un campione abbastanza grande.
Si possono usare test parametrici per grandi campioni da popolazioni con qualsiasi tipo di distribuzione, purché siano soddisfatte altre importanti ipotesi. Una dimensione del campione di 30 o più è generalmente considerata grande.
Per i piccoli campioni, l’assunzione di normalità è importante perché la distribuzione campionaria della media non è nota. Per ottenere risultati accurati, dovete essere sicuri che la popolazione sia distribuita normalmente prima di poter usare test parametrici con piccoli campioni.
Formula della curva normale
Una volta che avete la media e la deviazione standard di una distribuzione normale, potete adattare una curva normale ai vostri dati usando una funzione di densità di probabilità.


In una funzione di densità di probabilità, l’area sotto la curva indica la probabilità. La distribuzione normale è una distribuzione di probabilità, quindi l’area totale sotto la curva è sempre 1 o 100%.
La formula della funzione di densità di probabilità normale sembra abbastanza complicata. Ma per usarla, hai solo bisogno di conoscere la media e la deviazione standard della popolazione.
Per qualsiasi valore di x, puoi inserire la media e la deviazione standard nella formula per trovare la densità di probabilità della variabile che assume quel valore di x.
| Formula della densità di probabilità normale | Spiegazione |
|---|---|
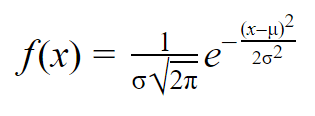 |
|
Sul tuo grafico della funzione di densità di probabilità, la probabilità è l’area ombreggiata sotto la curva che si trova a destra di dove i punteggi SAT sono uguali a 1380.


Puoi trovare il valore di probabilità di questo punteggio usando la distribuzione normale standard.
Qual è la distribuzione normale standard?
La distribuzione normale standard, chiamata anche distribuzione z, è una speciale distribuzione normale dove la media è 0 e la deviazione standard è 1.
Ogni distribuzione normale è una versione della distribuzione normale standard che è stata allungata o schiacciata e spostata orizzontalmente a destra o a sinistra.


Mentre le singole osservazioni delle distribuzioni normali sono indicate come x, esse sono indicate come z nella distribuzione z. Ogni distribuzione normale può essere convertita alla distribuzione normale standard trasformando i singoli valori in punteggi z.
I punteggi z ti dicono quante deviazioni standard dalla media si trova ogni valore.


Ti basta conoscere la media e la deviazione standard della tua distribuzione per trovare lo z-score di un valore.
| Formula del punteggio Z | Spiegazione |
|---|---|
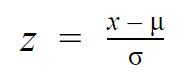 |
|
Convertiamo le distribuzioni normali nella distribuzione normale standard per diverse ragioni:
- Per trovare la probabilità che le osservazioni in una distribuzione cadano sopra o sotto un dato valore.
- Per trovare la probabilità che la media di un campione differisca significativamente dalla media di una popolazione nota.
- Per confrontare i punteggi di diverse distribuzioni con diverse medie e deviazioni standard.
Trovare la probabilità usando la distribuzione z
Ogni valore z è associato a una probabilità, o valore p, che vi dice la probabilità che si verifichino valori inferiori a quel valore z. Se si converte un valore individuale in uno z-score, si può poi trovare la probabilità che tutti i valori fino a quel valore si verifichino in una distribuzione normale.
La media della nostra distribuzione è 1150, e la deviazione standard è 150. Lo z-score ti dice quante deviazioni standard sono lontane da 1380 dalla media.
| Formula | Calcolo |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
Per un punteggio z di 1,53, il valore p è 0,937. Questa è la probabilità che i punteggi SAT siano 1380 o meno (93,7%), ed è l’area sotto la curva a sinistra dell’area ombreggiata.


Per trovare l’area ombreggiata, bisogna togliere 0.937 da 1, che è l’area totale sotto la curva.
Probabilità di x>1380 = 1 – 0,937 = 0,063
Questo significa che è probabile che solo il 6,3% dei punteggi SAT nel tuo campione superi 1380.
Domande frequenti sulle distribuzioni normali
In una distribuzione normale, i dati sono distribuiti simmetricamente senza asimmetria. La maggior parte dei valori si raggruppa intorno a una regione centrale, con valori che si assottigliano man mano che si allontanano dal centro.
Le misure di tendenza centrale (media, modo e mediana) sono esattamente le stesse in una distribuzione normale.
La distribuzione normale standard, chiamata anche distribuzione z, è una speciale distribuzione normale dove la media è 0 e la deviazione standard è 1.
Qualsiasi distribuzione normale può essere convertita nella distribuzione normale standard trasformando i singoli valori in punteggi z. In una distribuzione z, i punteggi z ti dicono quante deviazioni standard dalla media si trova ogni valore.
La regola empirica, o la regola 68-95-99.7, ti dice dove si trova la maggior parte dei valori in una distribuzione normale:
- Circa il 68% dei valori sono entro 1 deviazione standard dalla media.
- Circa il 95% dei valori sono entro 2 deviazioni standard dalla media.
- Circa il 99,7% dei valori sono entro 3 deviazioni standard della media.
La regola empirica è un modo veloce per avere una visione d’insieme dei tuoi dati e controllare eventuali outlier o valori estremi che non seguono questo schema.
La distribuzione t è un modo di descrivere un insieme di osservazioni in cui la maggior parte delle osservazioni cadono vicino alla media, e il resto delle osservazioni costituiscono le code su entrambi i lati. È un tipo di distribuzione normale usata per campioni più piccoli, dove la varianza dei dati è sconosciuta.
La distribuzione t forma una curva a campana quando è tracciata su un grafico. Può essere descritta matematicamente usando la media e la deviazione standard.

