ロジスティック回帰分析の結果は、しばしば0か1でコード化され、1は関心のある結果があることを示し、0は関心のある結果がないことを示す。 p を結果が1である確率と定義すると，多重ロジスティック回帰モデルは，次のように書ける：
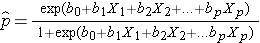
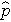は結果が存在する期待確率，X1 から Xp は個別の独立変数，b0 から bp は回帰係数である． 多重ロジスティック回帰モデルは，時々，別の書き方をする． 次の形式では，結果は，結果が存在するオッズの期待対数である,
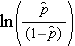
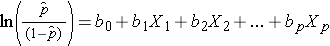
上の式の右辺が重回帰式のように見えることに注意すること． しかし、ロジスティック回帰モデルで回帰係数を推定する手法は、重回帰モデルで回帰係数を推定する手法とは異なる。 ロジスティック回帰では，モデルから得られる係数（たとえば，b1）は，他のすべての予測変数を一定にして，X1 の1ユニット変化に対する期待対数オッズの変化を示す． したがって、推定回帰係数のアンチログ、exp(bi)は、以下の例に示すように、オッズ比を生成する。
ロジスティック回帰の例-肥満とCVDとの関連
我々は以前に、肥満（BMI > 30と定義）と心血管疾患発症との関連を評価するために設計された研究からデータを分析した。 35歳から65歳で、ベースライン時に心血管疾患（CVD）のない参加者からデータが収集された。 各受験者は、心血管疾患の発症について10年間追跡調査されました。 データの要約はこのモジュールの2ページ目にあります。 未調整または粗い相対リスクはRR = 1.78で、未調整または粗いオッズ比はOR = 1.93であった。 また、年齢が交絡因子であると判断し、Cochran-Mantel-Haenszel法を用いて、修正相対リスクはRRCMH=1.44、修正オッズ比はORCMH=1.52と推定されました。 次に、ロジスティック回帰分析を用いて、年齢を調整した肥満と心血管疾患の発症との関連を評価する。
ロジスティック回帰分析により、以下のことが明らかになった。
|
独立変数 |
回帰係数 |
カイ二乗 |
P値 |
|---|---|---|---|
|
Intercept |
-2.2.367 |
307.38 |
0.0001 |
|
Obesity |
0.658 |
0.0.0017 |
単純ロジスティック回帰モデルは、肥満をCVD発症の対数オッズに関連付ける：
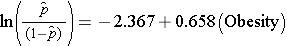
肥満はモデル中の指標変数で、次のようにコード化される。 1=肥満、0=肥満でない。 肥満の人のCVD発症の対数オッズは、肥満でない人に比べて0.658倍高い。 回帰係数の反比例をとると、exp(0.658) = 1.93で、粗オッズ比または未調整オッズ比が得られる。 肥満の人がCVDを発症するオッズは、非肥満の人に比べて1.93倍も高いことがわかる。 肥満とCVD発症の関連は、統計的に有意である（p=0.0017）。 ロジスティック回帰分析の回帰パラメータの有意性を評価する検定統計は、線形回帰分析の場合のt統計とは対照的に、カイ二乗統計に基づいていることに注意してください。
多くの統計計算パッケージは、ロジスティック回帰分析の手順の一部として、オッズ比とオッズ比の95％信頼区間をも生成しています。 この例では、オッズ比の推定値は1.93、95％信頼区間は（1.281、2.913）である。
肥満とCVDとの関連を調べる際に、年齢が交絡因子であると以前に判断した。以下の多重ロジスティック回帰モデルは、年齢を調整して肥満とCVD発症との関連を推定している。 このモデルでは、再び2つの年齢群（50歳未満と50歳以上）を考慮する。 分析のために、年齢群は以下のようにコード化されている。 1=50歳以上、0=50歳未満とした。
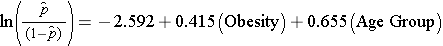
肥満に関連する回帰係数の反比例をとると、exp(0.415) = 1.52 年齢調整後のオッズ比が求められる。 年齢を調整すると肥満者では非肥満者に比べてCVD発症のオッズが1.52倍高くなることがわかる。 9.2節でコクラン・マンテル・ヘーンスゼル法を用いて年齢調整したオッズ比を出したところ、以下のようになりました：
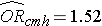
これは交絡を説明するために多重ロジスティック回帰分析がどのように使われるかを説明しています。 モデルは、いくつかの交絡変数を同時に考慮するように拡張することができます。 多重ロジスティック回帰分析は、交絡と効果修飾を評価するために使用することもでき、そのアプローチは多重線形回帰分析で使用するものと同じである。
例-低出生体重児に関連する危険因子
研究者が妊娠糖尿病、子癇前症（すなわち、妊娠による高血圧）、早産などの有害妊娠結果にも関心を持っているとする。 この研究には、人口統計学的および臨床的データを提供する832人の妊婦が参加していることを思い出してほしい。 この研究では、22人（2.7％）が子癇前症、35人（4.2％）が妊娠糖尿病、40人（4.8％）が早産を発症していることがわかりました。 これらの有害な妊娠転帰のそれぞれに、母体年齢で調整した人種／民族による違いがあるかどうかを評価したいとする。 各結果を別々に考え、母親の人種と母親の年齢（年）を反映した3つのダミーまたは指標変数と関連付ける3つの別々のロジスティック回帰分析を行った。 その結果は以下の通りである。
|
Outcome: 子癇前症 |
回帰係数 |
カイ二乗 |
P値 |
オッズ比（95%CI） |
|---|---|---|---|---|
|
切片 |
-3.066 |
4.518 |
0.0335 |
– |
|
黒人 |
||||
|
Hispanic race |
-0.1053 |
0.901> |
||
|
その他の人種 |
0.0586 |
1.060 (0.104, 3.698) |
||
|
母親の年齢（歳） |
-0.0252 |
1.060 (1.060, 1.040) 0.3574 |
0.5500 |
0.975 (0.898, 1.059) |
子癇前症の統計的有意差は黒人母親と白人母親のみ。
黒人の母親の子癇前症を起こす確率は白人母親より母親の年齢で調整すると約9倍である。 子癇前症を発症した黒人女性と白人女性を比較したオッズ比の95％信頼区間は非常に広い（2.673～29.949）。 これは、アウトカムイベントの数が少ないこと（全標本中、子癇前症を発症した女性は22人しかいない）、および研究中の黒人の女性の数が少ないことに起因している。 したがって、この関連は慎重に解釈されるべきである。
オッズ比は統計的に有意であるが、信頼区間から、効果の大きさは2.6倍増から29.9倍増までのいずれかになる可能性があることが示唆された。 より正確な効果の推定を行うには、より大規模な研究が必要である。
|
妊娠糖尿病 |
回帰係数 |
チー二乗 |
P値 |
オッズ比（95％CI） |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
切片 |
-5.823 |
22.968 |
– |
|||||||||
|
– – |
– | – | – | – | – | — | – | — | – | – | — |
0.0099 |
|
Hispanic race |
1.460 |
1.460 |
0.581 |
2.460 1.460 |
0.460 |
0.460 | 0.440766 |
0.1839 |
||||
|
Other race |
3.0 |
1.0 1.0 |
2.0 |
2.0 |
0.0 |
2.0 |
2.0 |
2.0917 |
0.0150 |
|||
|
母親の年齢（歳） |
0.071 |
4.999 (1.299, 11.395).399 (0.999).314 |
0.0378 |
1.073 (1.004, 1.147) |
妊娠糖尿病に関連して、母親年齢で調整すると黒人と白人母親（p=0.0099）と自分を白人と他の人種としている母親（p=0.0150）で統計的に有意差があることがわかる。 母親の年齢も統計的に有意であり（p=0.0378）、高齢の女性ほど妊娠糖尿病を発症しやすく、人種・民族で調整されています。
|
Outcome: 早産 |
回帰係数 |
カイ二乗 |
P値 |
オッズ比（95%CI） |
|---|---|---|---|---|
|
Intercept |
-1.443 |
1.602 |
0.2056 |
– |
|
Black race |
-0.082 |
0.9039 |
0.921 (0.244, 3.483) |
|
|
Hispanic race |
-1.564 |
0.0021 |
0.209 (0.077, 0.566) |
|
|
Other race |
0.0021 |
0.0021(0.0021)です。548 |
1.124 |
0.2890 |
|
母の年齢 (years.)) |
00.037 |
1.198 |
0.2737 |
早産に関して唯一統計上有意差はヒスパニックと白人母親の間にある (p=0.0021). ヒスパニック系の母親は、母親の年齢で調整すると、白人の母親よりも早産になる確率が80％低い（オッズ比＝0.209）。
多変量解析法は計算が複雑で、一般に統計計算パッケージの使用が必要である。 多変量解析法は交絡の評価と調整、効果の修正があるかどうかの判断、あるいは結果に対する複数の曝露またはリスク因子の関係を同時に評価するために用いることができる。 多変量解析は複雑であり、生物学的に妥当な関係を反映するように常に計画されるべきである。 多重線形回帰モデルや多重ロジスティック回帰モデルで追加の変数を考慮することは比較的容易であるが、臨床的に意味のある変数のみを含めるべきである。 さらに，多変量モデルは，危険因子群ごとに交絡因子の分布に重複がある場合にのみ交絡を説明するために使用すべきである。
層別分析は非常に有益であるが，特定の層のサンプルが少なすぎると，分析の精度が低くなる可能性がある。 研究の計画にあたっては、研究者は潜在的な効果修飾因子に十分な注意を払う必要がある。 曝露や危険因子の関連性が特定の集団で異なることが疑われる場合、それらの各群で十分な数の参加者を確保するように研究を計画しなければならない。 解析において十分な精度又は検出力を確保するために、各層で必要な被験者数を決定するために、サンプルサイズの公式を使用しなければならない。
トップへ戻る｜前のページ｜次のページへ戻る