正規分布では、データは対称に分布し、傾きはない。 グラフにするとベル型になり、ほとんどの値は中心付近に集まり、中心から離れるにつれて先細りになります。
正規分布は、その形状からガウス分布やベル曲線とも呼ばれます。

Why do normal distributions matter?
自然科学および社会科学のすべての種類の変数は正規分布またはほぼ正規分布しています。 身長、出生時の体重、読書能力、仕事の満足度、SATスコアなどはその一例です。
正規分布の変数は非常に一般的なので、多くの統計テストは正規分布の集団のために設計されています。
正規分布の特性を理解することは、推測統計を使用して異なるグループを比較し、サンプルを使用して集団についての推定を行うことができることを意味します。
正規分布の特性とは何ですか。


mean is the location parameter while the standard deviation is the scale parameter.
the mean determines where the peak of the curve is centraled.
the mean will be a single parameter.The average is the peak of the curve will be central.


The standard deviation stretched or squeeze the curve.平均を大きくすると曲線は右に、小さくすると左に移動します。


Empirical rule
The empirical rule.は、経験則のことです。 または68-95-99と呼ばれています。7の法則は、正規分布の中でほとんどの値がどこにあるかを教えてくれます。
- 約68%の値が平均から1標準偏差以内にある。
- 約95%の値が平均から2標準偏差以内にある。
経験則に従う:
- 68%前後のスコアが1000~1300で、平均より1標準偏差上と下にある。
- スコアの約95%は850から1450の間で、平均の上下に2標準偏差。
- スコアの約99.7%は700から1600の間で、平均の上下に3標準偏差。


経験則はデータの概要を把握し、このパターンに従わない外れ値や極値を確認する手軽な方法です。
小さなサンプルからのデータではこのパターンにほとんど従わない場合、t分布などの他の分布がより適している可能性があります。 変数の分布を特定したら、適切な統計的検定を適用できる。
中心極限定理
研究において、集団平均の良いアイデアを得るには、理想的には集団内の複数のランダムなサンプルからデータを収集することである。 平均の標本分布とは、これらの異なる標本の平均の分布である。
中心極限定理は、次のことを示している。 サンプルサイズ(またはサンプル数)を増やすと、次にサンプル平均は母平均に近づく。
パラメトリック統計検定は通常、サンプルが正規分布の母集団から来ることを仮定しますが、中心極限定理は、十分に大きなサンプルがあればこの仮定を満たす必要がないことを意味します。
他の重要な仮定が満たされる限り、あらゆる種類の分布を持つ集団から大きなサンプルを対象にパラメトリック検定を使用することが可能です。 30以上のサンプルサイズは一般的に大きいと見なされます。
小さなサンプルでは、平均のサンプリング分布がわからないので、正規性の仮定が重要です。 正確な結果を得るためには、母集団が正規分布であることを確認してから、小さなサンプルでパラメトリック検定を使用する必要があります。
正規曲線の公式
正規分布の平均と標準偏差がわかれば、確率密度関数を使ってデータに正規曲線を当てはめることができます。


確率密度関数では、曲線下の領域で確率を知ることができます。 正規分布は確率分布ですから、曲線の下の面積の合計は常に1または100%です。
正規確率密度関数の公式はかなり複雑に見えます。
x の任意の値について、平均と標準偏差を式にプラグインして、その値 x をとる変数の確率密度を求めることができる。
| 正規確率密度式 | 説明 |
|---|---|
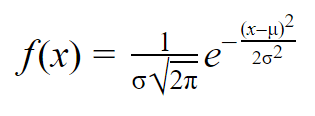 |
|
確率密度関数のグラフで、確率はSATスコアが1380になる場所の右側にある曲線の下の陰の部分である。


このスコアの確率値は標準正規分布を使って求めることができます。
標準正規分布とは何ですか。
標準正規分布はz分布とも呼ばれ、平均が0、標準偏差が1の特殊な正規分布です。
すべての正規分布は、標準正規分布を伸縮させて水平方向に右か左に動かしたバージョンです。


正規分布からの個々の観測値はxと呼ばれるが、それらはz分布のzと呼ばれる。 7927>
Z スコアは、各値が平均から何標準偏差離れているかを示します。


ある値の Z スコアを見つけるには、分布の平均と標準偏差を知るだけでよいのです。
| Zスコアの公式 | 説明 |
|---|---|
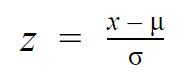 |
|
いくつかの理由で正規分布を標準正規分布に変換しているのである。
- ある分布の観測値が与えられた値より上か下かになる確率を求めるため。
- サンプル平均が既知の母平均と有意に異なる確率を求める。
- 異なる平均と標準偏差を持つ異なる分布のスコアを比較する。
z 分布を使用して確率を求める
各 z スコアは確率、または p 値と関連しており、その z スコア以下の値が発生する可能性を教えてくれる。 個々の値を z スコアに変換すると、その値までのすべての値が正規分布で発生する確率を求めることができます。
この分布の平均は 1150 で、標準偏差は 150 です。 z-スコアは、1380が平均から何標準偏差離れているかを示しています。
| 式 | 計算 |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.標準偏差は、平均と標準偏差の差です。53 |
zスコアが1.53の場合、p値は0.937となる。 これは、SATスコアが1380点以下である確率(93.7%)であり、斜線部の左側の曲線下の面積です。


斜線部を求めるために0をとりますが、これは、0.7927>
Probability of x>1380 = 1 – 0.937 = 0.063
つまり、サンプル中の SAT スコアの 6.3% だけが 1380 を超える可能性があります。
正規分布についてのよくある質問
正規分布では、データは傾きのない対称的な分布をしています。 ほとんどの値は中心付近に集まり、中心から離れるにつれて値は先細りになります。
中心傾向の指標(平均、最頻値、中央値)は、正規分布ではまったく同じになります。
標準正規分布は z 分布とも呼ばれ、平均が 0、標準偏差が 1 の特殊な正規分布です。
任意の正規分布は、個々の値を z スコアにすると、標準正規分布に変換することができます。 z分布では、zスコアは、各値が平均から何標準偏差離れたところにあるかを教えてくれます。
経験則、または 68-95-99.7 規則は、ほとんどの値が正規分布のどこにあるかを教えてくれます:
- 約 68% の値が平均の 1 標準偏差以内にあります。
- 約99.7%の値が平均から3標準偏差以内にある。
経験則は、データの概要を把握し、このパターンに従わない外れ値や極値をチェックする簡単な方法です。
t分布とは、ほとんどの観測値が平均値の近くに位置し、残りの観測値が左右のテールを構成している観測値の集合を記述する方法です。 標本数が少なく、データの分散が不明な場合に用いられる正規分布の一種です。 平均と標準偏差を使って数学的に記述することができる。

