直角が1つある三角形を直角三角形といいます。 直角の反対側の辺は三角形の斜辺と呼ばれます。 他の2つの辺は脚と呼ばれます。 他の2つの角は特別な名前はありませんが、必ず補角になります。 なぜかわかりますか？ 三角形の角の合計は180度で、直角は90度ですから、他の2つの角の合計は90度にならなければなりません。
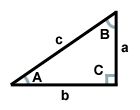
上の三角形は辺cを斜辺、辺aと辺bを脚、角Cを直角としています。 角Aと角Bは補角である。
数学者なら誰でもよく知っている直角三角形には2種類あります。 一つは正三角形の頂点から高度を引いたときにできる直角三角形で、二つの合同な直角三角形ができる。 この三角形の角は30度、60度、90度となり、30-60-90の三角形という名前がついている。 このような三角形の辺の長さの比は常に同じで、30度の角の反対側の足の長さがxなら、60度の角の反対側の足はx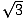
となり、直角を挟んだ斜辺は2xとなる。 下の写真は30-60-90の三角形です。
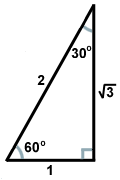
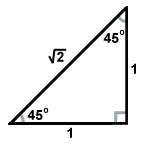
もう一つの一般的な直角三角形は、対角線が正方形を二つの三角形に分割するときにできる一対の三角形からできています。 これらの三角形はそれぞれ合同であり、45度、45度、90度の角度を持つ。 45度の角の反対側の脚の長さをxとすると、斜辺はx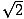
の長さを持つ。 この比率は45-45-90の三角形全てに当てはまる。 45-45-90の三角形はよく二等辺三角形とも呼ばれます。
最後に、直角三角形の脚は三角形の高度でもあることに注意しましょう。 したがって、直角三角形の面積は脚の長さの積の2分の1である。