Hoy, voy a enseñarte una de las habilidades más importantes que puedes poseer cuando se trata de tocar el ukelele (o cualquier tipo de música para el caso): cómo transponer una canción.
Hay muchas razones por las que querrías transponer una canción.
Razón nº 1: Cantabilidad
¿Alguna vez has intentado tocar una canción en el ukelele pero te ha resultado imposible cantarla porque la tonalidad era demasiado alta o demasiado baja? Para solucionar este problema, puedes transponer o cambiar la tonalidad de la canción o la tabla de acordes para que sea más fácil de cantar.
Razón #2: Tocabilidad
Muchas canciones están escritas en tonalidades extrañas como Mib, Fa# o Re. Los acordes que se encuentran en estas tonalidades no son los más fáciles de tocar en el ukelele, así que puedes transponer la canción a una tonalidad diferente con acordes más fáciles.
Razón #3: Creatividad
Transponer te permite ser realmente creativo. Puedes transponer una canción para obtener un tono específico de un conjunto diferente de acordes. También necesitas transponer una canción si intentas arreglar dos canciones diferentes para que fluyan juntas en forma de popurrí (por ejemplo, Somewhere Over the Rainbow -> I’m Yours).
Nunca se sabe cuándo puedes necesitar cambiar la tonalidad de una canción, así que vamos a ver una fórmula fácil de cómo podemos hacerlo.
Cómo transponer una canción
En primer lugar, transponer una canción no es difícil. Sin embargo, tenemos que familiarizarnos con algo de teoría musical básica para poder hacerlo bien. Para esta lección, querrás asegurarte de que estás familiarizado con cómo se forman las escalas mayores.
Para aquellos de ustedes que son perezosos (está bien), he incluido una hoja de trucos en la parte inferior de esta lección. No obstante, os animo a seguir leyendo, porque si conocemos estos conceptos básicos, podemos transponer cualquier canción en nuestra cabeza en cuestión de segundos.
Análisis de números romanos
Cuando transpongo una canción, utilizo una técnica muy común llamada análisis de números romanos. Esto significa que cada acorde de una canción tiene un número romano específico que se le puede asignar.
Hace tiempo, escribí un post llamado Escalas de Ukelele explicadas para principiantes. En ese post, aprendimos que la escala mayor es la escala más popular utilizada en la música hoy en día. Al ver cómo se forma una escala mayor, aprendimos que hay siete notas en la escala.
Para los propósitos de esta lección, necesitas saber que podemos tomar cada una de las siete notas de una escala mayor y construir un acorde a partir de cada nota usando las otras notas de la escala.
No voy a entrar en la teoría de cómo se construyen esos acordes, pero lo más importante es saber que en cualquier clave, hay siete acordes principales. Algunos acordes serán mayores en calidad, y otros serán menores en calidad. En una tonalidad mayor, un acorde será disminuido. (Haga clic aquí para saber más sobre las diferentes calidades de los acordes.)
Para una escala mayor, podemos representar los siete acordes en números romanos:
Una nota importante a añadir es que el hecho de que estemos tratando con claves mayores no significa que todos los acordes dentro de esa clave sean mayores. Una tonalidad mayor tendrá una combinación de acordes mayores, menores y disminuidos.
En la tabla anterior, los acordes mayores se representan en mayúsculas. Los acordes menores se representan en minúsculas. El acorde en minúscula con un círculo en superíndice es un acorde disminuido.
Así que, por ejemplo, tomemos las notas de una escala de Do mayor, en orden ascendente (Do, Re, Mi, Fa, Sol, La, Si), y «enchufémoslas» en los números romanos anteriores. Esto nos dará los acordes utilizados en la tonalidad de Do mayor.
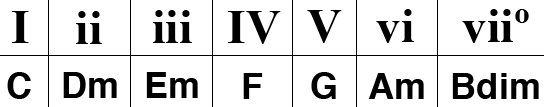
Podemos hacer esto con cualquier tonalidad suponiendo que conocemos las notas que se encuentran en una determinada escala mayor.
Poniéndolo todo junto
Cuando pensamos en los acordes en términos de números romanos, somos capaces de cambiar o transponer fácilmente la tonalidad de una canción.
Por ejemplo, digamos que tenemos una canción en la tonalidad de Do mayor, pero queremos tocarla en la tonalidad de Sol mayor. Utilicemos Somewhere Over the Rainbow como ejemplo.
Los cuatro primeros acordes de la estrofa de Somewhere Over the Rainbow son Do, Em, Fa y Do. Sin embargo, queremos transponer estos acordes a la tonalidad de Sol.
Primero, vamos a representar esos cuatro acordes en la tonalidad de Do mayor como números romanos. Me refiero simplemente a la tabla de arriba.

Esto significa que los cuatro primeros acordes de la estrofa de Somewhere Over the Rainbow son un acorde I, iii, IV y I.
Como queremos transponer a Sol mayor, necesitamos saber cómo se representan los acordes en Sol mayor como números romanos. Si construimos una escala mayor, sabemos que las siete notas de una escala de sol mayor son sol, la, si, do, re, mi y fa#.
Coloquemos esas notas en nuestros números romanos como hicimos para nuestra escala de do mayor.
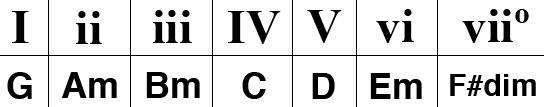
Como podemos ver, los acordes I, iii y IV en la tonalidad de Sol mayor son Sol, Si y Do.

¡Hemos transpuesto con éxito los cuatro primeros acordes de Somewhere Over the Rainbow de Do mayor a Sol mayor! A partir de aquí te dejo transponer el resto de los acordes de la canción.
Hoja de trucos de transposición
Aprender a ver los acordes como números romanos es la mejor manera de poder transponer una canción. Si estás empezando a entender todo esto, puede ser un poco abrumador tratar de averiguar las notas y los acordes de cada escala mayor (¡hay un total de doce!).
Por eso he creado esta hoja de trucos para que puedas consultarla siempre que necesites cambiar la tonalidad de una canción. Enjoy!
Key | I ii iii IV V vi viiº
C major | C Dm Em F G Am Bdim
Db major | Db Ebm Fm Gb Ab Bbm Cdim
D major | D Em F#m G A Bm C#dim
Eb major | Eb Fm Gm Ab Bb Cm Ddim
E major | E F#m G#m A B C#m D#dim
F major | F Gm Am Bb C Dm Edim
F# major | F# G#m A#m B C# D#m E#dim
Gb major | Gb Abm Bbm Cb Db Ebm Fdim
G major | G Am Bm C D Em F#dim
Ab major | Ab Bbm Cm Db Eb Fm Gdim
A major | A Bm C#m D E F#m G#dim
Bb major | Bb Cm Dm Eb F Gm Adim
B major | B C#m D#m E F# G#m A#dim
