Logistische regressieanalyse

De uitkomst in logistische regressieanalyse wordt vaak gecodeerd als 0 of 1, waarbij 1 aangeeft dat de uitkomst van belang aanwezig is, en 0 aangeeft dat de uitkomst van belang afwezig is. Als we p definiëren als de kans dat de uitkomst 1 is, kan het meervoudige logistische regressiemodel als volgt worden geschreven:

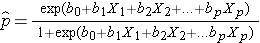
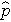is de verwachte kans dat de uitkomst aanwezig is; X1 tot en met Xp zijn afzonderlijke onafhankelijke variabelen; en b0 tot en met bp zijn de regressiecoëfficiënten. Het meervoudige logistische regressiemodel wordt soms anders geschreven. In de volgende vorm is de uitkomst de verwachte log van de kans dat de uitkomst aanwezig is,

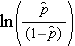
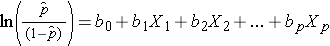
Merk op dat de rechterkant van de bovenstaande vergelijking lijkt op de meervoudige lineaire regressievergelijking. De techniek voor het schatten van de regressiecoëfficiënten in een logistisch regressiemodel is echter anders dan die voor het schatten van de regressiecoëfficiënten in een meervoudig lineair regressiemodel. Bij logistische regressie geven de uit het model afgeleide coëfficiënten (bv. b1) de verandering in de verwachte log-kans aan ten opzichte van een verandering van één eenheid in X1, waarbij alle andere voorspellers constant worden gehouden. Daarom levert de antilog van een geschatte regressiecoëfficiënt, exp(bi), een odds ratio op, zoals geïllustreerd in het onderstaande voorbeeld.

Voorbeeld van logistische regressie – associatie tussen obesitas en CVD

Wij hebben eerder gegevens geanalyseerd van een onderzoek dat was ontworpen om de associatie tussen obesitas (gedefinieerd als BMI > 30) en incidentele hart- en vaatziekten te beoordelen. Gegevens werden verzameld van deelnemers die tussen de 35 en 65 jaar oud waren, en vrij van hart- en vaatziekten (CVD) op baseline. Elke deelnemer werd gedurende 10 jaar gevolgd voor de ontwikkeling van hart- en vaatziekten. Een samenvatting van de gegevens is te vinden op pagina 2 van deze module. Het niet-gecorrigeerde of ruwe relatieve risico was RR = 1,78, en de niet-gecorrigeerde of ruwe odds ratio was OR =1,93. Wij stelden ook vast dat leeftijd een confounder was, en met behulp van de Cochran-Mantel-Haenszel methode, schatten wij een aangepast relatief risico van RRCMH =1,44 en een aangepaste odds ratio van ORCMH =1,52. We zullen nu logistische regressieanalyse gebruiken om de associatie tussen obesitas en incident cardiovasculaire ziekte te beoordelen, gecorrigeerd voor leeftijd.

Uit de logistische regressieanalyse komt het volgende naar voren:

Onafhankelijke variabele	Regressiecoëfficiënt	Chi-square	P-waarde
Intercept	-2.367	307.38	0.0001
Obesitas	0.658	9.87	0.0017

Het eenvoudige logistische regressiemodel relateert obesitas aan de logkans op incidenteel CVD:

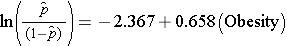
Obesitas is een indicatorvariabele in het model, als volgt gecodeerd: 1=obesitas en 0=niet obesitas. De log-kans op een incidenteel CVD is 0,658 maal hoger bij personen die zwaarlijvig zijn dan bij personen die niet zwaarlijvig zijn. Als we de antilog van de regressiecoëfficiënt nemen, exp(0,658) = 1,93, krijgen we de ruwe of niet-gecorrigeerde odds ratio. De kans op het ontwikkelen van CVD is 1,93 keer hoger bij zwaarlijvige personen in vergelijking met niet zwaarlijvige personen. Het verband tussen obesitas en het optreden van CVD is statistisch significant (p=0,0017). Merk op dat de teststatistieken om de significantie van de regressieparameters in logistische regressieanalyse te beoordelen gebaseerd zijn op chi-kwadraatstatistieken, in tegenstelling tot t-statistieken zoals het geval was bij lineaire regressieanalyse. Dit komt doordat een andere schattingstechniek, maximale waarschijnlijkheidsschatting genaamd, wordt gebruikt om de regressieparameters te schatten (zie Hosmer en Lemeshow3 voor technische details).

Veel statistische rekenpakketten genereren ook odds ratio’s, alsmede 95%-betrouwbaarheidsintervallen voor de odds ratio’s als onderdeel van hun logistische regressieanalyseprocedure. In dit voorbeeld is de schatting van de odds ratio 1,93 en het 95%-betrouwbaarheidsinterval is (1,281, 2,913).

Bij het onderzoek naar de associatie tussen obesitas en CVD hebben we eerder vastgesteld dat leeftijd een confounder was.Het volgende meervoudige logistische regressiemodel schat de associatie tussen obesitas en incident CVD, gecorrigeerd voor leeftijd. In het model beschouwen we opnieuw twee leeftijdsgroepen (minder dan 50 jaar en 50 jaar en ouder). Voor de analyse wordt de leeftijdsgroep als volgt gecodeerd: 1=50 jaar en ouder en 0=minder dan 50 jaar.

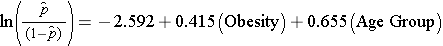
Als we de antilog nemen van de regressiecoëfficiënt die samenhangt met obesitas, exp(0,415) = 1,52, krijgen we de voor leeftijd gecorrigeerde odds ratio. De kans op het ontwikkelen van een CVD is, gecorrigeerd voor leeftijd, 1,52 maal zo groot bij personen met obesitas als bij personen zonder obesitas. In paragraaf 9.2 hebben we de Cochran-Mantel-Haenszel-methode gebruikt om een voor leeftijd gecorrigeerde odds ratio te genereren en het volgende gevonden:

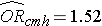
Dit illustreert hoe meervoudige logistische regressieanalyse kan worden gebruikt om rekening te houden met verstorende factoren. De modellen kunnen worden uitgebreid om rekening te houden met meerdere verstorende variabelen tegelijk. Meervoudige logistische regressieanalyse kan ook worden gebruikt om verwarring en effectmodificatie te beoordelen, en de benaderingen zijn identiek aan die welke in meervoudige lineaire regressieanalyse worden gebruikt. Meervoudige logistische regressieanalyse kan ook worden gebruikt om het effect van meerdere risicofactoren (in tegenstelling tot de focus op een enkele risicofactor) op een dichotome uitkomst te onderzoeken.

Voorbeeld – Risicofactoren geassocieerd met een laag geboortegewicht van de baby

Voorstel dat de onderzoekers zich ook bezighouden met nadelige zwangerschapsuitkomsten, waaronder zwangerschapsdiabetes, pre-eclampsie (d.w.z. zwangerschap-geïnduceerde hypertensie) en vroeggeboorte. Herinner u dat de studie 832 zwangere vrouwen betrof die demografische en klinische gegevens verstrekten. In de steekproef van de studie ontwikkelen 22 (2,7%) vrouwen pre-eclampsie, 35 (4,2%) zwangerschapsdiabetes en 40 (4,8%) vroeggeboorte. Stel dat we willen nagaan of er verschillen zijn in elk van deze nadelige zwangerschapsuitkomsten naar ras/etniciteit, gecorrigeerd voor de leeftijd van de moeder. Drie afzonderlijke logistische regressieanalyses werden uitgevoerd om elk resultaat afzonderlijk te relateren aan de 3 dummy- of indicatorvariabelen die het ras van de moeder en de leeftijd van de moeder, in jaren, weergeven. De resultaten staan hieronder.

0.0004 0.0004 0.0004 0.0004 0.0004.900 (0,286, 2,829)

.9046

Uitkomst: Pre-eclampsie	Regressiecoëfficiënt	Chi-square	P-waarde	Odds Ratio (95% CI)
Intercept	-3.066	4.518	0.0335	–
Zwart ras	2,191	12,640	0,0004	8.948 (2.673, 29.949)
Spaans ras	-0.1053	0.0325	0.8570	0.0004	0.0004
Ander ras	0,0586	0,0021	0,9046	0,8570	1,060 (0,104, 3,698)
Leeftijd van de moeder (jr.)	-0,0252	0.3574	0.5500	0.975 (0.898, 1.059)

Het enige statistisch significante verschil in pre-eclampsie is tussen zwarte en blanke moeders.

Zwarte moeders hebben bijna 9 keer meer kans om pre-eclampsie te ontwikkelen dan blanke moeders, gecorrigeerd voor de leeftijd van de moeder. Het 95%-betrouwbaarheidsinterval voor de odds ratio die zwarte versus blanke vrouwen vergelijkt die pre-eclampsie ontwikkelen, is zeer breed (2,673 tot 29,949). Dit is te wijten aan het feit dat er een klein aantal uitkomsten is (slechts 22 vrouwen ontwikkelen pre-eclampsie in de totale steekproef) en een klein aantal vrouwen van zwart ras in de studie. Deze associatie moet dus met de nodige voorzichtigheid worden geïnterpreteerd.

Hoewel de odds ratio statistisch significant is, suggereert het betrouwbaarheidsinterval dat de grootte van het effect kan variëren van een 2,6-voudige toename tot een 29,9-voudige toename. Een grotere studie is nodig om tot een nauwkeuriger schatting van het effect te komen.

Diabetes na de bevalling	Regressiecoëfficiënt	Chi-kwadraat	P-waarde	Odds Ratio (95% CI)
Intercept	-5.823	22.968	0.0001	–
Zwart ras	1.621	6.660	0.0099	5.056 (1.477, 17.312)
Hospaans ras	0.581	1.766	0.1839	1.787 (0.759, 4.207)
Ander ras	1.348	5.917	0.0150	3.848 (1.299, 11.395)
Leeftijd moeder (jr.)	0.071	4.314	0.0378	1.073 (1.004, 1.147)

Met betrekking tot zwangerschapsdiabetes zijn er statistisch significante verschillen tussen zwarte en blanke moeders (p=0.0099) en tussen moeders die zichzelf identificeren als ander ras in vergelijking met blank (p=0.0150), gecorrigeerd voor de leeftijd van de moeder. De leeftijd van de moeder is ook statistisch significant (p=0,0378), waarbij oudere vrouwen meer kans hebben om zwangerschapsdiabetes te ontwikkelen, gecorrigeerd voor ras/etniciteit.

.548

Outcome: Vroeggeboorte	Regressiecoëfficiënt	Chi-square	P-waarde	Odds Ratio (95% CI)
Intercept	-1.443	1.602	0.2056	–
Zwart ras	-0.082	0.015	0.9039	0.921 (0.244, 3.483)
Hispanic race	-1.564	9.497	0.0021	0.209 (0.077, 0.566)
ander ras	0.0021	0.209 (0.077, 0.566)
andere	1.124	0.2890	1.730 (0.628,4.767)
Leeftijd moeder (jrg.	00,037	1,198	0,2737	0,963 (0,901, 1,030)

Wat de voortijdige bevalling betreft, is het enige statistisch significante verschil tussen Latijns-Amerikaanse en blanke moeders (p=0,0021). Hispanic moeders hebben 80% minder kans op vroeggeboorte dan blanke moeders (odds ratio = 0.209), gecorrigeerd voor de leeftijd van de moeder.

Multivariabele methoden zijn rekenkundig complex en vereisen over het algemeen het gebruik van een statistisch rekenpakket. Multivariabele methoden kunnen worden gebruikt om confounding te beoordelen en hiervoor te corrigeren, om te bepalen of er sprake is van effect modificatie, of om de relaties van verschillende blootstellings- of risicofactoren op een uitkomst tegelijk te beoordelen. Multivariabele analyses zijn complex, en moeten altijd zo worden gepland dat ze biologisch plausibele verbanden weerspiegelen. Hoewel het relatief eenvoudig is om een extra variabele in aanmerking te nemen in een meervoudig lineair of meervoudig logistisch regressiemodel, mogen alleen variabelen worden opgenomen die klinisch zinvol zijn.

Het is belangrijk om te onthouden dat multivariabele modellen alleen kunnen aanpassen of rekening houden met verschillen in verstorende variabelen die in het onderzoek werden gemeten. Bovendien moeten multivariabele modellen alleen worden gebruikt om rekening te houden met confounding wanneer er enige overlap is in de verdeling van de confounder elk van de risicofactor groepen.

Gestratificeerde analyses zijn zeer informatief, maar als de steekproeven in specifieke strata te klein zijn, kunnen de analyses precisie missen. Bij het plannen van studies moeten onderzoekers zorgvuldig aandacht besteden aan potentiële effectmodificatoren. Als het vermoeden bestaat dat een verband tussen een blootstelling of een risicofactor in specifieke groepen anders is, moet het onderzoek zo worden opgezet dat er in elk van die groepen voldoende deelnemers zijn. Aan de hand van formules voor de steekproefgrootte moet worden bepaald hoeveel proefpersonen in elk stratum nodig zijn om te zorgen voor voldoende precisie of power bij de analyse.

terug naar boven | vorige pagina | volgende pagina