Eenvoudige beschrijving
Laten we eerst de pi binding in etheen bekijken vanuit een vereenvoudigd MO theorie standpunt (in dit voorbeeld laten we de sigma bindingen in het molecuul buiten beschouwing, en denken we alleen aan de π binding). We beginnen met twee atomaire banen: een ongebrugde 2p baan van elke koolstof. Elk bevat een enkel elektron. In de MO theorie combineren de twee atomaire banen zich wiskundig tot twee pi moleculaire banen, een laag-energetische pi bindingsbaan en een hoog-energetische pi* anti-bindingsbaan.

Moleculaire banen voor etheen (ethyleen)
In de bindende pi orbitaal hebben de twee gearceerde lobben van de p orbitalen een constructieve interactie met elkaar, net als de twee niet-gearceerde lobben (vergeet niet dat de willekeurige keuze van arcering wiskundige (+) en (-) tekens voorstelt voor de wiskundige golffunctie die de orbitaal beschrijft). Er is een verhoogde elektronendichtheid tussen de twee koolstofkernen in de moleculaire orbitaal – het is een bindingsinteractie.
In de hogere-energie anti-bonding pi* orbitaal interageert de gearceerde lob van de ene p orbitaal destructief met de niet-gearceerde lob van de tweede p orbitaal, wat leidt tot een knoop tussen de twee kernen en een algemene afstoting tussen de koolstofkernen.
Opnieuw gebruikmakend van het ‘opbouw’-principe, plaatsen we de twee elektronen in de laagenergetische, bindende pi moleculaire orbitaal. De anti-bindende pi* orbitaal blijft leeg.
Meer gedetailleerde MO beschrijving van etheen
Moleculaire orbitaaltheorie is met veel succes toegepast op grote geconjugeerde systemen, vooral die met ketens van koolstofatomen met afwisselend enkele en dubbele bindingen. Een benadering die door Hückel in 1931 werd geïntroduceerd, beschouwt alleen de gedelokaliseerde p-elektronen die bewegen in een raamwerk van \pi -bindingen. Dit is in feite een meer verfijnde versie van een vrije-elektronenmodel. Voor een inleidende cursus organische chemie hoeven we niet alle wiskunde van Hückel te gebruiken, maar voor degenen die dieper willen graven, wordt hier een meer gedetailleerde analyse gegeven.
De eenvoudigste te beschouwen koolwaterstof met pi-bindingen is etheen (ethyleen), dat is opgebouwd uit vier waterstofatomen en twee koolstofatomen. Experimenteel weten we dat de H-C-H en H-C-C hoeken in etheen ongeveer 120° zijn. Deze hoek suggereert dat de koolstofatomen sp2 gehybridiseerd zijn, wat betekent dat een enkel bezette sp2 orbitaal op één koolstof overlapt met een enkel bezette s orbitaal op elke H en een enkel bezette sp2 lob op de andere C. Zo vormt elke koolstof een set van drie σ-bindingen: twee C-H (sp2 + s) en één C-C (sp2 + sp2) (deel (a) van figuur 13.1. hieronder).

Figuur 13.1. (a) Het σ-gebonden kader wordt gevormd door de overlapping van twee sets enkel bezette koolstof-sp2-hybride orbitalen en vier enkel bezette waterstof-1s orbitalen om elektronenpaarbindingen te vormen. Hierbij worden 10 van de 12 valentie-elektronen gebruikt om in totaal vijf σ-bindingen te vormen (vier C-H-bindingen en één C-C-binding). (b) Eén enkel bezette ongebrugde 2pz orbitaal blijft over op elk koolstofatoom om een koolstof-kool π binding te vormen. (Opmerking: volgens afspraak is bij planaire moleculen de as loodrecht op het molecuulvlak de z-as.)
De Hückel-benadering wordt gebruikt om de energieën en de vormen van de piramoleculaire banen in geconjugeerde systemen te bepalen. Binnen de Hückel-benadering kunnen de covalente bindingen in deze koolwaterstoffen worden gescheiden in twee onafhankelijke “raamwerken”: het \sigma-bindingsraamwerk en het \sigma-bindingsraamwerk. De golffuncties die worden gebruikt om de bindingsbanen in elk raamwerk te beschrijven zijn het resultaat van verschillende combinaties van atomaire orbitalen. De methode beperkt zich tot geconjugeerde koolwaterstoffen en in het bijzonder worden alleen de sigma-elektronen in de moleculaire banen opgenomen, omdat deze de algemene eigenschappen van deze moleculen bepalen; de sigma-elektronen worden genegeerd. Dit wordt sigma-pi scheidbaarheid genoemd en wordt gerechtvaardigd door de orthogonaliteit van sigma- en pi-elektronen in planaire moleculen. Om deze reden is de Hückel methode beperkt tot planaire systemen. De Hückel benadering gaat ervan uit dat de elektronen in de \pi bindingen een elektrostatische potentiaal “voelen” die wordt veroorzaakt door het gehele \sigma bindingskader in het molecuul (d.w.z. het richt zich alleen op de vorming van \pi bindingen, gegeven dat het \sigma bindingskader al is gevormd).
Geconjugeerde systemen
Een geconjugeerd systeem heeft een gebied van overlappende p-orbitalen, die de tussenliggende enkelvoudige bindingen overbruggen, die een delokalisatie van pi-elektronen over alle aangrenzende uitgelijnde p-orbitalen mogelijk maken. Deze elektronen behoren niet tot een enkele binding of atoom, maar eerder tot een groep atomen.
Etheen
Voordat we de Hückel-behandeling voor etheen bekijken, is het nuttig om het algemene bindingsbeeld van het molecuul te bekijken. De binding in etheen bestaat uit de sp^2 hybridisatie van de 2s , 2p_x , en 2p_y atomaire banen op elk koolstofatoom, waarbij de 2p_z banen onaangeroerd blijven (figuur 13.2).
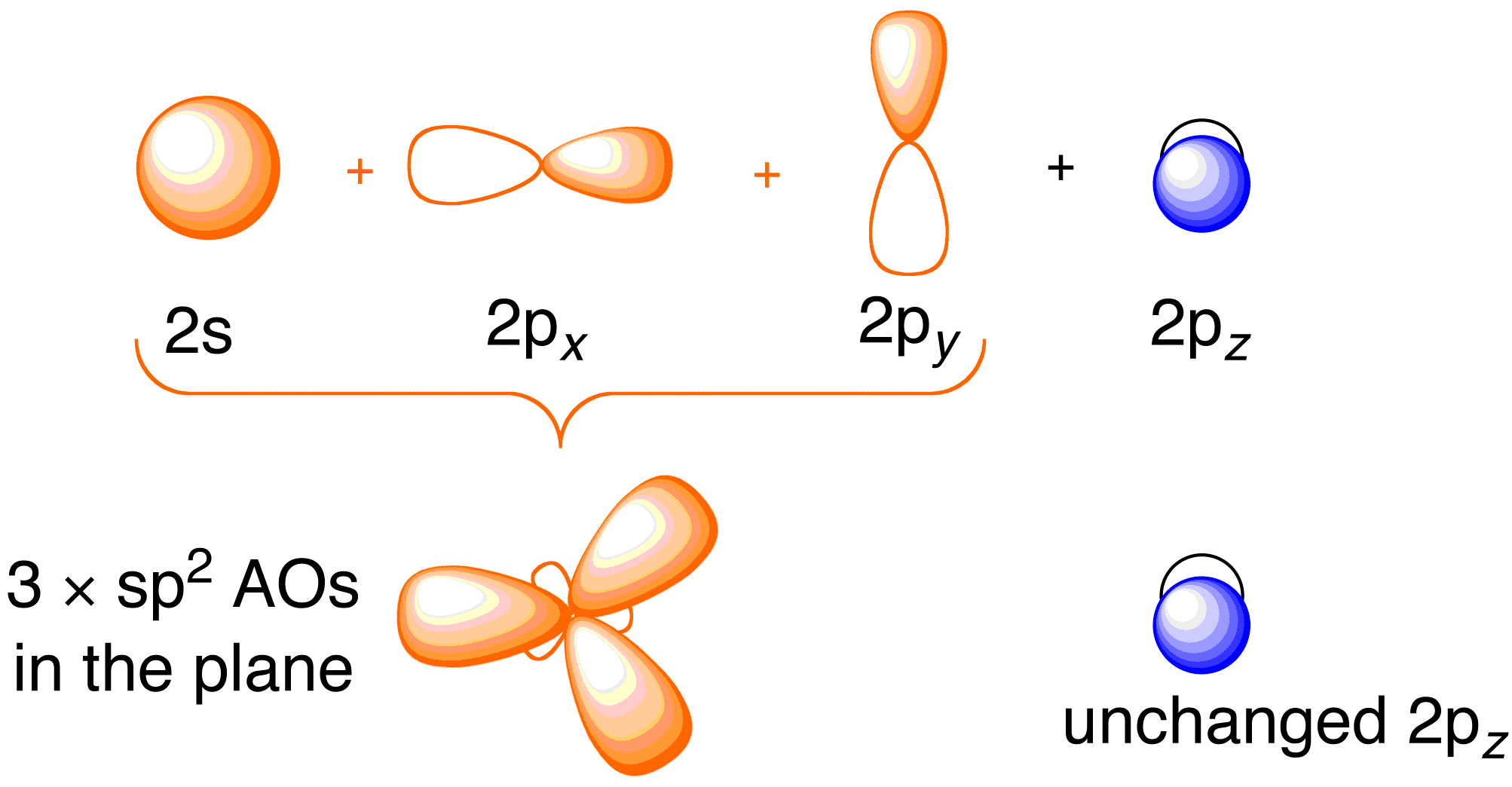
Figuur 13.2. Hybridisatie van de koolstofatomaire banen om sp^2 hybride banen te verkrijgen voor binding aan waterstofatomen in etheen. Afbeelding gebruikt met toestemming van ChemTube (CC-SA-BY-NC; Nick Greeves).
Het gebruik van hybride orbitalen in de hier beschreven moleculaire orbitaalbenadering is slechts een gemak en er wordt niet (direct) een beroep gedaan op de valentiebindingstheorie. Een identieke beschrijving kan worden verkregen door uitsluitend atomaire banen op koolstof te gebruiken, maar de interpretatie van de resulterende golffuncties is minder intuïtief. Bijvoorbeeld, de i-de moleculaire orbitaal kan worden beschreven via hybride orbitalen
of via atomaire orbitalen.
waarbij {a_i} en {c_i} coëfficiënten van de expansie zijn. Beide beschrijvingen werken en beide zijn identieke benaderingen omdat
waarin {c_i} coëfficiënten zijn die de gehybridiseerde orbitaal beschrijven.
De binding gebeurt via de vermenging van de elektronen in de sp^2 hybride banen op koolstof en de elektronen in de 1s atomaire banen van de vier waterstofatomen (figuur 13.2. linksboven), resulterend in het \pi – bindingsraamwerk. Het ipsi-bindingskader resulteert uit de ongebrugde 2p_z orbitalen (figuur 13.2. rechtsboven). De onafhankelijkheid van deze twee raamwerken blijkt uit het resulterende moleculaire orbitaaldiagram in onderstaande figuur; de Hückel-theorie houdt zich alleen bezig met de beschrijving van de moleculaire orbitalen en energieën van het ypi-bindingsraamwerk.

Figuur 13.3: Moleculaire orbitalen die de sigma-pi-scheidbaarheid aantonen van het \pi-bindingsraamwerk (blauw) en de \sigma-bindingsraamwerken (rood) van ethyleen.
De Hückel-behandeling heeft alleen betrekking op de beschrijving van de moleculaire orbitalen en energieën van het ¹piº-verbindingsraamwerk.
Aangezien de Hückel-theorie een speciale beschouwing is van de moleculaire orbitaaltheorie, kunnen de moleculaire orbitalen worden beschreven als een lineaire combinatie van de 2p_z atomaire orbitalen \phi op koolstof met hun bijbehorende coëfficiënten \c_i\}:
Voor de volledige kwantumchemische analyse met behulp van de Schrödingervergelijking (niet vereist voor de cursus organische chemie), zie deze Libretexts-pagina.
Deze moleculaire banen vormen het π-bindingsraamwerk en aangezien elke koolstof één elektron aan dit raamwerk bijdraagt, is alleen de laagste moleculaire baan ( | \psi_1 \rangle ) bezet (figuur ) in de grondtoestand. De bijbehorende elektronenconfiguratie is dan \pi_1^2 .

Figuur 13.4: Schematische voorstelling van het raamwerk van moleculaire orbitalen voor ethyleen. Merk op dat de antibonding-molecuulbaan één knoop meer heeft dan de binding-molecuulbaan, zoals verwacht omdat deze een hogere energie heeft.
HOMO en LUMO zijn acroniemen voor respectievelijk hoogst bezette molecuulbaan en laagst niet-bezette molecuulbaan, en worden vaak grensbanen genoemd. Het energieverschil tussen de HOMO en de LUMO wordt de HOMO-LUMO kloof genoemd.
De berekende 3-D pi molecuulbanen zijn weergegeven in figuur 13.5.

Figuur 13.5: Berekende 3-D pi molecuulbanen voor ethyleen. (links) de bindende orbitaal (ψ1) en (rechts) de antibindende (ψ2) orbitaal.
Bijdragers
- Seymour Blinder (emeritus hoogleraar scheikunde en natuurkunde aan de universiteit van Michigan, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
