In een normale verdeling zijn de gegevens symmetrisch verdeeld zonder scheefheid. Wanneer de gegevens in een grafiek worden uitgezet, volgen ze een klokvorm, waarbij de meeste waarden rond een centraal gebied zijn gegroepeerd en afnemen naarmate ze verder van het centrum af liggen.
Normale verdelingen worden vanwege hun vorm ook wel Gaussische verdelingen of klokvormige curven genoemd.

- Waarom zijn normale verdelingen belangrijk?
- Wat zijn de eigenschappen van normale verdelingen?
- Wat is uw plagiaatscore?
- Empirische regel
- Centrale limiet stelling
- Formule van de normale curve
- Wat is de standaardnormale verdeling?
- Om de waarschijnlijkheid te vinden met behulp van de z-verdeling
- Veelgestelde vragen over normale verdelingen
Waarom zijn normale verdelingen belangrijk?
Alle soorten variabelen in de natuur- en sociale wetenschappen zijn normaal of ongeveer normaal verdeeld. Lengte, geboortegewicht, leesvaardigheid, arbeidstevredenheid of SAT-scores zijn slechts enkele voorbeelden van dergelijke variabelen.
Omdat normaal verdeelde variabelen zo gewoon zijn, zijn veel statistische tests ontworpen voor normaal verdeelde populaties.
Inzicht in de eigenschappen van normale verdelingen betekent dat u inferentiële statistiek kunt gebruiken om verschillende groepen te vergelijken en schattingen te maken over populaties met behulp van steekproeven.
Wat zijn de eigenschappen van normale verdelingen?
Normale verdelingen hebben belangrijke kenmerken die gemakkelijk te zien zijn in grafieken:
- Het gemiddelde, de mediaan en de modus zijn precies hetzelfde.
- De verdeling is symmetrisch rond het gemiddelde – de helft van de waarden valt onder het gemiddelde en de helft erboven.
- De verdeling kan worden beschreven door twee waarden: het gemiddelde en de standaardafwijking.


Het gemiddelde is de plaatsbepalingsparameter, terwijl de standaardafwijking de schaalbepalingsparameter is.
Het gemiddelde bepaalt waar de piek van de kromme is gecentreerd. Door het gemiddelde te verhogen wordt de kromme naar rechts verplaatst, terwijl door het te verlagen de kromme naar links wordt verplaatst.


De standaardafwijking rekt de kromme uit of knijpt hem af. Een kleine standaardafwijking leidt tot een smalle kromme, terwijl een grote standaardafwijking tot een brede kromme leidt.


Empirische regel
De empirische regel, of de 68-95-99.7-regel, vertelt u waar de meeste waarden in een normale verdeling liggen:
- Rond 68% van de waarden ligt binnen 1 standaardafwijking van het gemiddelde.
- Rond 95% van de waarden ligt binnen 2 standaardafwijkingen van het gemiddelde.
- Rond 99,7% van de waarden ligt binnen 3 standaardafwijkingen van het gemiddelde.
Volgens de empirische regel:
- Rond 68% van de scores ligt tussen 1000 en 1300, 1 standaardafwijking boven en onder het gemiddelde.
- Rond 95% van de scores ligt tussen 850 en 1450, 2 standaarddeviaties boven en onder het gemiddelde.
- Rond 99,7% van de scores ligt tussen 700 en 1600, 3 standaarddeviaties boven en onder het gemiddelde.


De empirische regel is een snelle manier om een overzicht van uw gegevens te krijgen en te controleren of er uitschieters of extreme waarden zijn die dit patroon niet volgen.
Als gegevens uit kleine steekproeven dit patroon niet goed volgen, zijn andere verdelingen, zoals de t-verdeling, wellicht geschikter. Zodra u de verdeling van uw variabele hebt vastgesteld, kunt u geschikte statistische tests toepassen.
Centrale limiet stelling
De centrale limiet stelling is de basis voor hoe normale verdelingen werken in de statistiek.
In onderzoek, om een goed idee te krijgen van een populatiegemiddelde, zou u idealiter gegevens verzamelen van meerdere willekeurige steekproeven binnen de populatie. Een steekproefverdeling van het gemiddelde is de verdeling van de gemiddelden van deze verschillende steekproeven.
De centrale limiet stelling laat het volgende zien:
- Wet van Grote Aantallen: Naarmate je de steekproefgrootte (of het aantal steekproeven) vergroot, dan zal het steekproefgemiddelde het populatiegemiddelde benaderen.
- Met meerdere grote steekproeven is de steekproefverdeling van het gemiddelde normaal verdeeld, zelfs als je oorspronkelijke variabele niet normaal verdeeld is.
Parametrische statistische tests gaan er gewoonlijk van uit dat monsters afkomstig zijn van normaal verdeelde populaties, maar de centrale limiettheorema betekent dat aan deze aanname niet hoeft te worden voldaan als je een steekproef hebt die groot genoeg is.
Je kunt parametrische tests gebruiken voor grote steekproeven uit populaties met elke soort verdeling, zolang aan andere belangrijke aannames wordt voldaan. Een steekproefgrootte van 30 of meer wordt over het algemeen als groot beschouwd.
Voor kleine steekproeven is de aanname van normaliteit belangrijk omdat de steekproefverdeling van het gemiddelde niet bekend is. Voor nauwkeurige resultaten moet u er zeker van zijn dat de populatie normaal verdeeld is voordat u parametrische tests met kleine steekproeven kunt gebruiken.
Formule van de normale curve
Als u eenmaal het gemiddelde en de standaardafwijking van een normale verdeling hebt, kunt u een normale curve op uw gegevens passen met behulp van een waarschijnlijkheidsdichtheidsfunctie.


In een waarschijnlijkheidsdichtheidsfunctie vertelt het gebied onder de kromme u wat de waarschijnlijkheid is. De normale verdeling is een kansverdeling, dus het totale gebied onder de curve is altijd 1 of 100%.
De formule voor de normale kansdichtheidsfunctie ziet er tamelijk ingewikkeld uit. Maar om hem te gebruiken, hoeft u alleen het populatiegemiddelde en de standaardafwijking te kennen.
Voor elke waarde van x kunt u het gemiddelde en de standaardafwijking in de formule invoeren om de kansdichtheid te vinden van de variabele die die waarde van x aanneemt.
| Normale kansdichtheidsformule | Uitleg |
|---|---|
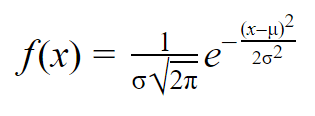 |
|
Op uw grafiek van de kansdichtheidsfunctie is de kans het gearceerde gebied onder de kromme dat rechts ligt van waar uw SAT-scores gelijk zijn aan 1380.


Je kunt de kanswaarde van deze score vinden met behulp van de standaardnormale verdeling.
Wat is de standaardnormale verdeling?
De standaardnormale verdeling, ook wel de z-verdeling genoemd, is een speciale normale verdeling waarbij het gemiddelde 0 is en de standaardafwijking 1.
Elke normale verdeling is een versie van de standaardnormale verdeling die is uitgerekt of samengeknepen en horizontaal naar rechts of naar links is verschoven.


Terwijl individuele waarnemingen uit normale verdelingen worden aangeduid als x, worden ze in de z-verdeling aangeduid als z. Elke normale verdeling kan worden omgezet in de standaardnormale verdeling door de afzonderlijke waarden om te zetten in z-scores.
Z-scores geven aan hoeveel standaardafwijkingen van het gemiddelde elke waarde ligt.


U hoeft alleen het gemiddelde en de standaardafwijking van uw verdeling te kennen om de z-score van een waarde te vinden.
| Formule Z-score | Uitleg |
|---|---|
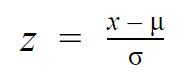 |
|
We zetten normale verdelingen om in de standaardnormale verdeling om verschillende redenen:
- Om de kans te vinden dat waarnemingen in een verdeling boven of onder een bepaalde waarde vallen.
- Om de waarschijnlijkheid te vinden dat een steekproefgemiddelde significant verschilt van een bekend populatiegemiddelde.
- Om scores op verschillende verdelingen met verschillende gemiddelden en standaardafwijkingen te vergelijken.
Om de waarschijnlijkheid te vinden met behulp van de z-verdeling
Elke z-score is geassocieerd met een waarschijnlijkheid, of p-waarde, die u vertelt hoe groot de kans is dat waarden onder die z-score zich voordoen. Als u een individuele waarde omzet in een z-score, kunt u vervolgens de waarschijnlijkheid vinden dat alle waarden tot die waarde voorkomen in een normale verdeling.
Het gemiddelde van onze verdeling is 1150, en de standaardafwijking is 150. De z-score vertelt je hoeveel standaardafwijkingen 1380 van het gemiddelde verwijderd is.
| Formule | Berekening |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
Voor een z-score van 1,53 is de p-waarde 0,937. Dit is de kans dat de SAT-score 1380 of lager is (93,7%), en het is het gebied onder de curve links van het gearceerde gebied.


Om het gearceerde gebied te vinden, neemt u 0.937 af van 1, dat is het totale gebied onder de kromme.
Kans van x>1380 = 1 – 0.937 = 0.063
Dat betekent dat het waarschijnlijk is dat slechts 6.3% van de SAT-scores in uw steekproef hoger is dan 1380.
Veelgestelde vragen over normale verdelingen
Bij een normale verdeling zijn de gegevens symmetrisch verdeeld zonder scheefheid. De meeste waarden groeperen zich rond een centraal gebied, waarbij de waarden afnemen naarmate ze verder van het centrum af liggen.
De maten van centrale tendens (gemiddelde, modus en mediaan) zijn bij een normale verdeling precies gelijk.
De standaardnormale verdeling, ook wel de z-verdeling genoemd, is een speciale normale verdeling waarbij het gemiddelde 0 is en de standaardafwijking 1.
Elke normale verdeling kan worden omgezet in de standaardnormale verdeling door de afzonderlijke waarden in z-scores te veranderen. In een z-verdeling vertellen z-scores hoeveel standaardafwijkingen elke waarde van het gemiddelde afligt.
De empirische regel, of de 68-95-99,7-regel, vertelt je waar de meeste waarden liggen in een normale verdeling:
- Rond 68% van de waarden ligt binnen 1 standaardafwijking van het gemiddelde.
- Rond 95% van de waarden ligt binnen 2 standaardafwijkingen van het gemiddelde.
- Rond 99,7% van de waarden ligt binnen 3 standaardafwijkingen van het gemiddelde.
De empirische regel is een snelle manier om een overzicht van uw gegevens te krijgen en te controleren op eventuele uitschieters of extreme waarden die dit patroon niet volgen.
De t-verdeling is een manier om een reeks waarnemingen te beschrijven waarbij de meeste waarnemingen dicht bij het gemiddelde vallen, en de rest van de waarnemingen de staarten aan weerszijden vormen. Het is een type normale verdeling dat wordt gebruikt voor kleinere steekproeven, waarbij de variantie in de gegevens onbekend is.
De t-verdeling vormt een klokcurve wanneer deze op een grafiek wordt uitgezet. Zij kan wiskundig worden beschreven met behulp van het gemiddelde en de standaardafwijking.

