Wynik w analizie regresji logistycznej jest często kodowany jako 0 lub 1, gdzie 1 oznacza, że wynik zainteresowania jest obecny, a 0 oznacza, że wynik zainteresowania jest nieobecny. Jeśli zdefiniujemy p jako prawdopodobieństwo, że wynik jest 1, model wielokrotnej regresji logistycznej można zapisać w następujący sposób:
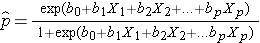
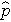jest oczekiwanym prawdopodobieństwem, że wynik jest obecny; X1 do Xp są odrębnymi zmiennymi niezależnymi; a b0 do bp są współczynnikami regresji. Model wielokrotnej regresji logistycznej jest czasami zapisywany w inny sposób. W następującej formie, wynik jest oczekiwanym logiem prawdopodobieństwa, że wynik jest obecny,
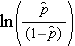
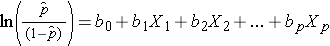
Zauważ, że prawa strona powyższego równania wygląda jak równanie wielokrotnej regresji liniowej. Jednak technika szacowania współczynników regresji w modelu regresji logistycznej różni się od techniki stosowanej do szacowania współczynników regresji w modelu wielokrotnej regresji liniowej. W regresji logistycznej współczynniki uzyskane z modelu (np. b1) wskazują zmianę oczekiwanych szans logarytmicznych w stosunku do zmiany X1 o jedną jednostkę, przy zachowaniu wszystkich innych predyktorów na stałym poziomie. Dlatego antylogarytm oszacowanego współczynnika regresji, exp(bi), daje iloraz szans, jak pokazano w poniższym przykładzie.
Przykład regresji logistycznej – związek między otyłością a chorobą sercowo-naczyniową
Wcześniej analizowaliśmy dane z badania mającego na celu ocenę związku między otyłością (zdefiniowaną jako BMI > 30) a występowaniem choroby sercowo-naczyniowej. Dane zostały zebrane od uczestników, którzy byli w wieku od 35 do 65 lat i byli wolni od choroby sercowo-naczyniowej (CVD) na początku badania. Każdy uczestnik był obserwowany przez 10 lat pod kątem rozwoju choroby sercowo-naczyniowej. Podsumowanie danych można znaleźć na stronie 2 niniejszego modułu. Nieskorygowane lub surowe ryzyko względne wynosiło RR = 1,78, a nieskorygowany lub surowy iloraz szans wynosił OR =1,93. Stwierdziliśmy również, że wiek jest czynnikiem zakłócającym, i używając metody Cochrana-Mantela-Haenszela, oszacowaliśmy skorygowane ryzyko względne RRCMH =1,44 i skorygowany iloraz szans ORCMH =1,52. Teraz użyjemy analizy regresji logistycznej, aby ocenić związek między otyłością a incydentem choroby sercowo-naczyniowej dostosowując się do wieku.
Analiza regresji logistycznej ujawnia następujące elementy:
|
Zmienna niezależna |
Współczynnik regresji |
Chi-kwadrat |
Wartość P |
|---|---|---|---|
|
Intercept |
-2.367 |
307.38 |
0.0001 |
|
Obesity |
0,658 |
9,87 |
0.0017 |
Prosty model regresji logistycznej wiąże otyłość z log odds of incident CVD:
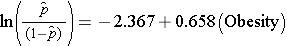
Otyłość jest w modelu zmienną wskaźnikową, kodowaną następująco: 1=otyły i 0=nie otyły. Log odds of incident CVD jest 0,658 razy wyższy u osób otyłych w porównaniu do osób nieotyłych. Jeśli weźmiemy antylog współczynnika regresji, exp(0,658) = 1,93, otrzymamy surowy lub nieskorygowany iloraz szans. Prawdopodobieństwo rozwoju CVD jest 1,93 razy większe u osób otyłych w porównaniu do osób nieotyłych. Związek między otyłością a incydentem CVD jest istotny statystycznie (p=0,0017). Zwróćmy uwagę, że statystyki testowe do oceny istotności parametrów regresji w analizie regresji logistycznej oparte są na statystyce chi kwadrat, w przeciwieństwie do statystyki t, jak to miało miejsce w przypadku analizy regresji liniowej. Dzieje się tak dlatego, że do oszacowania parametrów regresji stosowana jest inna technika estymacji, zwana estymacją maksymalnej wiarygodności (patrz Hosmer i Lemeshow3 w celu uzyskania szczegółów technicznych).
Wiele statystycznych pakietów obliczeniowych generuje również współczynniki szans, jak również 95% przedziały ufności dla współczynników szans jako część ich procedury analizy regresji logistycznej. W tym przykładzie oszacowanie ilorazu szans wynosi 1,93, a 95% przedział ufności wynosi (1,281, 2,913).
Badając związek między otyłością a CVD, wcześniej ustaliliśmy, że wiek był czynnikiem zakłócającym.Poniższy model wielokrotnej regresji logistycznej szacuje związek między otyłością a incydentem CVD, dostosowując się do wieku. W modelu ponownie uwzględniamy dwie grupy wiekowe (mniej niż 50 lat oraz 50 lat i więcej). Na potrzeby analizy grupa wiekowa jest kodowana w następujący sposób: 1=50 lat i więcej oraz 0=mniej niż 50 lat.
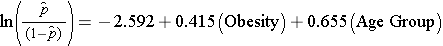
Jeśli weźmiemy antylog współczynnika regresji związanego z otyłością, exp(0,415) = 1,52 otrzymamy iloraz szans skorygowany o wiek. Prawdopodobieństwo rozwoju CVD jest 1,52 razy większe wśród osób otyłych w porównaniu z osobami nieotyłymi, przy uwzględnieniu wieku. W rozdziale 9.2 zastosowaliśmy metodę Cochrana-Mantela-Haenszela do wygenerowania ilorazu szans skorygowanego o wiek i uzyskaliśmy następujące wyniki:
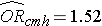
To ilustruje, w jaki sposób analiza wielokrotnej regresji logistycznej może być wykorzystana do uwzględnienia czynników zakłócających. The models can be extended to account for several confounding variables simultaneously. Analiza regresji logistycznej wielokrotnej może być również stosowana do oceny konfundacji i modyfikacji efektu, a podejścia są identyczne z tymi stosowanymi w analizie regresji liniowej wielokrotnej. Analiza wielokrotnej regresji logistycznej może być również stosowana do badania wpływu wielu czynników ryzyka (w przeciwieństwie do skupiania się na jednym czynniku ryzyka) na dychotomiczny wynik.
Przykład – Risk Factors Associated With Low Infant Birth Weight
Załóżmy, że badacze zajmują się również niekorzystnymi wynikami ciąży, w tym cukrzycą ciążową, stanem przedrzucawkowym (tj. nadciśnieniem indukowanym ciążą) i porodem przedwczesnym. Przypomnijmy, że w badaniu wzięły udział 832 ciężarne kobiety, które dostarczyły danych demograficznych i klinicznych. W badanej próbie u 22 (2,7%) kobiet wystąpił stan przedrzucawkowy, u 35 (4,2%) cukrzyca ciążowa, a u 40 (4,8%) poród przedwczesny. Załóżmy, że chcemy ocenić, czy istnieją różnice w każdym z tych niekorzystnych wyników ciąży według rasy/pochodzenia etnicznego, dostosowane do wieku matki. Trzy oddzielne analizy regresji logistycznej zostały przeprowadzone w odniesieniu do każdego wyniku, rozpatrywane oddzielnie, do 3 dummy lub zmiennych wskaźników odzwierciedlających rasę matki i wiek matki, w latach. Wyniki są poniżej.
|
Wynik: Stan przedrzucawkowy |
Współczynnik regresji |
Chi-square |
Wartość P |
Odds Ratio (95% CI) |
|---|---|---|---|---|
|
Intercept |
-3.066 |
4.518 |
0.0335 |
– |
|
Rasa czarna |
2,191 |
12,640 |
0,0004 |
8.948 (2,673, 29,949) |
|
Rasa hiszpańska |
-0,1053 |
0,0325 |
0,8570 |
0.900 (0,286, 2,829) |
|
Inna rasa |
0,0586 |
0,0021 |
0.9046 |
1,060 (0,104, 3,698) |
|
Wiek matki (yrs.) |
-0,0252 |
0.3574 |
0.5500 |
0.975 (0.898, 1.059) |
Jedyną istotną statystycznie różnicą w występowaniu stanu przedrzucawkowego jest różnica pomiędzy czarnymi i białymi matkami.
Czarne matki są prawie 9 razy bardziej narażone na wystąpienie stanu przedrzucawkowego niż białe matki, skorygowane o wiek matki. 95% przedział ufności dla ilorazu szans dla kobiet rasy czarnej i białej, u których wystąpił stan przedrzucawkowy jest bardzo szeroki (2,673 do 29,949). Wynika to z faktu małej liczby zdarzeń (tylko u 22 kobiet w całej próbie wystąpił stan przedrzucawkowy) i małej liczby kobiet rasy czarnej w badaniu. W związku z tym związek ten należy interpretować z ostrożnością.
Pomimo że iloraz szans jest statystycznie istotny, przedział ufności sugeruje, że wielkość efektu może wynosić od 2,6-krotnego wzrostu do 29,9-krotnego wzrostu. Aby uzyskać bardziej precyzyjne oszacowanie efektu, konieczne jest przeprowadzenie większego badania.
|
Cukrzyca ciążowa |
Współczynnik regresji |
Chi-square |
P-value |
Odds Ratio (95% CI) |
|---|---|---|---|---|
|
Intercept |
-5.823 |
22,968 |
0,0001 |
– |
|
Rasa czarna |
1,621 |
6.660 |
0,0099 |
5,056 (1,477, 17,312) |
|
Rasa hiszpańska |
0,581 |
1.766 |
0,1839 |
1,787 (0,759, 4,207) |
|
Inna rasa |
1,348 |
5.917 |
0,0150 |
3,848 (1,299, 11,395) |
|
Wiek matki (w latach) |
0,071 |
4.314 |
0,0378 |
1,073 (1,004, 1,147) |
W odniesieniu do cukrzycy ciążowej istnieją statystycznie istotne różnice między czarnymi i białymi matkami (p=0,0099) oraz między matkami identyfikującymi się jako innej rasy w porównaniu z białymi (p=0,0150), skorygowane o wiek matki. Wiek matki jest również istotny statystycznie (p=0,0378), przy czym starsze kobiety są bardziej narażone na wystąpienie cukrzycy ciążowej, skorygowane o rasę/pochodzenie etniczne.
|
Dochód: Preterm Labor |
Regression Coefficient |
Chi-square |
P-value |
Odds Ratio (95% CI) |
|---|---|---|---|---|
|
Intercept |
-1.443 |
1.602 |
0.2056 |
– |
|
Rasa czarna |
-0,082 |
0,015 |
0.9039 |
0,921 (0,244, 3,483) |
|
Rasa hiszpańska |
-1,564 |
9.497 |
0,0021 |
0,209 (0,077, 0,566) |
|
Inna rasa |
0.548 |
1,124 |
0,2890 |
1,730 (0,628,4,767) |
|
Wiek matki (yrs.) |
00,037 |
1,198 |
0,2737 |
0,963 (0,901, 1,030) |
W odniesieniu do porodu przed terminem, jedyna statystycznie istotna różnica występuje między matkami rasy latynoskiej i białej (p=0,0021). Latynoskie matki są o 80% mniej narażone na rozwój porodu przed terminem niż białe matki (iloraz szans = 0.209), dostosowane do wieku matki.
Metody wielozmiennowe są skomplikowane obliczeniowo i ogólnie wymagają użycia statystycznego pakietu obliczeniowego. Metody wielozmiennowe mogą być stosowane do oceny i korekty konfundacji, do określenia, czy istnieje modyfikacja efektu, lub do oceny zależności kilku czynników ekspozycji lub ryzyka na wynik jednocześnie. Analizy wielowariantowe są złożone i powinny być zawsze planowane tak, aby odzwierciedlały biologicznie wiarygodne zależności. Chociaż stosunkowo łatwo jest rozważyć dodatkową zmienną w modelu wielokrotnej regresji liniowej lub wielokrotnej regresji logistycznej, należy uwzględnić tylko te zmienne, które mają znaczenie kliniczne.
Ważne jest, aby pamiętać, że modele wielozmiennowe mogą jedynie korygować lub uwzględniać różnice w zmiennych zakłócających, które były mierzone w badaniu. Ponadto modele wielowariantowe powinny być stosowane do uwzględniania zmiennych zakłócających tylko wtedy, gdy rozkład zmiennych zakłócających w każdej z grup czynników ryzyka w pewnym stopniu się pokrywa.
Analizy stratyfikowane są bardzo pouczające, ale jeśli próbki w poszczególnych warstwach są zbyt małe, analizom może brakować precyzji. Planując badania, badacze muszą zwracać baczną uwagę na potencjalne modyfikatory efektu. Jeżeli istnieje podejrzenie, że związek między ekspozycją lub czynnikiem ryzyka jest inny w określonych grupach, to badanie musi być tak zaprojektowane, aby zapewnić wystarczającą liczbę uczestników w każdej z tych grup. Należy stosować wzory na wielkość próby w celu określenia liczby uczestników wymaganych w każdej warstwie, aby zapewnić odpowiednią precyzję lub moc analizy.
powrót do góry | poprzednia strona | następna strona