Prostszy opis
Rozważmy najpierw wiązanie pi w etenie z punktu widzenia uproszczonej teorii MO (w tym przykładzie będziemy pomijać wiązania sigma w cząsteczce i myśleć tylko o wiązaniu π). Zaczynamy od dwóch orbitali atomowych: po jednym niehybrydyzowanym orbitalu 2p z każdego węgla. Każdy z nich zawiera pojedynczy elektron. W teorii MO, te dwa atomowe łączą się matematycznie tworząc dwa orbitale pi molekularne, jeden niskoenergetyczny orbital wiążący pi i jeden wysokoenergetyczny orbital antyzwiązkowy pi*.

Orbitale molekularne dla etenu (etylenu)
W wiążącym orbitalu pi, dwa zacienione płaty orbitali p oddziałują konstruktywnie ze sobą, podobnie jak dwa niezacienione płaty (pamiętaj, arbitralny wybór cieniowania reprezentuje matematyczne (+) i (-) znaki dla matematycznej funkcji falowej opisującej orbital). Pomiędzy dwoma jądrami węgla w orbitalu molekularnym występuje zwiększona gęstość elektronów – jest to oddziaływanie wiążące.
W wyżejenergetycznym antyzwiązkowym orbitalu pi*, zacieniony płat jednego orbitalu p oddziałuje destrukcyjnie z niezacienionym płatem drugiego orbitalu p, prowadząc do powstania węzła pomiędzy dwoma jądrami i ogólnego odpychania pomiędzy jądrami węgla.
Ponownie używając zasady „budowania”, umieszczamy dwa elektrony w niżej energetycznym, wiążącym orbitalu molekularnym pi. Antywiązaniowy orbital pi* pozostaje pusty.
Szczegółowy opis MO etenu
Teoria orbitali molekularnych została z dużym powodzeniem zastosowana do dużych układów sprzężonych, szczególnie tych zawierających łańcuchy atomów węgla z naprzemiennie występującymi wiązaniami pojedynczymi i podwójnymi. Przybliżenie wprowadzone przez Hückla w 1931 r. uwzględnia tylko zdelokalizowane elektrony p poruszające się w ramach wiązań Δpi. Jest to w istocie bardziej wyrafinowana wersja modelu swobodnych elektronów. Dla wprowadzającego kursu chemii organicznej nie musimy używać całej matematyki Hückla, ale dla tych, którzy lubią wnikać głębiej, bardziej szczegółowa analiza jest podana tutaj.
Najprostszym węglowodorem do rozważenia, który wykazuje wiązanie \pi jest eten (etylen), który składa się z czterech atomów wodoru i dwóch atomów węgla. Doświadczalnie wiemy, że kąty H-C-H i H-C-C w etenie wynoszą około 120°. Kąt ten sugeruje, że atomy węgla są zhybrydyzowane sp2, co oznacza, że pojedynczo zajęty orbital sp2 na jednym węglu nakłada się z pojedynczo zajętym orbitalem s na każdym H i pojedynczo zajętym płatem sp2 na drugim C. Tak więc każdy węgiel tworzy zestaw trzech wiązań \sigma: dwa C-H (sp2 + s) i jedno C-C (sp2 + sp2) (część (a) rysunku 13.1. poniżej).

Rysunek 13.1. (a) Szkielet wiązania σ powstaje w wyniku nałożenia się dwóch zestawów pojedynczo zajętych orbitali hybrydowych sp2 węgla i czterech pojedynczo zajętych orbitali 1s wodoru w celu utworzenia wiązań elektronowo-parowych. Wykorzystuje to 10 z 12 elektronów walencyjnych do utworzenia w sumie pięciu wiązań σ (cztery wiązania C-H i jedno wiązanie C-C). (b) Jeden pojedynczo zajęty niehybrydyzowany orbital 2pz pozostaje na każdym atomie węgla tworząc wiązanie π węgiel-węgiel. (Uwaga: umownie, w cząsteczkach planarnych oś prostopadła do płaszczyzny molekularnej jest osią z.)
Przybliżenie Hückela jest używane do określenia energii i kształtów orbitali molekularnych w układach sprzężonych. W ramach przybliżenia Hückla, wiązanie kowalencyjne w tych węglowodorach może być rozdzielone na dwa niezależne „szkielety”: szkielet wiązania \sigma¨ i szkielet wiązania \sigma¨. Funkcje falowe używane do opisu orbitali wi±ż±cych w każdej z ram wynikaj± z różnych kombinacji orbitali atomowych. Metoda ogranicza się do węglowodorów sprzężonych i uwzględnia jedynie elektronowe orbitale molekularne, ponieważ to one określają ogólne właściwości tych cząsteczek; elektrony sigma są ignorowane. Jest to określane jako separowalność sigma-pi i jest uzasadnione ortogonalnością orbitali sigma i sigma-pi w cząsteczkach planarnych. Z tego powodu metoda Hückela jest ograniczona do układów planarnych. Aproksymacja Hückla zakłada, że elektrony w wiązaniach \”czują” potencjał elektrostatyczny wynikający z całego szkieletu wiązań \”sigma” w cząsteczce (tzn. skupia się tylko na tworzeniu wiązań \”sigma”, biorąc pod uwagę, że szkielet wiązań \”sigma” został już utworzony).
Układy skoniugowane
Układ skoniugowany posiada region nakładających się orbitali p, mostkujących przyległe wiązania pojedyncze, które pozwalają na delokalizację elektronów \pi przez wszystkie przyległe wyrównane orbitale p. Te elektrony \pi nie należą do pojedynczego wiązania lub atomu, ale raczej do grupy atomów.
Eten
Przed rozważeniem leczenia Hückela dla etenu, korzystne jest przejrzenie ogólnego obrazu wiązania w cząsteczce. Wiązanie w etenie polega na hybrydyzacji sp^2 orbitali atomowych 2s , 2p_x , i 2p_y na każdym atomie węgla; pozostawiając orbitale 2p_z nietknięte (Rysunek 13.2).
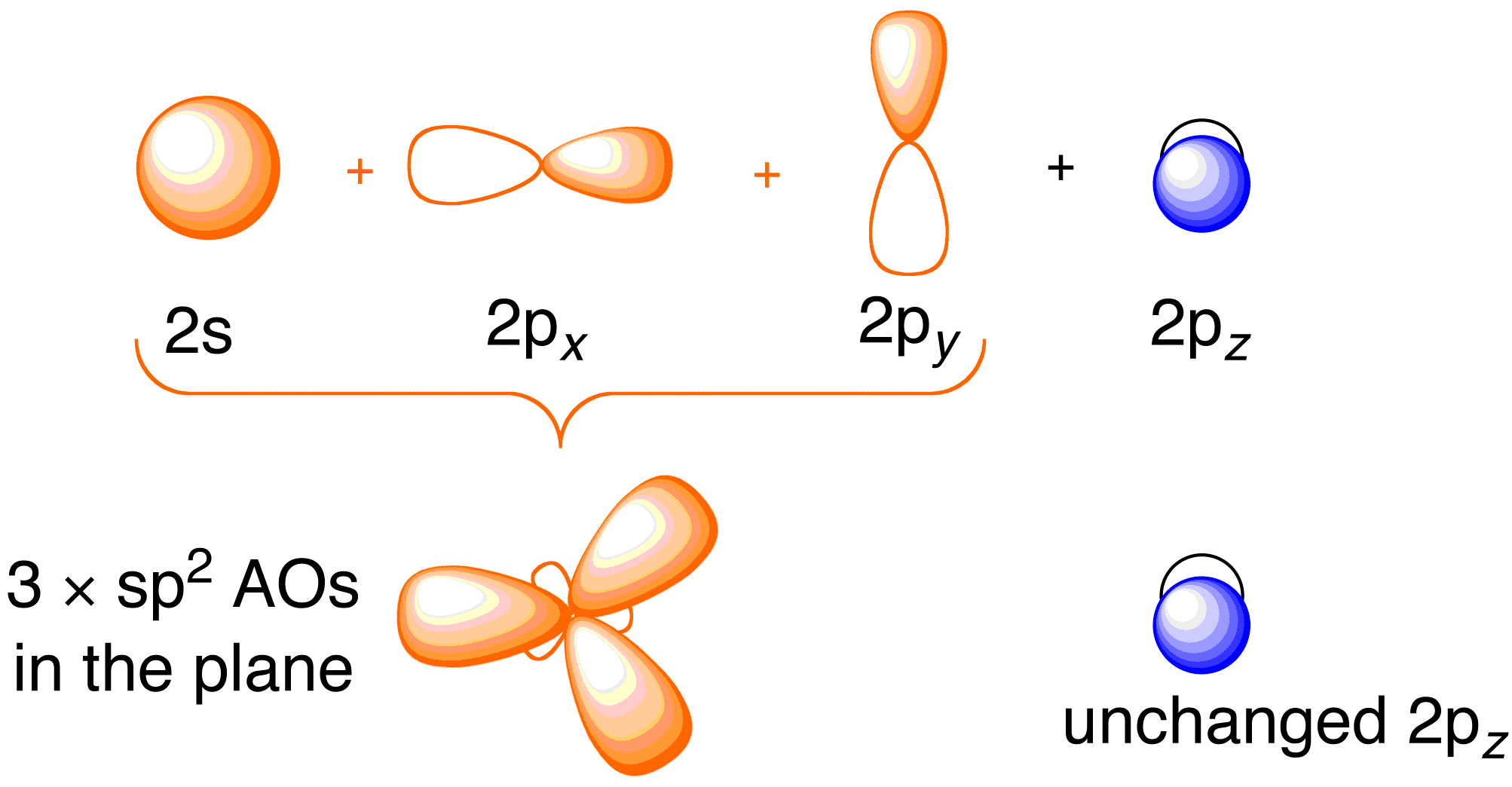
Rysunek 13.2. Hybrydyzacja orbitali atomu węgla w celu uzyskania orbitali hybrydowych sp^2 do wiązania z atomami wodoru w etenie. Obrazek użyty za zgodą ChemTube (CC-SA-BY-NC; Nick Greeves).
Użycie orbitali hybrydowych w opisywanym tu podejściu do orbitali molekularnych jest jedynie ułatwieniem i nie odwołuje się do teorii wiązań walencyjnych (bezpośrednio). Identyczny opis może być uzyskany przy użyciu wyłącznie orbitali atomowych na węglu, ale interpretacja wynikowych funkcji falowych jest mniej intuicyjna. Na przykład, i-ty orbital molekularny może być opisany poprzez orbitale hybrydowe
lub poprzez orbitale atomowe.
gdzie ∗ i ∗ są współczynnikami rozwinięcia. Każdy z tych opisów będzie działał i oba są identyczne, ponieważ
gdzie {c_i} są współczynnikami opisującymi zhybrydyzowany orbital.
Wiązanie zachodzi poprzez mieszanie elektronów na orbitalach hybrydowych sp^2 na węglu i elektronów na orbitalach atomowych 1s czterech atomów wodoru (Rysunek 13.2. powyżej po lewej), co skutkuje powstaniem struktury wiązania sigma. Ramy wiązania \P wynikają z niehybrydyzowanych orbitali 2p_z (Rysunek 13.2. powyżej, po prawej). Teoria Hückla zajmuje się tylko opisem orbitali molekularnych i energii ram wiązania ∗pi.

Rysunek 13.3: Orbitale molekularne wykazujące rozdzielność sigma-pi ram wiązania sigma-pi (niebieski) i sigma-wiązania (czerwony) etylenu.
Obróbka Hückela dotyczy tylko opisu orbitali molekularnych i energii ram wiązania \pi.
Ponieważ teoria Hückla jest specjalnym rozważaniem teorii orbitali molekularnych, orbitale molekularne | mogą być opisane jako liniowa kombinacja orbitali atomowych 2p_z \phi przy węglu z odpowiadającymi im współczynnikami \{c_i\}:
Aby uzyskać pełną analizę chemii kwantowej przy użyciu równania Schrödingera (nie wymaganą na zajęciach z chemii organicznej), zobacz tę stronę Libretexts.
Te orbitale molekularne tworzą szkielet wiązania π, a ponieważ każdy węgiel wnosi jeden elektron do tego szkieletu, tylko najniższy orbital molekularny ( | \psi_1 \rangle ) jest zajęty (Rysunek ) w stanie podstawowym. Odpowiadająca temu konfiguracja elektronowa wynosi zatem \pi_1^2 .

Rysunek 13.4: Schematyczne przedstawienie ram orbitali molekularnych dla etylenu . Zauważmy, że orbital molekularny przeciw wiązaniu ma jeden węzeł więcej niż orbital molekularny wiązania, zgodnie z oczekiwaniami, ponieważ ma wyższą energię.
HOMO i LUMO są akronimami dla najwyższego zajętego orbitalu molekularnego i najniższego nie zajętego orbitalu molekularnego, odpowiednio, i są często określane jako orbitale graniczne. Różnica energii pomiędzy HOMO i LUMO jest określana jako luka HOMO-LUMO.
Orbitale molekularne obliczone w układzie 3-D przedstawiono na rysunku 13.5.

Rysunek 13.5: Obliczone orbitale molekularne dla etylenu . (po lewej) orbital wiążący (ψ1) i (po prawej) orbital antyzwiązkowy (ψ2).
Współautorzy
- Seymour Blinder (emerytowany profesor chemii i fizyki na Uniwersytecie Michigan, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
.
