Trójkąt z jednym kątem prostym nazywamy trójkątem prostym. Bok przeciwległy do kąta prostego nazywamy przeciwprostokątną trójkąta. Pozostałe dwa boki są nazywane nogami. Pozostałe dwa kąty nie mają specjalnej nazwy, ale zawsze są komplementarne. Czy widzisz dlaczego? Całkowita suma kątów w trójkącie wynosi 180 stopni, a kąt prosty ma 90 stopni, więc pozostałe dwa muszą mieć sumę 90 stopni.
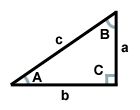
Powyższy trójkąt ma bok c jako przeciwprostokątną, boki a i b jako nogi, a kąt C jako kąt prosty. Kąty A i B są komplementarne.
Są dwa rodzaje trójkątów prostych, które każdy matematyk powinien znać bardzo dobrze. Jeden z nich to trójkąt prosty, który powstaje, gdy z wierzchołka trójkąta równobocznego poprowadzimy wysokość, tworząc dwa przystające trójkąty proste. Kąty trójkąta będą miały miary 30, 60 i 90 stopni, stąd nazwa trójkąta: trójkąt 30-60-90. Stosunek długości boków w takich trójkątach jest zawsze taki sam: jeśli noga przeciwległa do kąta 30 stopni ma długość x, noga przeciwległa do kąta 60 stopni będzie miała długość x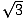
, a przeciwprostokątna leżąca naprzeciwko kąta prostego będzie miała długość 2x. Oto trójkąt 30-60-90 przedstawiony na rysunku poniżej.
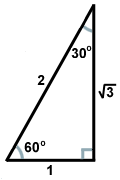
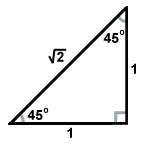
Inny popularny trójkąt prosty wynika z pary trójkątów powstałych, gdy przekątna dzieli kwadrat na dwa trójkąty. Każdy z tych trójkątów jest przystający i ma kąty o miarach 45, 45 i 90 stopni. Jeśli odnogi przeciwległych kątów 45 stopni mają długość x, to przeciwprostokątna ma długość x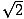
. Ten stosunek jest prawdziwy dla wszystkich trójkątów 45-45-90. Trójkąty 45-45-90 są również często nazywane trójkątami równoramiennymi prostokątnymi.
Jedną z ostatnich cech, na którą należy zwrócić uwagę jest to, że nogi trójkąta prostego są jednocześnie wysokościami trójkąta. Dlatego pole trójkąta prostokątnego jest równe połowie iloczynu długości jego nóg.