Descripción simple
Consideremos primero el enlace pi en el eteno desde un punto de vista simplificado de la teoría MO (en este ejemplo prescindiremos de los enlaces sigma en la molécula, y pensaremos sólo en el enlace π). Comenzamos con dos orbitales atómicos: un orbital 2p no hibridado de cada carbono. Cada uno contiene un solo electrón. En la teoría de la MO, los dos atómicos se combinan matemáticamente para formar dos orbitales moleculares pi, uno un orbital de enlace pi de baja energía y otro un orbital antienlace pi* de alta energía.

Orbitales moleculares para el eteno (etileno)
En el orbital pi de enlace, los dos lóbulos sombreados de los orbitales p interactúan constructivamente entre sí, al igual que los dos lóbulos no sombreados (recuerde que la elección arbitraria del sombreado representa los signos matemáticos (+) y (-) para la función de onda matemática que describe el orbital). Hay una mayor densidad de electrones entre los dos núcleos de carbono en el orbital molecular – es una interacción de enlace.
En el orbital pi* antienlace de mayor energía, el lóbulo sombreado de un orbital p interactúa destructivamente con el lóbulo no sombreado del segundo orbital p, dando lugar a un nodo entre los dos núcleos y a una repulsión general entre los núcleos de carbono.
Utilizando de nuevo el principio de «acumulación», colocamos los dos electrones en el orbital molecular pi de menor energía y de enlace. El orbital pi* antienlace permanece vacío.
Descripción MO más detallada del eteno
La teoría de orbitales moleculares se ha aplicado con mucho éxito a grandes sistemas conjugados, especialmente a los que contienen cadenas de átomos de carbono con enlaces simples y dobles alternados. Una aproximación introducida por Hückel en 1931 considera sólo los electrones p deslocalizados que se mueven en un marco de enlaces \pi. Esta es, de hecho, una versión más sofisticada de un modelo de electrones libres. Para un curso de introducción a la química orgánica no es necesario utilizar todas las matemáticas de Hückel, pero para aquellos que quieran profundizar, se ofrece aquí un análisis más detallado.
El hidrocarburo más sencillo de considerar que presenta enlaces \pi es el eteno (etileno), que está formado por cuatro átomos de hidrógeno y dos de carbono. Experimentalmente, sabemos que los ángulos H-C-H y H-C-C en el eteno son de aproximadamente 120°. Este ángulo sugiere que los átomos de carbono están hibridizados sp2, lo que significa que un orbital sp2 ocupado individualmente en un carbono se solapa con un orbital s ocupado individualmente en cada H y un lóbulo sp2 ocupado individualmente en el otro C. Así, cada carbono forma un conjunto de tres enlaces σ: dos C-H (sp2 + s) y un C-C (sp2 + sp2) (parte (a) de la Figura 13.1. siguiente).

Figura 13.1. (a) El entramado de enlaces σ está formado por la superposición de dos conjuntos de orbitales híbridos sp2 de carbono ocupados individualmente y cuatro orbitales 1s de hidrógeno ocupados individualmente para formar enlaces de pares de electrones. Esto utiliza 10 de los 12 electrones de valencia para formar un total de cinco enlaces σ (cuatro enlaces C-H y un enlace C-C). (b) En cada átomo de carbono queda un orbital 2pz no hibridado y ocupado individualmente para formar un enlace π carbono-carbono. (Nota: por convención, en las moléculas planas el eje perpendicular al plano molecular es el eje z.)
La aproximación de Hückel se utiliza para determinar las energías y formas de los orbitales moleculares \pi en los sistemas conjugados. Dentro de la aproximación de Hückel, el enlace covalente en estos hidrocarburos puede separarse en dos «marcos» independientes: el marco de enlace \sigma y el marco de enlace \sigma. Las funciones de onda utilizadas para describir los orbitales de enlace en cada marco son el resultado de diferentes combinaciones de orbitales atómicos. El método se limita a tratar los hidrocarburos conjugados y, en concreto, sólo se incluyen los orbitales moleculares de los electrones \i porque éstos determinan las propiedades generales de estas moléculas; los electrones sigma se ignoran. Esto se denomina separabilidad sigma-pi y se justifica por la ortogonalidad de los orbitales \sigma y \pi en las moléculas planas. Por esta razón, el método de Hückel se limita a sistemas planares. La aproximación de Hückel asume que los electrones en los enlaces \pi «sienten» un potencial electrostático debido a todo el marco de enlace \sigma en la molécula (es decir, se centra sólo en la formación de enlaces \pi, dado que el marco de enlace \sigma ya se ha formado).
Sistemas conjugados
Un sistema conjugado tiene una región de orbitales p superpuestos, que puentean los enlaces simples interyacentes, que permiten una deslocalización de electrones \pi a través de todos los orbitales p adyacentes alineados. Estos electrones \pi no pertenecen a un solo enlace o átomo, sino a un grupo de átomos.
Eteno
Antes de considerar el tratamiento de Hückel para el eteno, es beneficioso revisar la imagen general de enlace de la molécula. El enlace en el eteno implica la hibridación sp^2 de los orbitales atómicos 2s , 2p_x , y 2p_y en cada átomo de carbono; dejando intactos los orbitales 2p_z (Figura 13.2).
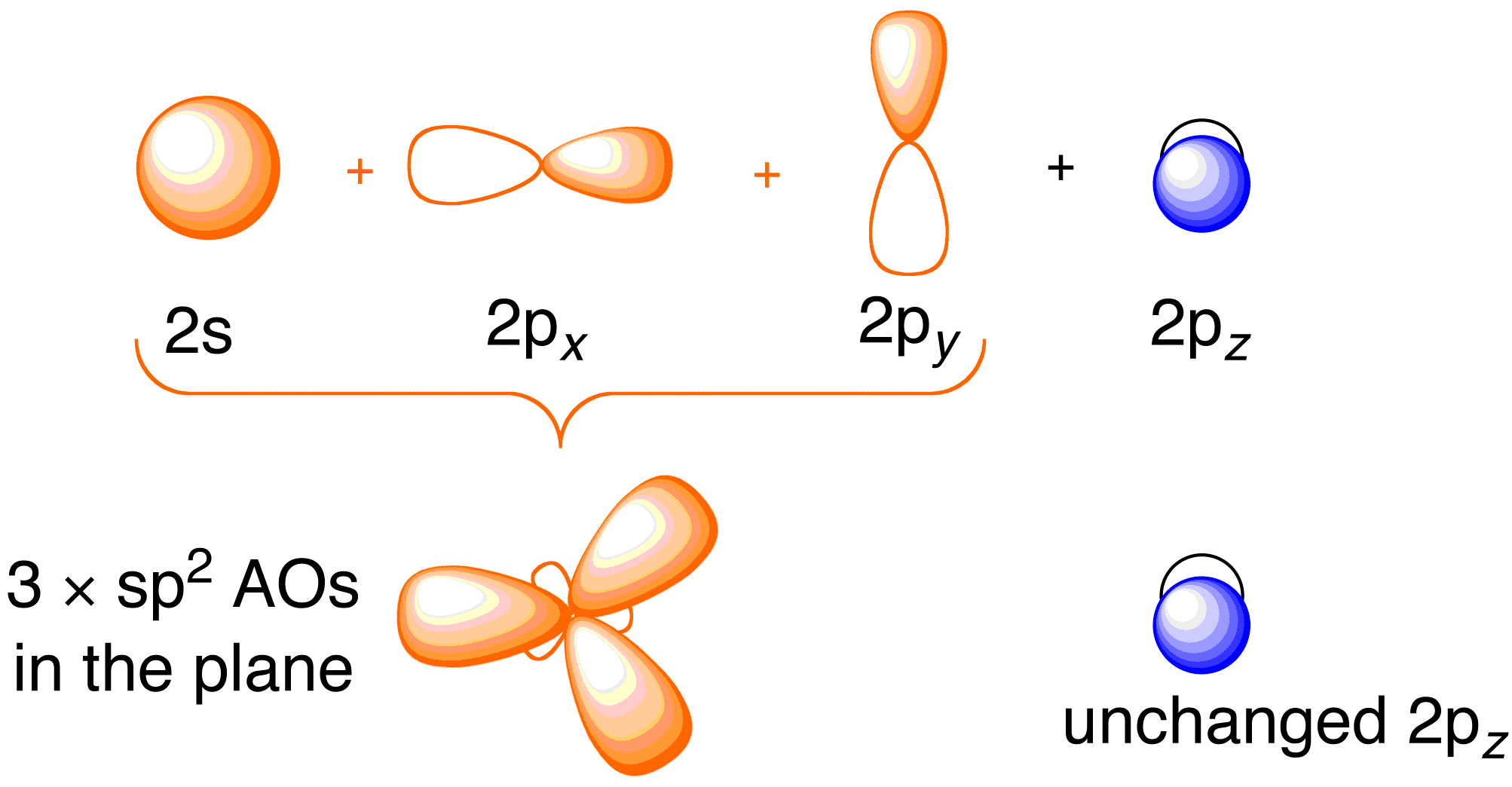
Figura 13.2. Hibridación de los orbitales atómicos del carbono para dar orbitales híbridos sp^2 para el enlace con átomos de hidrógeno en el eteno. Imagen utilizada con permiso de ChemTube (CC-SA-BY-NC; Nick Greeves).
El uso de orbitales híbridos en el enfoque de orbitales moleculares descrito aquí es meramente una conveniencia y no invoca la teoría del enlace de valencia (directamente). Se puede extraer una descripción idéntica utilizando exclusivamente orbitales atómicos en el carbono, pero la interpretación de las funciones de onda resultantes es menos intuitiva. Por ejemplo, el orbital molecular ith puede ser descrito a través de orbitales híbridos
o a través de orbitales atómicos.
donde {a_i\} y {c_i\} son coeficientes de la expansión. Cualquiera de las dos descripciones funcionará y ambas son aproximaciones idénticas, ya que
donde \{c_i\} son coeficientes que describen el orbital hibridado.
El enlace se produce a través de la mezcla de los electrones en los orbitales híbridos sp^2 del carbono y los electrones en los orbitales atómicos 1s de los cuatro átomos de hidrógeno (Figura 13.2. arriba a la izquierda) dando lugar al marco de enlace \sigma. El marco de enlace \pi resulta de los orbitales 2p_z no hibridados (Figura 13.2. arriba, derecha). La independencia de estos dos marcos se demuestra en el diagrama de orbitales moleculares resultante en la figura siguiente; la teoría de Hückel sólo se ocupa de describir los orbitales moleculares y las energías del marco de enlace \pi.

Figura 13.3: Orbitales moleculares que demuestran la separabilidad sigma-pi del marco de enlace \pi (azul) y los marcos de enlace \sigma (rojo) del etileno.
El tratamiento de Hückel sólo se ocupa de describir los orbitales moleculares y las energías del marco de enlace \pi.
Dado que la teoría de Hückel es una consideración especial de la teoría de orbitales moleculares, los orbitales moleculares | \psi_i |rangle pueden describirse como una combinación lineal de los orbitales atómicos 2p_z \phi en el carbono con sus correspondientes coeficientes \c_i}:
\
Para el análisis completo de la química cuántica utilizando la ecuación de Schrödinger (no se requiere para la clase de química orgánica), ver esta página de Libretexts.
Estos orbitales moleculares forman el marco de enlace π y como cada carbono contribuye con un electrón a este marco, sólo el orbital molecular más bajo ( | \psi_1 \rangle ) está ocupado (Figura ) en el estado básico. La configuración electrónica correspondiente es entonces \pi_1^2 .

Figura 13.4: Representación esquemática del marco de orbitales moleculares \pi para el etileno . Obsérvese que el orbital molecular antienlace tiene un nodo más que el orbital molecular de enlace, como era de esperar, ya que su energía es mayor.
HOMO y LUMO son acrónimos de orbital molecular de mayor ocupación y orbital molecular de menor desocupación, respectivamente, y suelen denominarse orbitales de frontera. La diferencia de energía entre el HOMO y el LUMO se denomina brecha HOMO-LUMO.
Los orbitales moleculares \pi calculados en 3D se muestran en la Figura 13.5.

Figura 13.5: Orbitales moleculares \pi calculados para el etileno . (izquierda) el orbital de enlace (ψ1) y (derecha) el orbital antienlace (ψ2).
Contribuidores
- Seymour Blinder (Profesor Emérito de Química y Física en la Universidad de Michigan, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
