Înțelegerea distribuțiilor normale

Într-o distribuție normală, datele sunt distribuite simetric, fără distorsiuni. Atunci când sunt reprezentate pe un grafic, datele urmează o formă de clopot, cu cele mai multe valori grupate în jurul unei regiuni centrale și care se micșorează pe măsură ce se îndepărtează de centru.

Distribuțiile normale se mai numesc și distribuții gaussiene sau curbe de clopot din cauza formei lor.

De ce contează distribuțiile normale?

Toate tipurile de variabile din științele naturale și sociale sunt distribuite normal sau aproximativ normal. Înălțimea, greutatea la naștere, capacitatea de citire, satisfacția la locul de muncă sau scorurile SAT sunt doar câteva exemple de astfel de variabile.

Pentru că variabilele distribuite normal sunt atât de comune, multe teste statistice sunt concepute pentru populații distribuite normal.

Înțelegerea proprietăților distribuțiilor normale înseamnă că puteți folosi statistica inferențială pentru a compara grupuri diferite și pentru a face estimări despre populații folosind eșantioane.

Care sunt proprietățile distribuțiilor normale?

Distribuțiile normale au caracteristici cheie care sunt ușor de observat în grafice:

• Media, mediana și modul sunt exact aceleași.
• Distribuția este simetrică în jurul mediei – jumătate din valori se situează sub medie și jumătate deasupra mediei.
• Distribuția poate fi descrisă prin două valori: media și abaterea standard.

Media este parametrul de localizare, în timp ce abaterea standard este parametrul de scară.

Media determină unde este centrat vârful curbei. Creșterea mediei deplasează curba spre dreapta, în timp ce scăderea acesteia deplasează curba spre stânga.

Ecartul standard întinde sau comprimă curba. O abatere standard mică are ca rezultat o curbă îngustă, în timp ce o abatere standard mare duce la o curbă lată.

Regula empirică

Regula empirică, sau regula 68-95-99.7, vă spune unde se află cele mai multe dintre valori într-o distribuție normală:

• În jur de 68% din valori se situează în limita a 1 abatere standard de la medie.
• În jur de 95% din valori se situează în limita a 2 abateri standard de la medie.
• În jur de 99,7% din valori se situează în limita a 3 abateri standard de la medie.

Colectați scorurile SAT de la studenții care participă la un nou curs de pregătire pentru test. Datele urmează o distribuție normală cu un scor mediu (M) de 1150 și o abatere standard (SD) de 150.

Să urmăm regula empirică:

• În jur de 68% din scoruri sunt cuprinse între 1000 și 1300, cu 1 abatere standard peste și sub medie.
• Aproximativ 95% din scoruri sunt cuprinse între 850 și 1450, cu 2 abateri standard deasupra și sub medie.
• Aproximativ 99,7% din scoruri sunt cuprinse între 700 și 1600, cu 3 abateri standard deasupra și sub medie.

Regula empirică este o modalitate rapidă de a obține o imagine de ansamblu a datelor dvs. și de a verifica dacă există valori aberante sau extreme care nu urmează acest model.

Dacă datele din eșantioane mici nu urmează îndeaproape acest model, atunci alte distribuții, cum ar fi distribuția t, pot fi mai potrivite. Odată ce ați identificat distribuția variabilei dumneavoastră, puteți aplica teste statistice adecvate.

Teorema limitei centrale

Teorema limitei centrale este baza pentru modul în care funcționează distribuțiile normale în statistică.

În cercetare, pentru a avea o idee bună despre media unei populații, ideal ar fi să colectați date din mai multe eșantioane aleatorii din cadrul populației. O distribuție de eșantionare a mediei este distribuția mediilor din aceste eșantioane diferite.

Teorema limitei centrale arată următoarele:

• Legea numerelor mari: Pe măsură ce crește dimensiunea eșantionului (sau numărul de eșantioane), atunci media eșantionului se va apropia de media populației.
• Cu mai multe eșantioane mari, distribuția de eșantionare a mediei este distribuită normal, chiar dacă variabila inițială nu este distribuită normal.

Testele statistice parametrice presupun de obicei că eșantioanele provin din populații distribuite normal, dar teorema limitei centrale înseamnă că această ipoteză nu este necesar să fie îndeplinită atunci când aveți un eșantion suficient de mare.

Puteți utiliza teste parametrice pentru eșantioane mari din populații cu orice tip de distribuție, atâta timp cât sunt îndeplinite alte ipoteze importante. O dimensiune a eșantionului de 30 sau mai mare este în general considerată mare.

Pentru eșantioane mici, ipoteza normalității este importantă deoarece distribuția de eșantionare a mediei nu este cunoscută. Pentru rezultate precise, trebuie să fiți sigur că populația este distribuită normal înainte de a putea utiliza teste parametrice cu eșantioane mici.

Formula curbei normale

După ce aveți media și abaterea standard a unei distribuții normale, puteți ajusta o curbă normală la datele dumneavoastră folosind o funcție de densitate de probabilitate.

Într-o funcție de densitate de probabilitate, aria de sub curbă vă indică probabilitatea. Distribuția normală este o distribuție de probabilitate, astfel încât aria totală de sub curbă este întotdeauna 1 sau 100%.

Formula funcției normale de densitate de probabilitate pare destul de complicată. Dar pentru a o folosi, trebuie doar să cunoașteți media și abaterea standard a populației.

Pentru orice valoare a lui x, puteți introduce media și abaterea standard în formulă pentru a afla densitatea de probabilitate a variabilei care ia acea valoare a lui x.

Formula densității de probabilitate normală	Explicație
	. f(x) = probabilitatea x = valoarea variabilei μ = media σ = abaterea standard σ2 = varianța

Vreți să cunoașteți probabilitatea ca scorurile SAT din eșantionul dumneavoastră să depășească 1380.

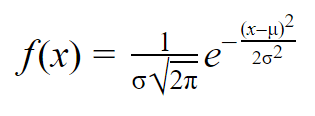Pe graficul funcției de densitate de probabilitate, probabilitatea este zona umbrită de sub curba care se află la dreapta locului unde scorurile SAT sunt egale cu 1380.

Puteți găsi valoarea probabilității acestui scor folosind distribuția normală standard.

Ce este distribuția normală standard?

Distribuția normală standard, numită și distribuția z, este o distribuție normală specială în care media este 0 și abaterea standard este 1.

Care distribuție normală este o versiune a distribuției normale standard care a fost întinsă sau comprimată și deplasată orizontal spre dreapta sau spre stânga.

În timp ce observațiile individuale din distribuțiile normale sunt denumite x, ele sunt denumite z în distribuția z. Fiecare distribuție normală poate fi convertită în distribuția normală standard prin transformarea valorilor individuale în scoruri z.

Scorurile z vă spun la câte abateri standard de la medie se află fiecare valoare.

Este suficient să cunoașteți media și abaterea standard a distribuției pentru a afla scorul z al unei valori.

Formula scorului Z	Explicație
	x = valoarea individuală μ = media σ = abaterea standard

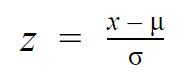Constituim distribuțiile normale în distribuția normală standard din mai multe motive:

• Pentru a afla probabilitatea ca observațiile dintr-o distribuție să se situeze deasupra sau sub o anumită valoare.
• Pentru a găsi probabilitatea ca media unui eșantion să difere semnificativ de o medie cunoscută a populației.
• Pentru a compara scorurile pe diferite distribuții cu medii și abateri standard diferite.

Căutarea probabilității folosind distribuția z

Care scor z este asociat cu o probabilitate, sau valoare p, care vă spune probabilitatea de apariție a valorilor sub acel scor z. Dacă transformați o valoare individuală într-un scor z, puteți găsi apoi probabilitatea de apariție a tuturor valorilor până la acea valoare într-o distribuție normală.

Pentru a găsi probabilitatea ca scorurile SAT din eșantionul dvs. să depășească 1380, găsiți mai întâi scorul z.

Media distribuției noastre este 1150, iar abaterea standard este 150. Scorul z vă spune la câte abateri standard se află 1380 față de medie.

Formula	Calculație
z = (x – μ) / σ	z = (1380 – 1150) / 150 z = 1.53

Pentru un scor z de 1,53, valoarea p este de 0,937. Aceasta este probabilitatea ca scorurile SAT să fie de 1380 sau mai puțin (93,7%) și este aria de sub curbă din stânga zonei umbrite.

Pentru a găsi zona umbrită, se îndepărtează 0.937 din 1, care este aria totală sub curbă.

Probabilitatea lui x>1380 = 1 – 0,937 = 0,063

Aceasta înseamnă că este probabil ca doar 6,3% din notele SAT din eșantionul dumneavoastră să depășească 1380.

Întrebări frecvente despre distribuțiile normale

.