Descriere simplă
Să considerăm mai întâi legătura pi din etenă din punctul de vedere al teoriei MO simplificate (în acest exemplu nu vom lua în considerare legăturile sigma din moleculă și ne vom gândi doar la legătura π). Începem cu doi orbitali atomici: un orbital 2p nehibridat de la fiecare carbon. Fiecare conține un singur electron. În teoria MO, cei doi orbitali atomici se combină matematic pentru a forma doi orbitali moleculari pi, un orbital de legătură pi de energie joasă și un orbital de antilegătură pi* de energie înaltă.

Orbitali moleculari pentru etenă (etilenă)
În orbitalul pi de legătură, cei doi lobi umbriți ai orbitalilor p interacționează constructiv unul cu celălalt, la fel ca și cei doi lobi neumbriți (rețineți, alegerea arbitrară a umbririi reprezintă semnele matematice (+) și (-) pentru funcția de undă matematică ce descrie orbitalul). Există o densitate crescută de electroni între cele două nuclee de carbon în orbitalul molecular – este o interacțiune de legătură.
În orbitalul pi* anti-legătură de energie mai mare, lobul umbrit al unui orbital p interacționează distructiv cu lobul neumbrit al celui de-al doilea orbital p, ceea ce duce la un nod între cele două nuclee și la o repulsie generală între nucleele de carbon.
Utilizând din nou principiul „construirii”, plasăm cei doi electroni în orbitalul molecular pi cu energie mai mică, de legătură. Orbitalul pi* anti-legătură rămâne gol.
Descriere MO mai detaliată a etenei
Teoria orbitalilor moleculari a fost aplicată cu mult succes la sistemele conjugate mari, în special la cele care conțin lanțuri de atomi de carbon cu legături simple și duble alternante. O aproximație introdusă de Hückel în 1931 ia în considerare doar electronii p delocalizați care se mișcă într-un cadru de legături \pi. Aceasta este, de fapt, o versiune mai sofisticată a unui model cu electroni liberi. Pentru un curs introductiv de chimie organică nu este necesar să folosim toate calculele matematice ale lui Hückel, dar pentru cei cărora le place să cerceteze mai în profunzime, este prezentată aici o analiză mai detaliată.
Cea mai simplă hidrocarbură de luat în considerare care prezintă legături \pi este etena (etilena), care este alcătuită din patru atomi de hidrogen și doi atomi de carbon. Experimental, știm că unghiurile H-C-H și H-C-C-C din etenă sunt de aproximativ 120°. Acest unghi sugerează că atomii de carbon sunt hibridizați sp2, ceea ce înseamnă că un orbital sp2 ocupat singular pe un carbon se suprapune cu un orbital s ocupat singular pe fiecare H și cu un lob sp2 ocupat singular pe celălalt C. Astfel, fiecare carbon formează un set de trei legături \sigma: două C-H (sp2 + s) și un C-C (sp2 + sp2) (partea (a) din figura 13.1. de mai jos).

Figura 13.1. (a) Cadrul cu legături σ este format prin suprapunerea a două seturi de orbitali hibrizi sp2 ai carbonului cu ocupare unică și a patru orbitali 1s ai hidrogenului cu ocupare unică pentru a forma legături pereche de electroni. Acest lucru utilizează 10 din cei 12 electroni de valență pentru a forma un total de cinci legături σ (patru legături C-H și o legătură C-C). (b) Pe fiecare atom de carbon rămâne un orbital 2pz nehibridat și ocupat singular pentru a forma o legătură π carbon-carbon. (Notă: prin convenție, în moleculele plane, axa perpendiculară pe planul molecular este axa z.)
Aproximația Hückel este utilizată pentru a determina energiile și formele orbitalilor moleculari \pi în sistemele conjugate. În cadrul aproximației Hückel, legăturile covalente din aceste hidrocarburi pot fi separate în două „cadre” independente: cadrul de legătură \sigma și cadrul de legătură \sigma. Funcțiile de undă utilizate pentru a descrie orbitalii de legătură în fiecare cadru rezultă din diferite combinații de orbitali atomici. Metoda se limitează la abordarea hidrocarburilor conjugate și, în mod specific, sunt incluși doar orbitalii moleculari cu electroni \pi, deoarece aceștia determină proprietățile generale ale acestor molecule; electronii sigma sunt ignorați. Acest lucru se numește separabilitate sigma-pi și este justificat de ortogonalitatea orbitalilor \sigma și \pi în moleculele plane. Din acest motiv, metoda Hückel este limitată la sistemele plane. Aproximarea Hückel presupune că electronii din legăturile \spi „simt” un potențial electrostatic datorat întregului cadru de legături \sigma din moleculă (adică se concentrează doar pe formarea legăturilor \spi, având în vedere că cadrul de legături \sigma a fost deja format).
Sisteme conjugate
Un sistem conjugat are o regiune de orbitali p suprapuși, care acoperă legăturile simple interjacente, care permit o delocalizare a electronilor \pi în toți orbitalii p adiacenți aliniați. Acești electroni \pi nu aparțin unei singure legături sau unui singur atom, ci mai degrabă unui grup de atomi.
Etenă
Înainte de a lua în considerare tratamentul Hückel pentru etenă, este benefic să trecem în revistă imaginea generală a legăturilor din moleculă. Legătura în etenă implică hibridizarea sp^2 a orbitalilor atomici 2s , 2p_x și 2p_y de pe fiecare atom de carbon; lăsând neatinși orbitalii 2p_z (figura 13.2).
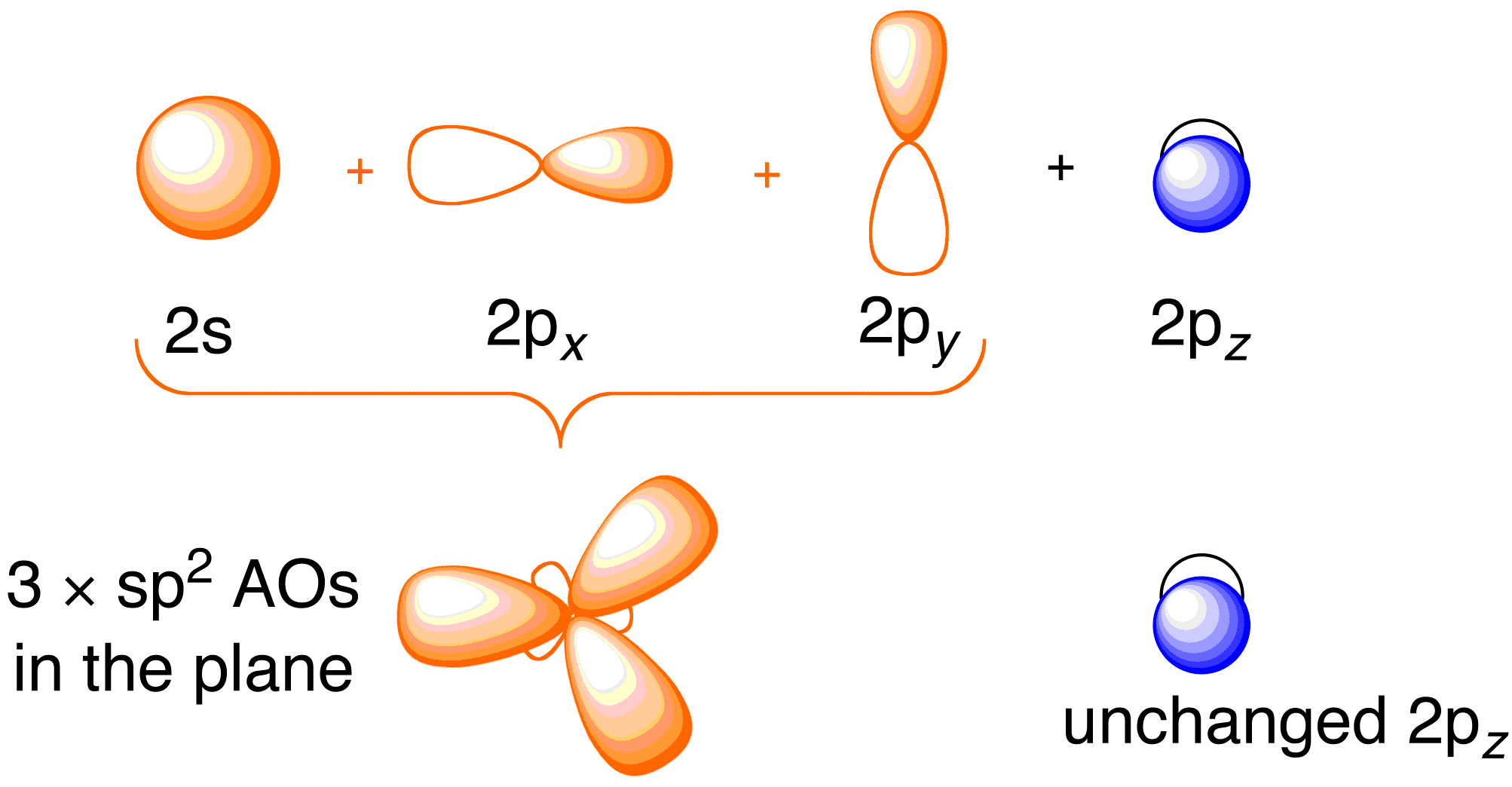
Figura 13.2. Hibridizarea orbitalilor atomici ai carbonului pentru a obține orbitali hibrizi sp^2 pentru legarea de atomii de hidrogen în etenă. Imagine utilizată cu permisiunea ChemTube (CC-SA-BY-NC; Nick Greeves).
Utilizarea orbitalilor hibrizi în abordarea orbitalilor moleculari descrisă aici este doar o comoditate și nu invocă teoria legăturii de valență (în mod direct). O descriere identică poate fi extrasă folosind exclusiv orbitali atomici pe carbon, dar interpretarea funcțiilor de undă rezultate este mai puțin intuitivă. De exemplu, al i-lea orbital molecular poate fi descris prin intermediul orbitalilor hibrizi
\
sau prin intermediul orbitalilor atomici.
\
unde \{a_i\} și \{c_i\} sunt coeficienți ai expansiunii. Oricare dintre descrieri va funcționa și ambele sunt abordări identice deoarece
\
unde \{c_i\} sunt coeficienți care descriu orbitalul hibridizat.
Legătura are loc prin amestecul electronilor din orbitalii hibrizi sp^2 de pe carbon și electronii din orbitalii atomici 1s ai celor patru atomi de hidrogen (figura 13.2. sus, în stânga), rezultând cadrul de legătură \sigma. Cadrul de legături \pi – rezultă din orbitalii 2p_z nehibridizați (figura 13.2. de mai sus, dreapta). Independența acestor două cadre este demonstrată în diagrama orbitalilor moleculari rezultată în figura de mai jos; teoria Hückel este preocupată doar de descrierea orbitalilor moleculari și a energiilor cadrului de legătură \pi.

Figura 13.3: Orbitalii moleculari care demonstrează separabilitatea sigma-pi a cadrului de legătură \pi (albastru) și a cadrului de legătură \sigma (roșu) al etilenei.
Tratarea lui Hückel este preocupată doar de descrierea orbitalilor moleculari și a energiilor cadrului de legătură \pi.
Din moment ce teoria Hückel este o considerație specială a teoriei orbitalilor moleculari, orbitalii moleculari | \psi_i \rangul \ pot fi descriși ca o combinație liniară a orbitalilor atomici 2p_z \phi la carbon cu coeficienții lor corespunzători \{c_i\}:
\
Pentru analiza completă a chimiei cuantice folosind ecuația lui Schrödinger (nu este necesară pentru cursul de chimie organică), consultați această pagină Libretexts.
Acești orbitali moleculari formează cadrul de legătură π și, deoarece fiecare carbon contribuie cu câte un electron la acest cadru, doar cel mai mic orbital molecular ( | \psi_1 \rangle ) este ocupat (Figura ) în starea fundamentală. Configurația electronică corespunzătoare este atunci \pi_1^2 .

Figura 13.4: Reprezentarea schematică a cadrului orbitalilor moleculari \pi pentru etilenă . Observați că orbitalul molecular de antilegătură are cu un nod mai mult decât orbitalul molecular de legătură, așa cum era de așteptat, deoarece are o energie mai mare.
HOMO și LUMO sunt acronimele pentru orbitalul molecular cel mai înalt ocupat și, respectiv, cel mai mic orbital molecular neocupat și sunt adesea denumite orbitali de frontieră. Diferența de energie dintre HOMO și LUMO se numește decalajul HOMO-LUMO.
Orbitalii moleculari \pi calculați 3-D sunt prezentați în figura 13.5.

Figura 13.5: Orbitalii moleculari \pi calculați pentru etilenă . (stânga) orbitalul de legătură (ψ1) și (dreapta) orbitalul de antilegătură (ψ2).
Contribuitori
- Seymour Blinder (profesor emerit de chimie și fizică la Universitatea din Michigan, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
.
