Un triunghi cu un unghi drept se numește triunghi dreptunghic. Latura opusă unghiului dreptunghic se numește ipotenuza triunghiului. Celelalte două laturi se numesc picioare. Celelalte două unghiuri nu au un nume special, dar ele sunt întotdeauna complementare. Înțelegi de ce? Suma totală a unghiurilor unui triunghi este de 180 de grade, iar unghiul dreptunghic este de 90 de grade, deci celelalte două trebuie să însumeze 90 de grade.
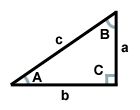
Triunghiul de mai sus are ca ipotenuză latura c, ca laturi a și b picioarele și ca unghi C unghiul dreptunghic. Unghiurile A și B sunt complementare.
Există două tipuri de triunghiuri drepte pe care orice matematician ar trebui să le cunoască foarte bine. Unul este triunghiul dreptunghic format atunci când se trasează o altitudine de la un vârf al unui triunghi echilateral, formând două triunghiuri dreptunghice congruente. Unghiurile triunghiului vor fi de 30, 60 și 90 de grade, ceea ce dă triunghiului numele său: triunghiul 30-60-90. Raportul lungimilor laturilor în astfel de triunghiuri este întotdeauna același: dacă piciorul opus unghiului de 30 de grade are lungimea x, piciorul opus unghiului de 60 de grade va avea lungimea x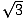
, iar ipotenuza de vizavi de unghiul drept va fi 2x. Iată un triunghi 30-60-90 ilustrat mai jos.
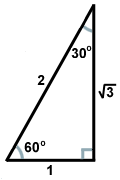
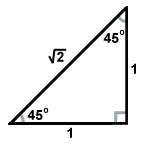
Celălalt triunghi dreptunghic obișnuit rezultă din perechea de triunghiuri creată atunci când o diagonală împarte un pătrat în două triunghiuri. Fiecare dintre aceste triunghiuri este congruent și are unghiuri de măsuri 45, 45 și 90 de grade. Dacă picioarele opuse unghiurilor de 45 de grade au lungimea x, ipotenuza are o lungime de x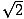
. Acest raport este valabil pentru toate triunghiurile 45-45-90. Triunghiurile 45-45-90 sunt adesea numite și triunghiuri dreptunghice isoscele.
O ultimă caracteristică de reținut este aceea că catetele unui triunghi dreptunghic sunt și altitudini ale triunghiului. Prin urmare, aria unui triunghi dreptunghic este jumătate din produsul lungimilor picioarelor sale.