I en normalfördelning är data symmetriskt fördelade utan skevhet. När data ritas upp i en graf följer data en klockform, där de flesta värden samlas runt ett centralt område och avtar när de kommer längre bort från centrum.
Normalfördelningar kallas också för Gaussfördelningar eller klockkurvor på grund av deras form.

Varför är normalfördelningar viktiga?
Alla typer av variabler inom natur- och samhällsvetenskaperna är normal- eller ungefär normalt fördelade. Längd, födelsevikt, läsförmåga, arbetstillfredsställelse eller SAT-poäng är bara några exempel på sådana variabler.
Då normalfördelade variabler är så vanliga är många statistiska tester utformade för normalfördelade populationer.
Om du förstår normalfördelningarnas egenskaper kan du använda inferensstatistik för att jämföra olika grupper och göra uppskattningar om populationer med hjälp av stickprov.
Vilka egenskaper har normalfördelningar?
Normalfördelningar har viktiga egenskaper som är lätta att upptäcka i grafer:
- Medelvärdet, medianen och läget är exakt desamma.
- Fördelningen är symmetrisk kring medelvärdet – hälften av värdena faller under medelvärdet och hälften över medelvärdet.
- Fördelningen kan beskrivas med två värden: medelvärdet och standardavvikelsen.


Medelvärdet är lägesparametern medan standardavvikelsen är skalparametern.
Medelvärdet avgör var kurvans topp är centrerad. En ökning av medelvärdet flyttar kurvan till höger, medan en minskning flyttar kurvan till vänster.


Standardavvikelsen sträcker eller klämmer kurvan. En liten standardavvikelse resulterar i en smal kurva, medan en stor standardavvikelse leder till en bred kurva.


Empirisk regel
Den empiriska regeln, eller 68-95-99.7-regeln, talar om var de flesta av dina värden ligger i en normalfördelning:
- Omkring 68 % av värdena ligger inom 1 standardavvikelse från medelvärdet.
- Omkring 95 % av värdena ligger inom 2 standardavvikelser från medelvärdet.
- Omkring 99,7 % av värdena ligger inom 3 standardavvikelser från medelvärdet.
Med hjälp av den empiriska regeln:
- Omkring 68 % av poängen ligger mellan 1000 och 1300, 1 standardavvikelse över och under medelvärdet.
- Omkring 95 % av poängen ligger mellan 850 och 1450, 2 standardavvikelser över och under medelvärdet.
- Omkring 99,7 % av poängen ligger mellan 700 och 1600, 3 standardavvikelser över och under medelvärdet.


Den empiriska regeln är ett snabbt sätt att få en överblick över dina data och kontrollera om det finns några outliers eller extrema värden som inte följer det här mönstret.
Om data från små stickprov inte följer det här mönstret i hög grad kan andra fördelningar som t-fördelningen vara mer lämpliga. När du har identifierat fördelningen av din variabel kan du tillämpa lämpliga statistiska tester.
Centrala gränssatsen
Den centrala gränssatsen ligger till grund för hur normalfördelningar fungerar i statistiken.
I forskning, för att få en god uppfattning om en populations medelvärde, samlar du helst in data från flera slumpmässiga urval inom populationen. En samplingsfördelning av medelvärdet är fördelningen av medelvärdena för dessa olika stickprov.
Den centrala gränssatsen visar följande:
- Law of Large Numbers: När du ökar provstorleken (eller antalet prov) kommer provets medelvärde att närma sig populationens medelvärde.
- Med flera stora prov är provfördelningen av medelvärdet normalfördelad, även om din ursprungliga variabel inte är normalfördelad.
Parametriska statistiska test utgår vanligtvis från att proverna kommer från normalfördelade populationer, men den centrala gränssatsen innebär att detta antagande inte behöver uppfyllas när du har ett tillräckligt stort prov.
Du kan använda parametriska test för stora prover från populationer med vilken typ av fördelning som helst så länge som andra viktiga antaganden uppfylls. Ett urval på 30 eller mer anses i allmänhet vara stort.
För små urval är antagandet om normalitet viktigt eftersom urvalsfördelningen för medelvärdet inte är känd. För exakta resultat måste du vara säker på att populationen är normalfördelad innan du kan använda parametriska test med små urval.
Formel för normalkurvan
När du har medelvärdet och standardavvikelsen för en normalfördelning kan du anpassa en normalkurva till dina data med hjälp av en sannolikhetstäthetsfunktion.


I en sannolikhetstäthetsfunktion säger arean under kurvan något om sannolikheten. Normalfördelningen är en sannolikhetsfördelning, så den totala arean under kurvan är alltid 1 eller 100 %.
Formeln för den normala sannolikhetstäthetsfunktionen ser ganska komplicerad ut. Men för att använda den behöver du bara känna till populationens medelvärde och standardavvikelse.
För varje värde på x kan du sätta in medelvärdet och standardavvikelsen i formeln för att hitta sannolikhetstätheten för variabeln som antar detta värde på x.
| Normal sannolikhetstäthetsformel | förklaring |
|---|---|
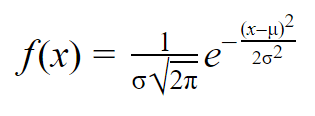 |
|
På grafen för sannolikhetstäthetsfunktionen är sannolikheten det skuggade området under kurvan som ligger till höger om det område där dina SAT-poäng är lika med 1380.


Du kan hitta sannolikhetsvärdet för detta poängvärde med hjälp av standardnormalfördelningen.
Vad är standardnormalfördelningen?
Standardnormalfördelningen, även kallad z-fördelningen, är en speciell normalfördelning där medelvärdet är 0 och standardavvikelsen är 1.
Alla normalfördelningar är en version av standardnormalfördelningen som har sträckts eller pressats och flyttats horisontellt till höger eller vänster.


Men medan enskilda observationer från normalfördelningar benämns x, benämns de z i z-fördelningen. Varje normalfördelning kan omvandlas till standardnormalfördelningen genom att omvandla de enskilda värdena till z-värden.
Z-värden talar om hur många standardavvikelser från medelvärdet som varje värde ligger.


Du behöver bara känna till medelvärdet och standardavvikelsen för din fördelning för att hitta z-poängen för ett värde.
| Z-score Formel | Förklaring |
|---|---|
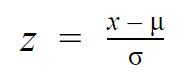 |
|
Vi omvandlar normalfördelningar till standardnormalfördelningen av flera skäl:
- För att hitta sannolikheten för att observationerna i en fördelning ligger över eller under ett givet värde.
- För att hitta sannolikheten för att ett urvalsmedelvärde skiljer sig signifikant från ett känt populationsmedelvärde.
- För att jämföra resultat på olika fördelningar med olika medelvärden och standardavvikelser.
Finnande av sannolikhet med hjälp av z-fördelningen
Varje z-värde är förknippat med en sannolikhet, eller ett p-värde, som talar om hur stor sannolikhet det är för att värden som ligger under det z-värdet inträffar. Om du omvandlar ett enskilt värde till ett z-värde kan du sedan hitta sannolikheten för att alla värden upp till det värdet förekommer i en normalfördelning.
Medelvärdet i vår fördelning är 1150 och standardavvikelsen är 150. Z-värdet anger hur många standardavvikelser 1380 ligger från medelvärdet.
| Formel | Beräkning |
|---|---|
| z = (x – μ) / σ | z = (1380 – 1150) / 150 z = 1.53 |
För ett z-värde på 1,53 är p-värdet 0,937. Detta är sannolikheten för att SAT-poängen är 1380 eller mindre (93,7 %), och det är arean under kurvan till vänster om det skuggade området.


För att hitta det skuggade området tar man bort 0.937 från 1, vilket är den totala ytan under kurvan.
Sannolikheten för x>1380 = 1 – 0,937 = 0,063
Det innebär att det är troligt att endast 6,3 % av SAT-poängen i ditt urval överstiger 1380.
Högre vanliga frågor om normalfördelningar
I en normalfördelning är data symmetriskt fördelade utan skevhet. De flesta värden samlas kring ett centralt område och värdena avtar när de kommer längre bort från centrum.
Måtten för central tendens (medelvärde, läge och median) är exakt desamma i en normalfördelning.
Standardnormalfördelningen, även kallad z-fördelningen, är en speciell normalfördelning där medelvärdet är 0 och standardavvikelsen 1.
Alla normalfördelningar kan omvandlas till standardnormalfördelningen genom att omvandla de enskilda värdena till z-värden. I en z-fördelning säger z-poängen hur många standardavvikelser från medelvärdet varje värde ligger.
Den empiriska regeln, eller 68-95-99,7-regeln, talar om var de flesta värdena ligger i en normalfördelning:
- Omkring 68 % av värdena ligger inom 1 standardavvikelse från medelvärdet.
- Omkring 95 % av värdena ligger inom 2 standardavvikelser från medelvärdet.
- Omkring 99,7 % av värdena ligger inom 3 standardavvikelser från medelvärdet.
Den empiriska regeln är ett snabbt sätt att få en överblick över dina data och kontrollera om det finns några outliers eller extremvärden som inte följer detta mönster.
T-fördelningen är ett sätt att beskriva en uppsättning observationer där de flesta observationerna faller nära medelvärdet och resten av observationerna utgör svansarna på vardera sidan. Det är en typ av normalfördelning som används för mindre urvalsstorlekar, där variansen i data är okänd.
T-fördelningen bildar en klockkurva när den plottas på en graf. Den kan beskrivas matematiskt med hjälp av medelvärdet och standardavvikelsen.

