Logistisk regressionsanalys

Utfallet i logistisk regressionsanalys kodas ofta som 0 eller 1, där 1 indikerar att utfallet av intresse är närvarande och 0 indikerar att utfallet av intresse är frånvarande. Om vi definierar p som sannolikheten för att utfallet är 1 kan den multipla logistiska regressionsmodellen skrivas på följande sätt:

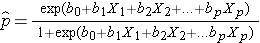
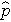är den förväntade sannolikheten för att utfallet är närvarande; X1 till Xp är skilda oberoende variabler; och b0 till bp är regressionskoefficienterna. Den multipla logistiska regressionsmodellen skrivs ibland på annat sätt. I följande form är utfallet den förväntade logaritmen av oddsen för att utfallet är närvarande,

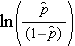
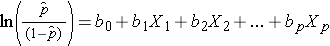
Bemärk att den högra sidan av ekvationen ovan ser ut som den multipla linjära regressionsekvationen. Tekniken för att skatta regressionskoefficienterna i en logistisk regressionsmodell skiljer sig dock från den som används för att skatta regressionskoefficienterna i en multipel linjär regressionsmodell. I logistisk regression anger de koefficienter som härleds från modellen (t.ex. b1) förändringen i de förväntade logaritmiska oddsen i förhållande till en enhetsförändring i X1, med alla andra prediktorer konstanta. Därför ger antilogan av en uppskattad regressionskoefficient, exp(bi), ett oddskvotstal, vilket illustreras i exemplet nedan.

Exempel på logistisk regression – Samband mellan fetma och CVD

Vi har tidigare analyserat data från en studie som är utformad för att bedöma sambandet mellan fetma (definierat som BMI > 30) och inträffad kardiovaskulär sjukdom. Data samlades in från deltagare som var mellan 35 och 65 år gamla och fria från kardiovaskulär sjukdom (CVD) vid baslinjen. Varje deltagare följdes i 10 år för utveckling av kardiovaskulär sjukdom. En sammanfattning av uppgifterna finns på sidan 2 i denna modul. Den ojusterade eller grova relativa risken var RR = 1,78 och den ojusterade eller grova oddskvoten var OR = 1,93. Vi fastställde också att ålder var en confounder, och med hjälp av Cochran-Mantel-Haenszel-metoden uppskattade vi en justerad relativ risk på RRCMH =1,44 och en justerad oddskvot på ORCMH =1,52. Vi kommer nu att använda logistisk regressionsanalys för att bedöma sambandet mellan fetma och incident kardiovaskulär sjukdom med justering för ålder.

Den logistiska regressionsanalysen avslöjar följande:

Oberoende variabel	Regressionskoefficient	Chi-square	P-värde
Intercept	-2.367	307.38	0.0001
Fetma	0,658	9,87	0.0017

Den enkla logistiska regressionsmodellen relaterar fetma till log oddset för insjuknande i CVD:

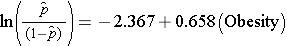
Fetma är en indikatorvariabel i modellen, kodad enligt följande: 1=obesitas och 0=inte obesitas. Log-oddset för incident CVD är 0,658 gånger högre hos personer som är överviktiga jämfört med personer som inte är överviktiga. Om vi tar antilog av regressionskoefficienten, exp(0,658) = 1,93, får vi den råa eller ojusterade oddskvoten. Oddsen för att drabbas av CVD är 1,93 gånger högre bland överviktiga personer jämfört med icke överviktiga personer. Sambandet mellan fetma och CVD är statistiskt signifikant (p=0,0017). Observera att teststatistiken för att bedöma betydelsen av regressionsparametrarna i logistisk regressionsanalys bygger på chi-square-statistik, i motsats till t-statistik som var fallet med linjär regressionsanalys. Detta beror på att en annan skattningsteknik, kallad maximum likelihood estimation, används för att skatta regressionsparametrarna (se Hosmer och Lemeshow3 för tekniska detaljer).

Många statistiska datapaket genererar också oddskvoter samt 95 % konfidensintervall för oddskvoterna som en del av deras logistiska regressionsanalysförfarande. I det här exemplet är uppskattningen av oddskvoten 1,93 och 95 % konfidensintervallet är (1,281, 2,913).

När vi undersökte sambandet mellan fetma och hjärt-kärlsjukdom har vi tidigare fastställt att åldern var en störande faktor.Följande multipla logistiska regressionsmodell uppskattar sambandet mellan fetma och inträffad hjärt-kärlsjukdom, med justering för ålder. I modellen tar vi återigen hänsyn till två åldersgrupper (mindre än 50 år och 50 år och äldre). I analysen kodas åldersgruppen på följande sätt: 1=50 år och äldre och 0=mindre än 50 år.

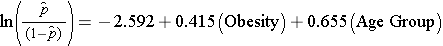
Om vi tar antilogan av regressionskoefficienten förknippad med fetma, exp(0,415) = 1,52 får vi oddskvoten justerad för ålder. Oddsen för att drabbas av CVD är 1,52 gånger högre bland överviktiga personer jämfört med icke överviktiga personer, justerat för ålder. I avsnitt 9.2 använde vi Cochran-Mantel-Haenszel-metoden för att generera en oddskvot justerad för ålder och fann följande:

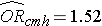
Detta illustrerar hur multipel logistisk regressionsanalys kan användas för att ta hänsyn till förväxlingsfaktorer. Modellerna kan utökas för att ta hänsyn till flera störande variabler samtidigt. Multipel logistisk regressionsanalys kan också användas för att bedöma confounding och effektmodifiering, och tillvägagångssätten är identiska med dem som används vid multipel linjär regressionsanalys. Multipel logistisk regressionsanalys kan också användas för att undersöka effekten av flera riskfaktorer (i motsats till att fokusera på en enda riskfaktor) på ett dikotomt utfall.

Exempel – Riskfaktorer som är förknippade med låg födelsevikt hos spädbarn

Förutsatt att utredarna också är intresserade av negativa utfall under graviditeten, inklusive graviditetsdiabetes, preeklampsi (dvs. graviditetsinducerad högt blodtryck) och för tidigt födelsearbete. Minns att studien omfattade 832 gravida kvinnor som lämnar demografiska och kliniska uppgifter. I studiens urval utvecklade 22 (2,7 %) kvinnor preeklampsi, 35 (4,2 %) graviditetsdiabetes och 40 (4,8 %) förtidsarbete. Antag att vi vill bedöma om det finns skillnader i vart och ett av dessa negativa graviditetsutfall beroende på ras/etnicitet, justerat för moderns ålder. Tre separata logistiska regressionsanalyser genomfördes för att relatera varje resultat separat till tre dummy- eller indikatorvariabler som återspeglar moderns ras och moderns ålder i år. Resultaten redovisas nedan.

Resultat: Preeklampsi	Regressionskoefficient	Chi-kvadrat	P-värde	Odds Ratio (95 % CI)
Intercept	-3.066	4.518	0.0335	–
Svart ras	2.191	12.640	0.0004	8.948 (2.673, 29.949)
Hispanisk ras	-0.1053	0.0325	0.8570	0.900 (0,286, 2,829)
Andra ras	0,0586	0,0021	0.9046	1.060 (0.104, 3.698)
Mödrars ålder (år)	-0.0252	0.3574	0,5500	0,975 (0,898, 1,059)

Den enda statistiskt signifikanta skillnaden i preeklampsi är mellan svarta och vita mödrar.

Svarta mödrar löper nästan 9 gånger större risk att utveckla preeklampsi än vita mödrar, justerat för moderns ålder. Det 95-procentiga konfidensintervallet för oddskvoten som jämför svarta respektive vita kvinnor som utvecklar preeklampsi är mycket brett (2,673 till 29,949). Detta beror på att det finns ett litet antal utfallshändelser (endast 22 kvinnor utvecklar preeklampsi i det totala urvalet) och ett litet antal kvinnor av svart ras i studien. Därför bör detta samband tolkas med försiktighet.

Och även om oddskvoten är statistiskt signifikant tyder konfidensintervallet på att storleken på effekten kan vara allt från en 2,6-faldig ökning till en 29,9-faldig ökning. En större studie behövs för att generera en mer exakt uppskattning av effekten.

Gestationsdiabetes	Regressionskoefficient	Chi-square	P-värde	Odds Ratio (95% CI)
Intercept	-5.823	22.968	0.0001	–
Svart ras	1.621	6.660	0,0099	5,056 (1,477, 17,312)
Hispanisk ras	0,581	1.766	0.1839	1.787 (0.759, 4.207)
Andra ras	1.348	5.917	0.0150	3.848 (1.299, 11.395)
Mammans ålder (år)	0.071	4.314	0,0378	1,073 (1,004, 1,147)

När det gäller graviditetsdiabetes finns det statistiskt signifikanta skillnader mellan svarta och vita mödrar (p=0,0099) och mellan mödrar som identifierar sig själva som annan ras jämfört med vita (p=0,0150), justerat för moderns ålder. Moderns ålder är också statistiskt signifikant (p=0,0378), där äldre kvinnor löper större risk att utveckla graviditetsdiabetes, justerat för ras/etnicitet.

Resultat: För tidig födsel	Regressionskoefficient	Chi-kvadrat	P-värde	Odds Ratio (95 % KI)
Intercept	-1.443	1.602	0.2056	–
Svart ras	-0,082	0,015	0.9039	0,921 (0,244, 3,483)
Hispanisk ras	-1,564	9.497	0,0021	0,209 (0,077, 0,566)
Andra ras	0.548	1.124	0.2890	1.730 (0.628,4.767)
Mammans ålder (år.)	00,037	1,198	0,2737	0,963 (0,901, 1,030)

Med avseende på förlossningsarbete före termin är den enda statistiskt signifikanta skillnaden mellan spansktalande och vita mammor (p=0,0021). Hispaniska mödrar har 80 % lägre sannolikhet att utveckla förtidsarbete än vita mödrar (oddskvot = 0,209), justerat för moderns ålder.

Multivariabla metoder är beräkningsmässigt komplexa och kräver i allmänhet användning av ett statistiskt beräkningspaket. Multivariabla metoder kan användas för att bedöma och justera för confounding, för att avgöra om det finns en effekt modifiering eller för att bedöma sambanden mellan flera exponerings- eller riskfaktorer på ett utfall samtidigt. Multivariabla analyser är komplexa och bör alltid planeras så att de återspeglar biologiskt rimliga samband. Även om det är relativt enkelt att beakta ytterligare en variabel i en multipel linjär eller multipel logistisk regressionsmodell, bör endast variabler som är kliniskt meningsfulla inkluderas.

Det är viktigt att komma ihåg att multivariabla modeller endast kan justera eller redogöra för skillnader i störande variabler som mättes i studien. Dessutom bör multivariabla modeller endast användas för att ta hänsyn till förväxlingsvariabler när det finns en viss överlappning i fördelningen av förväxlingsvariablerna respektive riskfaktorgrupper.

Stratifierade analyser är mycket informativa, men om proverna i specifika strata är för små kan analyserna sakna precision. Vid planeringen av studier måste utredarna vara noga uppmärksamma på potentiella effektmodifierare. Om det finns en misstanke om att ett samband mellan en exponering eller riskfaktor skiljer sig åt i specifika grupper, måste studien utformas så att man säkerställer ett tillräckligt antal deltagare i var och en av dessa grupper. Formler för urvalsstorlek måste användas för att fastställa det antal försökspersoner som krävs i varje stratum för att säkerställa tillräcklig precision eller styrka i analysen.

tillbaka till början | föregående sida | nästa sida