Enklare beskrivning
Låt oss först betrakta pi-bindningen i eten från en förenklad MO-teoretisk synvinkel (i det här exemplet kommer vi att bortse från sigma-bindningarna i molekylen och bara tänka på π-bindningen). Vi börjar med två atomorbitaler: en ohybridiserad 2p-orbital från varje kol. Var och en innehåller en enda elektron. I MO-teorin kombineras de två atomära matematiskt för att bilda två pi-molekylära orbitaler, en pi-bindningsorbital med låg energi och en pi*-antibindningsorbital med hög energi.

Molekylära orbitaler för eten (eten)
I den bindande pi-orbitalen interagerar de två skuggade lobbarna i p-orbitalerna konstruktivt med varandra, liksom de två oskuggade lobbarna (kom ihåg att det godtyckliga valet av skuggning representerar matematiska (+)- och (-)-tecken för den matematiska vågfunktion som beskriver orbitalet). Det finns en ökad elektrontäthet mellan de två kolkärnorna i molekylorbitalet – det är en bindningsinteraktion.
I den högre energirelaterade antibindande pi*-orbitalet interagerar den skuggade loben i den ena p-orbitalet destruktivt med den oskuggade loben i den andra p-orbitalet, vilket leder till en knut mellan de två atomkärnorna och en övergripande repulsion mellan kolkärnorna.
Också med hjälp av ”uppbyggnadsprincipen” placerar vi de två elektronerna i den lägre energirika, bindande pi-molekylorbitalen. Den antibindande pi*-orbitalen förblir tom.
En mer detaljerad MO-beskrivning av eten
Molekylorbitalteorin har med stor framgång tillämpats på stora konjugerade system, särskilt sådana som innehåller kedjor av kolatomer med omväxlande enkel- och dubbelbindningar. En approximation som introducerades av Hückel 1931 tar endast hänsyn till de delokaliserade p-elektronerna som rör sig i en ram av \pi -bindningar. Detta är i själva verket en mer sofistikerad version av en modell med fria elektroner. För en introduktionskurs i organisk kemi behöver vi inte använda hela Hückels matematik, men för dem som vill gräva djupare ges här en mer detaljerad analys.
Det enklaste kolväte att betrakta som uppvisar \pi-bindningar är ethen (eten), som består av fyra väteatomer och två kolatomer. Experimentellt vet vi att H-C-H- och H-C-C-C-vinkeln i eten är ungefär 120°. Denna vinkel tyder på att kolatomerna är sp2-hybridiserade, vilket innebär att en enkelt ockuperad sp2-orbital på ett kol överlappar med en enkelt ockuperad s-orbital på varje H och en enkelt ockuperad sp2-lob på det andra C. Således bildar varje kol en uppsättning av tre \sigma-bindningar: två C-H (sp2 + s) och en C-C (sp2 + sp2) (del (a) i figur 13.1. nedan).

Figur 13.1. (a) Det σ-bundna ramverket bildas genom överlappning av två uppsättningar singelockuperade kol sp2 hybridorbitaler och fyra singelockuperade väte 1sorbitaler för att bilda elektronparbindningar. Detta använder 10 av de 12 valenselektronerna för att bilda totalt fem σ-bindningar (fyra C-H-bindningar och en C-C-bindning). (b) En singelockuperad ohybridiserad 2pz-orbital återstår på varje kolatom för att bilda en kol-kol π-bindning. (Anmärkning: enligt konvention är i plana molekyler den axel som är vinkelrät mot molekylplanet z-axeln.)
Hückel-approximationen används för att bestämma energierna och formerna hos \pi-molekylorbitalerna i konjugerade system. Inom Hückel-approximationen kan den kovalenta bindningen i dessa kolväten delas upp i två oberoende ”ramar”: \sigma -bindningsramen och \sigma -bindningsramen. De vågfunktioner som används för att beskriva bindningsorbitalerna i varje ram är resultatet av olika kombinationer av atomorbitaler. Metoden begränsar sig till att behandla konjugerade kolväten och specifikt inkluderas endast \pi-elektronernas molekylära orbitaler eftersom dessa bestämmer de allmänna egenskaperna hos dessa molekyler; Sigma-elektronerna ignoreras. Detta kallas sigma-pi-separabilitet och motiveras av att \sigma- och \pi-orbitaler är ortogonala i plana molekyler. Av denna anledning är Hückelmetoden begränsad till plana system. Hückel-approximationen antar att elektronerna i \pi-bindningarna ”känner” en elektrostatisk potential på grund av hela \sigma-bindningsramen i molekylen (dvs. den fokuserar endast på bildandet av \pi-bindningar, med tanke på att \sigma-bindningsramen redan har bildats).
Konjugerade system
Ett konjugerat system har ett område med överlappande p-orbitaler, som överbryggar de intilliggande singelbindningarna, vilket möjliggör en delokalisering av \pi-elektroner över alla intilliggande, justerade p-orbitaler. Dessa \pi-elektroner tillhör inte en enskild bindning eller atom, utan snarare en grupp av atomer.
Ethen
För att överväga Hückel-behandlingen för eten är det fördelaktigt att se över den allmänna bindningsbilden för molekylen. Bindning i eten innebär sp^2-hybridisering av 2s , 2p_x och 2p_y-atomorbitalerna på varje kolatom; 2p_z-orbitalerna lämnas orörda (figur 13.2).
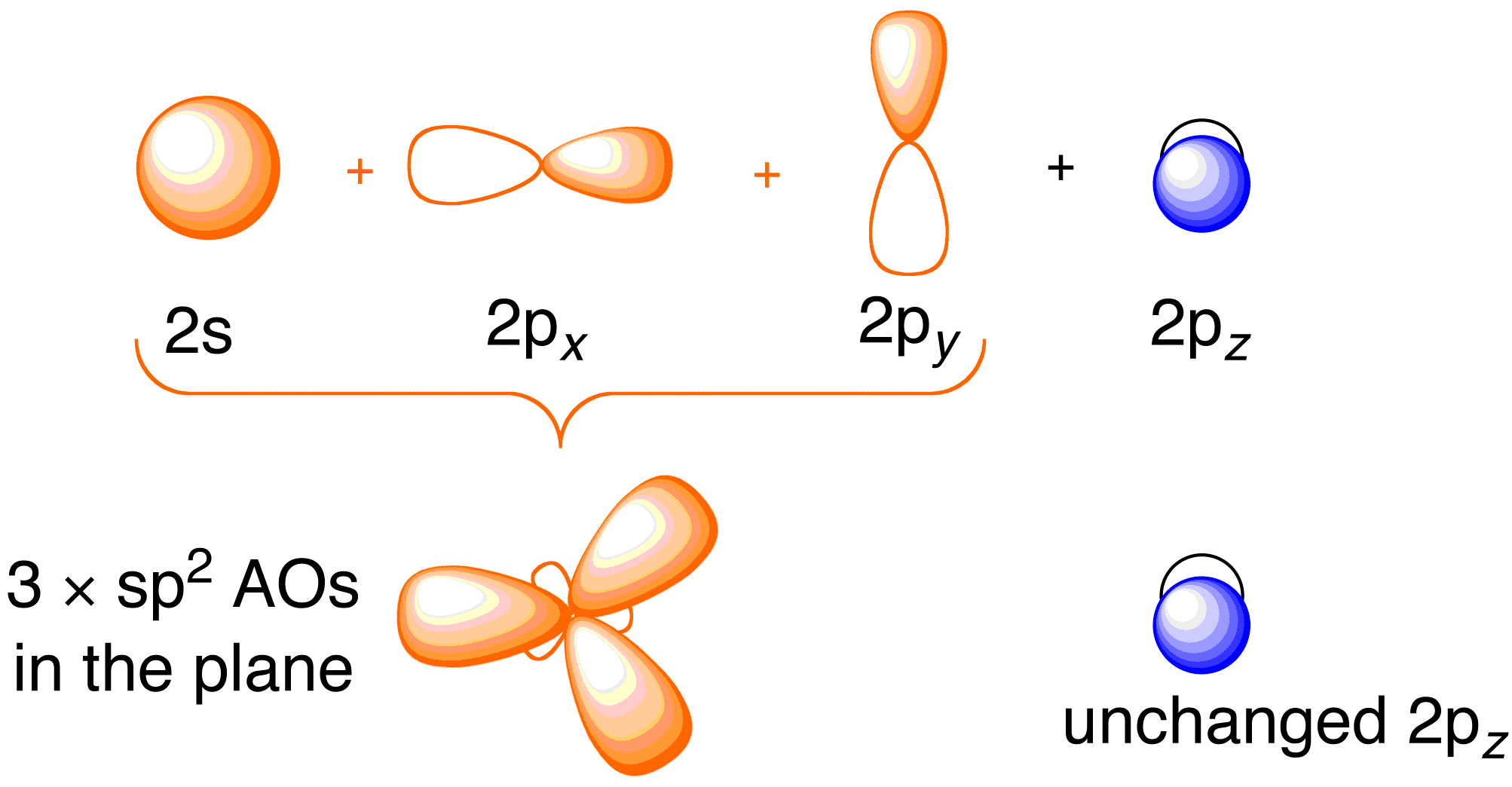
Figur 13.2. Hybridisering av kolatomorbitalerna för att ge sp^2 hybridorbitaler för bindning till väteatomer i eten. Bilden används med tillstånd från ChemTube (CC-SA-BY-NC; Nick Greeves).
Användningen av hybridorbitaler i den molekylära orbitala ansatsen som beskrivs här är endast en bekvämlighet och åberopar inte valensbindningsteorin (direkt). En identisk beskrivning kan utvinnas genom att enbart använda atomära orbitaler på kol, men tolkningen av de resulterande vågfunktionerna är mindre intuitiv. Exempelvis kan den i:e molekylära banan beskrivas via hybridorbitaler
\
eller via atomorbitaler.
\
där \{a_i\} och \{c_i\} är koefficienter för expansionen. Båda beskrivningarna fungerar och båda är identiska tillvägagångssätt eftersom
\
där \{c_i\} är koefficienter som beskriver den hybridiserade banan.
Bindningen sker via blandningen av elektronerna i sp^2-hybridorbitalerna på kol och elektronerna i 1satomorbitalerna hos de fyra väteatomerna (figur 13.2. ovan till vänster) vilket resulterar i \sigma -bindningsramen. \pi -bindningsramen är resultatet av de ohybridiserade 2p_z-orbitalerna (figur 13.2. ovan till höger). Oberoende av dessa två ramverk visas i det resulterande molekylära orbitaldiagrammet i figuren nedan; Hückel-teorin är endast inriktad på att beskriva molekylära orbitaler och energier för \pi-bindningsramverket.

Figur 13.3: Molekylära orbitaler som visar sigma-pi-separerbarheten hos \pi -bindningsramverket (blått) och \sigma -bindningsramverket (rött) för etylen.
Hückels behandling handlar endast om att beskriva molekylära orbitaler och energier för \pi-bindningsramen.
Då Hückel-teorin är en särskild betraktelse av molekylorbitalteorin kan molekylorbitalerna | \psi_i \rangle beskrivas som en linjär kombination av 2p_z-atomorbitalerna \phi vid kol med motsvarande \{c_i\}-koefficienter:
\\
För den fullständiga kvantkemiska analysen med Schrödingerekvationen (som inte krävs för kursen i organisk kemi), se denna Libretexts-sida.
Dessa molekylära orbitaler bildar π-bindningsramen och eftersom varje kol bidrar med en elektron till denna ram är endast den lägsta molekylära orbitalen ( | \psi_1 \rangle ) ockuperad (figur ) i grundtillståndet. Motsvarande elektronkonfiguration är då \pi_1^2 .

Figur 13.4: Schematisk representation av \pi-ramverket för molekylära orbitaler för etylen . Lägg märke till att den antibindande molekylorbitalen har en nod mer än den bindande molekylorbitalen, vilket är förväntat eftersom den har högre energi.
HOMO och LUMO är akronymer för högst ockuperad molekylorbital respektive lägst oockuperad molekylorbital, och kallas ofta för gränsorbitaler. Energidifferensen mellan HOMO och LUMO kallas HOMO-LUMO-gapet.
De 3-D beräknade \pi-molekylorbitalerna visas i figur 13.5.

Figur 13.5: Beräknade \pi-molekylorbitaler för etylen . (Till vänster) den bindande orbitalen (ψ1) och (till höger) den antibindande (ψ2) orbitalen.
Medarbetare
- Seymour Blinder (professor emeritus i kemi och fysik vid University of Michigan, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)
