En triangel med en rät vinkel kallas en rät triangel. Sidan mittemot den räta vinkeln kallas triangelns hypotenusa. De andra två sidorna kallas ben. De andra två vinklarna har inget särskilt namn, men de är alltid komplementära. Förstår du varför? Den totala vinkelsumman i en triangel är 180 grader, och den högra vinkeln är 90 grader, så de andra två måste summera till 90 grader.
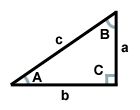
Triangeln ovan har sidan c som hypotenusa, sidorna a och b som ben och vinkeln C som rätvinkel. Vinklarna A och B är komplementära.
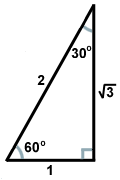
Det finns två typer av rätvinkliga trianglar som varje matematiker bör känna till mycket väl. Den ena är den rätvinkliga triangel som bildas när en höjd dras från ett hörn i en liksidig triangel och bildar två kongruenta rätvinkliga trianglar. Triangelns vinklar blir 30, 60 och 90 grader, vilket ger triangeln dess namn: 30-60-90 triangel. Förhållandet mellan sidlängderna i sådana trianglar är alltid detsamma: om benet mittemot den 30 graders vinkeln har längden x, kommer benet mittemot den 60 graders vinkeln att ha längden x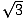
, och hypotenusan tvärs över den högra vinkeln kommer att vara 2x. Här är en 30-60-90 triangel avbildad nedan.
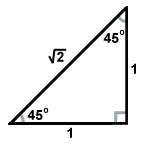
Den andra vanliga rätvinkliga triangeln är resultatet av det triangelpar som skapas när en diagonal delar en kvadrat i två trianglar. Var och en av dessa trianglar är kongruenta och har vinklar med måtten 45, 45 och 90 grader. Om benen mittemot de 45 graders vinklarna har längden x, har hypotenusan längden x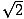
. Detta förhållande gäller för alla 45-45-90 trianglar. 45-45-90 trianglar kallas också ofta för likbenta rätvinkliga trianglar.
En sista egenskap att notera är att benen i en rätvinklig triangel också är triangelns höjder. Därför är arean av en rätvinklig triangel hälften av produkten av längderna av dess ben.