O resultado na análise de regressão logística é muitas vezes codificado como 0 ou 1, onde 1 indica que o resultado de interesse está presente, e 0 indica que o resultado de interesse está ausente. Se definirmos p como a probabilidade de que o resultado seja 1, o modelo de regressão logística múltipla pode ser escrito da seguinte forma:
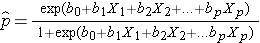
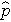é a probabilidade esperada de que o resultado esteja presente; X1 até Xp são variáveis independentes distintas; e b0 até bp são os coeficientes de regressão. O modelo de regressão logística múltipla é por vezes escrito de forma diferente. Na forma seguinte, o resultado é o log esperado das probabilidades de que o resultado está presente,
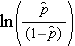
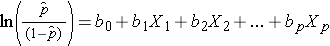
Notem que o lado direito da equação acima se parece com a equação de regressão linear múltipla. Entretanto, a técnica para estimar os coeficientes de regressão em um modelo de regressão logística é diferente daquela usada para estimar os coeficientes de regressão em um modelo de regressão linear múltipla. Na regressão logística os coeficientes derivados do modelo (por exemplo, b1) indicam a mudança nas probabilidades logísticas esperadas em relação a uma mudança de uma unidade em X1, mantendo constantes todos os outros preditores. Portanto, o antilog de um coeficiente de regressão estimado, exp(bi), produz uma odds ratio, como ilustrado no exemplo abaixo.
Exemplo de Regressão Logística – Associação entre Obesidade e CVD
Analizamos previamente dados de um estudo destinado a avaliar a associação entre obesidade (definida como IMC > 30) e doença cardiovascular incidente. Foram coletados dados de participantes com idade entre 35 e 65 anos, e livres de doenças cardiovasculares (DCV) na linha de base. Cada participante foi acompanhado durante 10 anos para o desenvolvimento de doenças cardiovasculares. Um resumo dos dados pode ser encontrado na página 2 deste módulo. O risco relativo não ajustado ou bruto foi RR = 1,78, e a razão de chances não ajustada ou bruta foi OR = 1,93. Também determinamos que a idade era um fator de confusão, e usando o método Cochran-Mantel-Haenszel, estimamos um risco relativo ajustado de RRCMH =1,44 e um odds ratio ajustado de ORCMH =1,52. Vamos agora usar a análise de regressão logística para avaliar a associação entre obesidade e doença cardiovascular incidente ajustada para a idade.
A análise de regressão logística revela o seguinte:
|
Variável Independente |
>
Coeficiente de Regressão |
>
Chi-quadrado |
Valor P |
|---|---|---|---|
| >
Interceptar |
>
-2.367 |
307.38 |
0.0001 |
|
Obesidade |
0,658 |
9,87> |
0.0017 |
O modelo de regressão logística simples relaciona a obesidade com as probabilidades logísticas de CVD incidentes:
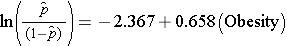
Obesidade é uma variável indicadora no modelo, codificada da seguinte forma 1=obeso e 0=não obeso. A probabilidade de registro de CVD incidente é 0,658 vezes maior em pessoas que são obesas do que não obesas. Se tomarmos a antilog do coeficiente de regressão, exp(0,658) = 1,93, obtemos a odds ratio bruta ou não ajustada. As probabilidades de desenvolvimento da DCV são 1,93 vezes maiores entre as pessoas obesas do que entre as não obesas. A associação entre obesidade e DCV incidente é estatisticamente significativa (p=0,0017). Observe que as estatísticas de teste para avaliar a significância dos parâmetros de regressão na análise de regressão logística são baseadas na estatística qui-quadrado, ao contrário das estatísticas t como foi o caso da análise de regressão linear. Isto porque uma técnica diferente de estimação, chamada estimativa de máxima verosimilhança, é usada para estimar os parâmetros da regressão (Veja Hosmer e Lemeshow3 para detalhes técnicos).
Muitos pacotes de computação estatística também geram odds ratios assim como intervalos de confiança de 95% para os odds ratios como parte do seu procedimento de análise de regressão logística. Neste exemplo, a estimativa do odds ratio é de 1,93 e o intervalo de confiança de 95% é (1,281, 2,913).
Quando examinamos a associação entre obesidade e DCV, determinamos anteriormente que a idade era um confundidor.O seguinte modelo de regressão logística múltipla estima a associação entre obesidade e DCV incidente, ajustando para a idade. No modelo consideramos novamente duas faixas etárias (menos de 50 anos de idade e 50 anos de idade e mais velhos). Para a análise, a faixa etária é codificada da seguinte forma: 1=50 anos de idade e mais velhos e 0=menos de 50 anos de idade.
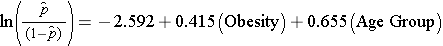
Se tomarmos o antilog do coeficiente de regressão associado à obesidade, exp(0,415) = 1,52 obtemos o odds ratio ajustado para a idade. As probabilidades de desenvolvimento de DCV são 1,52 vezes maiores entre obesos do que entre não obesos, ajustando-se para a idade. Na Seção 9.2 usamos o método Cochran-Mantel-Haenszel para gerar um odds ratio ajustado para a idade e encontramos o seguinte:
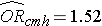
Isto ilustra como a análise de regressão logística múltipla pode ser usada para explicar a confusão. Os modelos podem ser estendidos para levar em conta várias variáveis de confusão simultaneamente. A análise de regressão logística múltipla também pode ser usada para avaliar a confusão e modificação de efeitos, e as abordagens são idênticas àquelas usadas na análise de regressão linear múltipla. A análise de regressão logística múltipla também pode ser usada para examinar o impacto de múltiplos fatores de risco (ao invés de focar em um único fator de risco) em um resultado dicotômico.
Exemplo – Fatores de risco associados ao baixo peso ao nascer do bebê
Suponha que os investigadores também estejam preocupados com resultados adversos da gravidez, incluindo diabetes gestacional, pré-eclâmpsia (ou seja, hipertensão induzida pela gravidez) e trabalho de parto pré-termo. Lembrar que o estudo envolveu 832 mulheres grávidas que fornecem dados demográficos e clínicos. Na amostra do estudo, 22 (2,7%) mulheres desenvolvem pré-eclâmpsia, 35 (4,2%) desenvolvem diabetes gestacional e 40 (4,8%) desenvolvem trabalho de parto pré-termo. Suponhamos que desejamos avaliar se existem diferenças em cada um desses resultados adversos da gravidez por raça/etnia, ajustados para a idade materna. Foram realizadas três análises de regressão logística distintas relacionando cada resultado, considerado separadamente, com as 3 variáveis dummy ou indicadores que refletem a raça materna e a idade materna, em anos. Os resultados são os seguintes.
|
Resultado: Pré-eclâmpsia |
Coeficiente de Regressão |
>
Chi-quadrado |
Valor P |
Rácio de Odds (95% CI) |
|---|---|---|---|---|
| >
Interceptar |
-3.066 |
4.518 |
0.0335 |
– |
| >
Preto raça |
2,191 |
12,640 |
0,0004 |
8.948 (2.673, 29.949) |
| >
Raça hispânica |
-0.1053 |
0.0325 |
0.8570 |
0.900 (0,286, 2,829) |
| >
Outra raça |
0,0586 |
0,0021 |
0.9046 |
1.060 (0.104, 3.698) |
|
Idade das mães (anos) |
-0.0252 |
0.3574 |
0,5500 |
0,975 (0,898, 1,059) |
A única diferença estatisticamente significativa na pré-eclâmpsia é entre as mães pretas e brancas.
As mães pretas têm quase 9 vezes mais probabilidade de desenvolver pré-eclâmpsia do que as mães brancas, ajustadas para a idade materna. O intervalo de confiança de 95% para a razão de chances comparando mulheres negras versus brancas que desenvolvem pré-eclâmpsia é muito amplo (2,673 a 29,949). Isto deve-se ao facto de haver um pequeno número de eventos de resultados (apenas 22 mulheres desenvolvem pré-eclâmpsia no total da amostra) e um pequeno número de mulheres de raça negra no estudo. Assim, esta associação deve ser interpretada com cautela.
Embora a odds ratio seja estatisticamente significativa, o intervalo de confiança sugere que a magnitude do efeito pode estar em qualquer lugar, desde um aumento de 2,6 vezes até um aumento de 29,9 vezes. Um estudo maior é necessário para gerar uma estimativa mais precisa do efeito.
|
Diabetes gestacional |
Coeficiente de regressão |
>
Chi-quadrado |
Valor P |
>
Razão de Odds (95% CI) |
|---|---|---|---|---|
| >
Interceptar |
-5.823 |
22,968 |
0,0001 |
– |
| >
Raça negra |
1,621 |
>
6.660 |
0,0099 |
5,056 (1.477, 17.312) |
|
Raça hispânica |
0,581 > |
1>1.766 |
0,1839 |
1,787 (0,759, 4,207) |
|
Outra raça |
1,348 |
5.917 |
0,0150 |
3,848 (1.299, 11.395) |
|
Idade da mãe (anos) |
0,071 |
4.314 |
0,0378 |
1,073 (1,004, 1,147) |
No que diz respeito à diabetes gestacional, existem diferenças estatisticamente significativas entre as mães negras e brancas (p=0,0099) e entre as mães que se identificam como outras raças em relação às brancas (p=0,0150), ajustadas à idade da mãe. A idade materna também é estatisticamente significativa (p=0,0378), sendo as mulheres mais velhas mais propensas a desenvolver diabetes gestacional, ajustada para raça/etnia.
|
Outcome: Trabalho Pré-termo |
Coeficiente de Regressão |
Chi-quadrado |
>
Valor P |
Rácio de Odds (95% CI) |
|---|---|---|---|---|
| >
Interceptar |
>
-1.443 |
1.602 |
0.2056 |
– |
| >
Preto raça |
-0.082 |
0.015 |
0.9039 |
0,921 (0,244, 3,483) |
|
Raça hispânica |
-1,564 |
9.497 |
0,0021 |
0,209 (0,077, 0,566) |
|
Outra raça |
0.548 |
1.124 |
0.2890 |
1.730 (0.628,4.767) |
| >
Idade da mãe (anos).) |
00,037 |
1,198 |
0,2737 |
0,963 (0,901, 1,030) |
>
Em relação ao trabalho de parto pré-termo, a única diferença estatisticamente significativa é entre mães hispânicas e brancas (p=0,0021). As mães hispânicas têm 80% menos probabilidade de desenvolver trabalho de parto pré-termo do que as mães brancas (odds ratio = 0,209), ajustado para a idade materna.
Métodos multivariáveis são computacionalmente complexos e geralmente requerem o uso de um pacote estatístico de computação. Métodos multivariados podem ser usados para avaliar e ajustar para confundir, para determinar se há efeito modificação, ou para avaliar as relações de vários fatores de exposição ou fatores de risco em um resultado simultaneamente. As análises multivariadas são complexas, e devem ser sempre planejadas para refletir relações biologicamente plausíveis. Embora seja relativamente fácil considerar uma variável adicional em um modelo de regressão linear múltipla ou logística múltipla, apenas variáveis que são clinicamente significativas devem ser incluídas.
É importante lembrar que modelos multivariados só podem ajustar ou considerar diferenças em variáveis confusas que foram medidas no estudo. Além disso, modelos multivariados só devem ser usados para contabilizar a confusão quando houver alguma sobreposição na distribuição do confundidor em cada um dos grupos de fatores de risco.
As análises estratificadas são muito informativas, mas se as amostras em estratos específicos forem muito pequenas, as análises podem carecer de precisão. Nos estudos de planejamento, os investigadores devem prestar atenção cuidadosa aos modificadores de efeitos potenciais. Se houver suspeita de que uma associação entre uma exposição ou fator de risco é diferente em grupos específicos, então o estudo deve ser projetado para garantir um número suficiente de participantes em cada um desses grupos. As fórmulas de tamanho de amostra devem ser usadas para determinar o número de sujeitos necessários em cada estrato para assegurar precisão ou potência adequada na análise.
voltar ao topo | página anterior | página seguinte